Part 2: Advanced Topics
Coding Patterns for Optimization Problems

In this chapter, we will explore various coding patterns that help you structure your implementations for optimization problems using CP-SAT. These patterns become especially useful when working on complex problems that need to be solved continuously and potentially under changing requirements. While we specifically focus on CP-SAT’s Python API, many patterns can be adapted to other solvers and languages.
In many cases, specifying the model and solving it is sufficient without the need for careful structuring. However, there are situations where your models are complex and require frequent iteration, either for performance reasons or due to changing requirements. In such cases, it is crucial to have a good structure in place to ensure that you can easily modify and extend your code without breaking it, as well as to facilitate testing and comprehension. Imagine you have a complex model and need to adapt a constraint due to new requirements. If your code is not modular and your test suite is only able to test the entire model, this small change will force you to rewrite all your tests. After a few iterations, you might end up skipping the tests altogether, which is a dangerous path to follow.
Another common issue in complex optimization models is the risk of forgetting to add some trivial constraints to interlink auxiliary variables, which can render parts of the model dysfunctional. If the dysfunctional part concerns feasibility, you might still notice it if you have separately checked the feasibility of the solution. However, if it involves the objective, such as penalizing certain combinations, you may not easily notice that your solution is suboptimal, as the penalties are not applied. Furthermore, implementing complex constraints can be challenging, and a modular structure allows you to test these constraints separately to ensure they work as intended. Test-driven development (TDD) is an effective approach for implementing complex constraints quickly and reliably.
The field of optimization is highly heterogeneous, and the percentage of optimizers with a professional software engineering background seems surprisingly low. Much of the optimization work is done by mathematicians, physicists, and engineers who have deep expertise in their fields but limited experience in software engineering. They are usually highly skilled and can create excellent models, but their code is often not very maintainable and does not follow software engineering best practices. Many problems are similar enough that minimal explanation or structure is deemed sufficient—much like creating plots by copying, pasting, and adjusting a familiar template. While this approach may not be very readable, it is familiar enough for most people in the field to understand. Additionally, it is typical for mathematicians to first document the model and then implement it. From a software engineering perspective, this workflow resembles the waterfall model, which lacks agility.
There appears to be a lack of literature on agile software development in optimization, which this chapter seeks to address by presenting some patterns I have found useful in my work. I asked a few senior colleagues in the field, and unfortunately, they could not provide any useful resources either or did not even see the need for such resources. For many use cases, the simple approach is indeed sufficient. However, I have found that these patterns make my agile, test-driven workflow much easier, faster, and more enjoyable. Note that this chapter is largely based on my personal experience due to the limited availability of references. I would be happy to hear about your experiences and the patterns you have found useful in your work.
In the following sections, we will start with the basic function-based pattern and then introduce further concepts and patterns that I have found valuable. We will work on simple examples where the benefits of these patterns may not be immediately apparent, but I hope you will see their potential in more complex problems. The alternative would have been to provide complex examples, which might have distracted from the patterns themselves.
 The following patterns focus on details specific to computational
optimization. However, many optimization engineers come from mathematics or
physics backgrounds and may not have professional Python or software
engineering experience. If you are among them, I recommend familiarizing
yourself in especially with
basic data structures and their comprehensions
and elegant loops using
itertools. These tools
allow you to express your mathematical ideas in Python more elegantly in
general, and they are especially useful for optimization problems.
Additionally, there are excellent tools to automatically format, check, and
improve your code, such as ruff.
Regularly running |
Simple Function
For straightforward optimization problems, encapsulating the model creation and solving within a single function is a practical approach. This method is best suited for simpler cases due to its straightforward nature but lacks flexibility for more complex scenarios. Parameters such as the time limit and optimality tolerance can be customized via keyword arguments with default values.
The following Python function demonstrates solving a simple knapsack problem using CP-SAT. To recap, in the knapsack problem, we select items - each with a specific weight and value - to maximize total value without exceeding a predefined weight limit. Given its simplicity, involving only one constraint, the knapsack problem serves as an ideal model for introductory examples.
from ortools.sat.python import cp_model
from typing import List
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*,
time_limit: int = 900,
opt_tol: float = 0.01,
) -> List[int]:
# initialize the model
model = cp_model.CpModel()
n = len(weights) # Number of items
# Decision variables for items
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
# Capacity constraint
model.add(sum(weights[i] * x[i] for i in range(n)) <= capacity)
# Objective function to maximize value
model.maximize(sum(values[i] * x[i] for i in range(n)))
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
status = solver.solve(model)
# Extract solution
return (
# Return indices of selected items
[i for i in range(n) if solver.value(x[i])]
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]
else []
)
You can also add some more flexibility by allowing any solver parameters to be passed to the solver.
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*,
time_limit: int = 900,
opt_tol: float = 0.01,
**kwargs,
) -> List[int]:
# initialize the model
model = cp_model.CpModel()
# ...
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
for key, value in kwargs.items():
setattr(solver.parameters, key, value)
# ...
Add some unit tests in some separate file (e.g., test_knapsack.py) to ensure
that the model works as expected.
 Write the tests before you write the code. This approach is known as test-driven development (TDD) and can help you to structure your code better and to ensure that your code works as expected. It also helps you to think about the API of your function before you start implementing it. |
# Make sure you have a proper project structure and can import your function
from myknapsacksolver import solve_knapsack
def test_knapsack_empty():
# Always good to have a test for the trivial case. The more trivial the
# case, the more likely it is that you forget it.
assert solve_knapsack([], [], 0) == []
def test_knapsack_nothing_fits():
# If nothing fits, we should get an empty solution
assert solve_knapsack([10, 20, 30], [1, 2, 3], 5) == []
def test_knapsack_one_item():
# If only one item fits, we should get this item
assert solve_knapsack([10, 20, 30], [1, 2, 3], 10) == [0]
def test_knapsack_all_items():
# If all items fit, we should get all items
assert solve_knapsack([10, 20, 30], [1, 2, 3], 100) == [0, 1, 2]
Using pytest, you can run all tests in the project with pytest .. Check
Real Python for a good tutorial
on pytest.
Logging the Model Building
When working with larger optimization problems, logging the model-building process can be essential to find and fix issues. Often, the problem lies not within the solver but in the model building itself.
In the following example, we add some basic logging to the solver function to give us some insights into the model-building process. This logging can be easily activated or deactivated by the logging framework, allowing us to use it not only during development but also in production, where you usually deactivate a lot of logging to save resources.
If you do not know about the logging framework of Python, this is an excellent
moment to learn about it. I consider it an essential skill for production code
and this and similar frameworks are used for most production code in any
language. The official Python documentation contains a
good tutorial. There are people
that prefer other logging frameworks, but it comes with Python and is good
enough for most use cases, definitely better than using the badly configurable
print statement.
import logging
from ortools.sat.python import cp_model
from typing import List
# Configure the logging framework if it is not already configured.
# We are setting it to debug level, as we are still developing the code.
logging.basicConfig(format="%(asctime)s - %(message)s", level=logging.DEBUG)
_logger = logging.getLogger(__name__) # get a logger for the current module
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*, # Make the following arguments keyword-only
time_limit: int = 900,
opt_tol: float = 0.01,
) -> List[int]:
_logger.debug("Building the knapsack model")
# initialize the model
model = cp_model.CpModel()
n = len(weights) # Number of items
_logger.debug("Number of items: %d", n)
if n > 0:
if _logger.isEnabledFor(logging.DEBUG):
# Only calculate min, mean, and max if we actually log it
_logger.debug(
"Min/Mean/Max weight: %d/%.2f/%d",
min(weights),
sum(weights) / n,
max(weights),
)
_logger.debug(
"Min/Mean/Max value: %d/%.2f/%d", min(values), sum(values) / n, max(values)
)
# Decision variables for items
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
# Capacity constraint
model.add(sum(weights[i] * x[i] for i in range(n)) <= capacity)
# Objective function to maximize value
model.maximize(sum(values[i] * x[i] for i in range(n)))
# Log the model
_logger.debug("Model created with %d items", n)
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
_logger.debug(
"Starting the solution process with time limit %d seconds", time_limit
)
status = solver.solve(model)
# Extract solution
selected_items = (
[i for i in range(n) if solver.value(x[i])]
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]
else []
)
_logger.debug("Selected items: %s", selected_items)
return selected_items
We will not use logging in the following examples to save space, but you should consider adding it to your code.
 A great hack you can do with the logging framework is that you can easily hook
into your code and do analysis beyond the simple logging. You can simply write
a handler that, e.g., waits for the tag |
Custom Data Classes for Instances, Configurations, and Solutions
Incorporating serializable data classes based on strict schema to manage instances, configurations, and solutions significantly enhances code readability and maintainability. These classes also facilitate documentation, testing, and ensure data consistency across larger projects where data exchange among different components is necessary.
One popular library for this purpose is Pydantic. It is easy to use and provides substantial functionality out of the box. The following code introduces data classes for the instance, configuration, and solution of the knapsack problem. While Python’s duck typing is great for rapidly developing internal data flow, it can be problematic for interfaces. Users will often misuse the interface in unexpected ways, and you will be blamed for it. Pydantic helps mitigate these issues by providing a clear interface and validating input data. Additionally, you can create an API for your code effortlessly using FastAPI, which is built on top of Pydantic.
# pip install pydantic
from pydantic import (
BaseModel,
PositiveInt,
NonNegativeFloat,
PositiveFloat,
Field,
model_validator,
)
class KnapsackInstance(BaseModel):
# Defines the knapsack instance to be solved.
weights: list[PositiveInt] = Field(..., description="The weight of each item.")
values: list[PositiveInt] = Field(..., description="The value of each item.")
capacity: PositiveInt = Field(..., description="The capacity of the knapsack.")
@model_validator(mode="after")
def check_lengths(cls, v):
if len(v.weights) != len(v.values):
raise ValueError("Mismatch in number of weights and values.")
return v
class KnapsackSolverConfig(BaseModel):
# Defines the configuration for the knapsack solver.
time_limit: PositiveFloat = Field(
default=900.0, description="Time limit in seconds."
)
opt_tol: NonNegativeFloat = Field(
default=0.01, description="Optimality tolerance (1% gap allowed)."
)
log_search_progress: bool = Field(
default=False, description="Whether to log the search progress."
)
class KnapsackSolution(BaseModel):
# Defines the solution of the knapsack problem.
selected_items: list[int] = Field(..., description="Indices of selected items.")
objective: float = Field(..., description="Objective value of the solution.")
upper_bound: float = Field(
..., description="Upper bound of the solution, i.e., a proven limit on how good a solution could be."
)
 Your data schema should be fully prepared for the optimization process, requiring no further preprocessing. Data preparation and optimization are both complex tasks, and combining them can significantly increase complexity, making your code difficult to maintain. Ideally, your optimization code should simply iterate over the data and add the corresponding constraints and objectives to the model. |
The original code needs to be adapted to use these data classes.
from ortools.sat.python import cp_model
def solve_knapsack(
instance: KnapsackInstance, config: KnapsackSolverConfig
) -> KnapsackSolution:
model = cp_model.CpModel()
n = len(instance.weights)
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
model.add(sum(instance.weights[i] * x[i] for i in range(n)) <= instance.capacity)
model.maximize(sum(instance.values[i] * x[i] for i in range(n)))
solver = cp_model.CpSolver()
# Set solver parameters from the configuration
solver.parameters.max_time_in_seconds = config.time_limit
solver.parameters.relative_gap_limit = config.opt_tol
solver.parameters.log_search_progress = config.log_search_progress
# Solve the model and return the solution
status = solver.solve(model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=[i for i in range(n) if solver.value(x[i])],
objective=solver.objective_value,
upper_bound=solver.best_objective_bound,
)
return KnapsackSolution(selected_items=[], objective=0, upper_bound=0)
You can use the serialization and deserialization capabilities of Pydantic to quickly generate test cases based on real data. While you cannot be certain that your code is correct with such tests, they will at least notify you if the logic changes unexpectedly. If you refactor your code, you will immediately see if its behavior changes accidentally.
from datetime import datetime
from hashlib import md5
from pathlib import Path
def add_test_case(instance: KnapsackInstance, config: KnapsackSolverConfig):
"""
Quickly generate a test case based on the instance and configuration.
"""
test_folder = Path(__file__).parent / "test_data"
unique_id = (
datetime.now().strftime("%Y-%m-%d-%H-%M-%S")
+ "_"
+ md5(
(instance.model_dump_json() + config.model_dump_json()).encode()
).hexdigest()
)
subfolder = test_folder / "knapsack" / unique_id
subfolder.mkdir(parents=True, exist_ok=True)
with open(subfolder / "instance.json", "w") as f:
f.write(instance.model_dump_json())
with open(subfolder / "config.json", "w") as f:
f.write(config.model_dump_json())
solution = solve_knapsack(instance, config)
with open(subfolder / "solution.json", "w") as f:
f.write(solution.model_dump_json())
def test_saved_test_cases():
test_folder = Path(__file__).parent / "test_data"
for subfolder in test_folder.glob("knapsack/*"):
with open(subfolder / "instance.json") as f:
instance = KnapsackInstance.model_validate_json(f.read())
with open(subfolder / "config.json") as f:
config = KnapsackSolverConfig.model_validate_json(f.read())
with open(subfolder / "solution.json") as f:
solution = KnapsackSolution.model_validate_json(f.read())
new_solution = solve_knapsack(instance, config)
assert (
new_solution.objective <= solution.upper_bound
), "New solution is better than the previous upper bound: One has to be wrong."
assert (
solution.objective <= new_solution.upper_bound
), "Old solution is better than the new upper bound: One has to be wrong."
# Do not test for the selected items, as the solver might return a different solution of the same quality
You can now easily generate test cases and validate them with the following code. Ideally, you should use real instances for this, potentially by automatically saving 1% of the instances used in production.
# Define a knapsack instance
instance = KnapsackInstance(
weights=[23, 31, 29, 44, 53, 38, 63, 85, 89, 82],
values=[92, 57, 49, 68, 60, 43, 67, 84, 87, 72],
capacity=165,
)
# Define a solver configuration
config = KnapsackSolverConfig(
time_limit=10.0, opt_tol=0.01, log_search_progress=False
)
# Solve the knapsack problem
solution = solve_knapsack(instance, config)
# Add the test case to the test data folder
add_test_case(instance, config)
You can also maintain backward compatibility easily by adding default values to any new fields you add to the data classes.
 One challenge I often face is designing data classes to be as generic as possible so that they can be used with multiple solvers and remain compatible throughout various stages of the optimization process. For instance, a graph might be represented as an edge list, an adjacency matrix, or an adjacency list, each with its own pros and cons, complicating the decision of which format is optimal for all stages. However, converting between different data class formats is typically straightforward, often requiring only a few lines of code and having a negligible impact compared to the optimization process itself. Therefore, I recommend focusing on functionality with your current solver without overcomplicating this aspect. There is little harm in having to call a few conversion functions because you created separate specialized data classes. |
Solver Class
In many real-world optimization scenarios, problems may require iterative refinement of the model and solution. For instance, new constraints might only become apparent after presenting an initial solution to a user or another algorithm (like a physics simulation, which is to complex to optimize directly on). In such cases, flexibility is crucial, making it beneficial to encapsulate both the model and the solver within a single class. This setup facilitates the dynamic addition of constraints and subsequent re-solving without needing to rebuild the entire model, potentially even utilizing warm-starting techniques to improve performance.
We introduce the KnapsackSolver class, which encapsulates the entire setup and
solving process of the knapsack problem. We also use the opportunity to directly
split the model-building into smaller methods, which can be useful for more
complex models.
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self.n = len(instance.weights)
self.x = [self.model.new_bool_var(f"x_{i}") for i in range(self.n)]
self._build_model()
self.solver = cp_model.CpSolver()
def _add_constraints(self):
used_weight = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.add(used_weight <= self.instance.capacity)
def _add_objective(self):
self.model.maximize(
sum(value * x_i for value, x_i in zip(self.instance.values, self.x))
)
def _build_model(self):
self._add_constraints()
self._add_objective()
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def prohibit_combination(self, item_a: int, item_b: int):
"""
Prohibit the combination of two items in the solution.
This can be useful if, after presenting the solution to the user, they decide that these two items should not be packed together. After calling this method, you can simply call `solve` again to get a new solution obeying this constraint.
"""
self.model.add(self.x[item_a] + self.x[item_b] <= 1)
At first glance, this may look like a cumbersome interface, as we first have to
create a solver object for a specific instance and then call the solve method.
However, this structure accommodates many use cases, and I use variations of it
for most of my projects. Additionally, I sometimes add a simple function that
wraps the solver class to make it easier to use for simple cases.
instance = KnapsackInstance(weights=[1, 2, 3], values=[4, 5, 6], capacity=3)
config = KnapsackSolverConfig(time_limit=10, opt_tol=0.01, log_search_progress=True)
solver = KnapsackSolver(instance, config)
solution = solver.solve()
print(solution)
# Check the solution in a more realistic simulation.
# Assume that the simulation now notices that for some more complex reason,
# we could not express in the optimization model, the first two items should
# not be packed together. We can now prohibit this combination and solve again.
solver.prohibit_combination(0, 1)
# Solve the problem again with the new constraint, but this time
# only allow 5 seconds for the solver.
solution = solver.solve(time_limit=5)
print(solution)
Although reusing the solver class primarily spares us from rebuilding the model,
each call to solve still initiates a new search from scratch. However,
iteratively refining the model within the same solver instance is more intuitive
to code than treating each iteration as an entirely new problem. Moreover, as we
will demonstrate next, this pattern allows us to improve performance by
leveraging features like warm-starting — offering advantages over stateless
optimization functions.
Improving Performance with Warm-Starts
As the solver class retains a state and can remember the previous iterations, we can easily add optimizations that would be cumbersome to implement in a stateless function. One such optimization is warm-starting, where the solver uses the previous solution as a starting point or “hint” for the next iteration. This technique can significantly speed up the solving process, as the solver can often use the previous solution as a good starting point for repair, even if the previous solution becomes infeasible due to a newly added constraint. This will of course only have an advantage if the added constraint does not change the problem fundamentally but only requires a part of the solution to be changed.
Because repairing an infeasible hint can be computationally expensive, CP-SAT
handles this process carefully. You can instruct CP-SAT to attempt repairing the
hint by setting solver.parameters.repair_hint = True. Additionally, you can
adjust the limit on how much effort CP-SAT should spend repairing the hint using
solver.parameters.hint_conflict_limit. For example, setting
solver.parameters.hint_conflict_limit = 10 controls how many conflicts CP-SAT
will resolve before giving up.
Here is an example of how to implement this in code:
class KnapsackSolver:
# ...
def _set_solution_as_hint(self):
"""Use the current solution as a hint for the next solve."""
for i, v in enumerate(self.model.proto.variables):
v_ = self.model.get_int_var_from_proto_index(i)
assert v.name == v_.name, "Variable names should match"
self.model.add_hint(v_, self.solver.value(v_))
# Tell CP-SAT to repair the hint if it is infeasible
self.solver.parameters.repair_hint = True
self.solver.parameters.hint_conflict_limit = 20
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
# There is a solution, set it as a hint for the next solve
self._set_solution_as_hint()
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
# ...
To further improve this approach, you could add a heuristic to repair the hint. A feasible hint is much more valuable than one that needs significant repair. For instance, if the hint is infeasible due to a prohibited combination of items, you could simply drop the least valuable item to make the hint valid.
 A common mistake when trying to improve the performance of iterative optimization is adding the previous bound as a constraint. Although this approach might let CP-SAT resume directly from the previous bound, it often limits CP-SAT’s ability to find better solutions. This happens because it adds a strong constraint unrelated to the problem’s feasibility, which can interfere with various internal algorithms (such as reducing the effectiveness of linear relaxation). If bounds significantly affect performance, consider using a callback to check if the current objective is sufficiently close to the previous bound and stop the search if it is. This approach avoids interfering with CP-SAT’s optimization capabilities, though callbacks do introduce some overhead. |
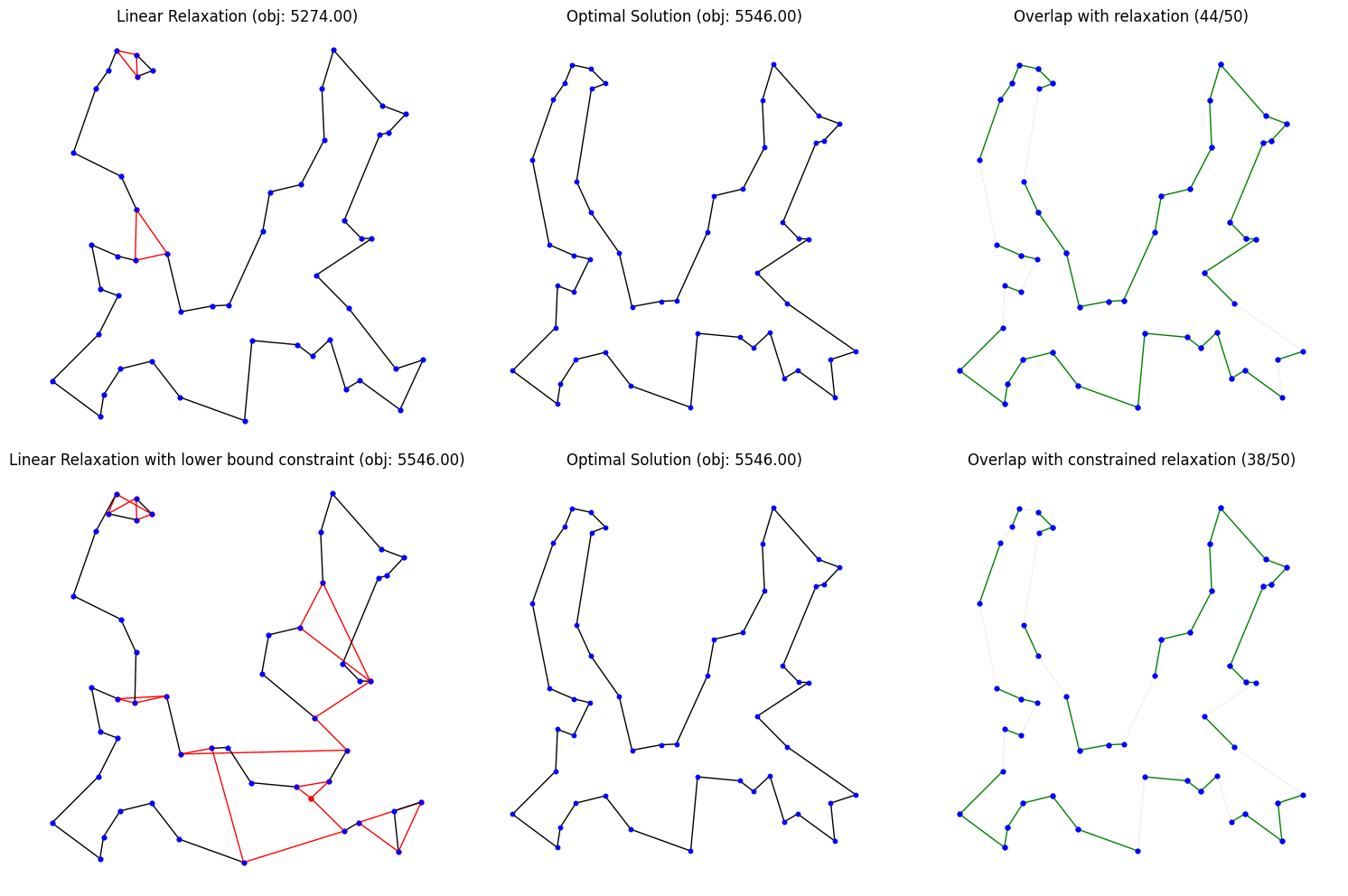 |
|---|
| This image illustrates the detrimental impact of introducing a lower bound constraint into the model on the example of the TSP. The linear relaxation visibly deteriorates: while the original relaxation coincided with the optimal solution on 44 of 50 edges, the relaxation incorporating the lower bound constraint (set to the optimal value) coincides on only 38 edges and exhibits significantly more fractional values. Branching on certain edges may also cease to provide meaningful guidance; unless one branches on a poorly chosen edge, the objective value often remains unchanged as it is dominated by the lower bound constraint. In addition to the reduced informational value of the relaxation, such constraints are also notorious for introducing numerical instabilities (however, CP-SAT is likely unaffected by this issue due to its reliance on integer arithmetic). |
Exchangeable Objective / Multi-Objective Optimization
In real-world scenarios, objectives are often not clearly defined. Typically, there are multiple objectives with different priorities, making it challenging to combine them. Consider the Knapsack problem, representing a logistics issue where we aim to transport the maximum value of goods in a single trip. Given the values and weights of the goods, our primary objective is to maximize the packed goods’ value. However, after computing and presenting the solution, we might be asked to find an alternative solution that does not fill the truck as much, even if it means accepting up to a 5% decrease in value.
 |
|---|
| Which fruit is the best one? Many problems are multi-objective and there is no clear single objective. By xkcd (CC BY-NC 2.5) |
To handle this, we can optimize in two phases. First, we maximize the value under the weight constraint. Next, we add a constraint that the value must be at least 95% of the initial solution’s value and change the objective to minimize the weight. This iterative process can continue through multiple phases, exploring the Pareto front of the two objectives. More complex problems can be tackled using similar approaches.
A challenge with this method is avoiding the creation of multiple models and restarting from scratch in each phase. Since we have a solution close to the new one and changing the objective does not influence feasibility, it is an excellent opportunity to use the current solution as a hint for the next solve.
The following code demonstrates how to extend a solver class to support exchangeable objectives. It includes fixing the current objective value to prevent degeneration and using the current solution as a hint.
We created a member _objective to store the current objective function and
added methods to set the objective to maximize value or minimize weight. We also
introduced methods to set the solution as a hint for the next solve which will
automatically be called if the solve found a feasible solution. To not
degenerate on previous objectives, we added a method to fix the current
objective value based on some ratio.
class MultiObjectiveKnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self.n = len(instance.weights)
self.x = [self.model.new_bool_var(f"x_{i}") for i in range(self.n)]
self._objective = 0
self._build_model()
self.solver = cp_model.CpSolver()
def set_maximize_value_objective(self):
"""Set the objective to maximize the value of the packed goods."""
self._objective = sum(
value * x_i for value, x_i in zip(self.instance.values, self.x)
)
self.model.maximize(self._objective)
def set_minimize_weight_objective(self):
"""Set the objective to minimize the weight of the packed goods."""
self._objective = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.minimize(self._objective)
def _set_solution_as_hint(self):
"""Use the current solution as a hint for the next solve."""
for i, v in enumerate(self.model.proto.variables):
v_ = self.model.get_int_var_from_proto_index(i)
assert v.name == v_.name, "Variable names should match"
self.model.add_hint(v_, self.solver.value(v_))
def fix_current_objective(self, ratio: float = 1.0):
"""Fix the current objective value to prevent degeneration."""
if ratio == 1.0:
self.model.add(self._objective == self.solver.objective_value)
elif ratio > 1.0:
self.model.add(self._objective <= ceil(self.solver.objective_value * ratio))
else:
self.model.add(
self._objective >= floor(self.solver.objective_value * ratio)
)
def _add_constraints(self):
"""Add the weight constraint to the model."""
used_weight = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.add(used_weight <= self.instance.capacity)
def _build_model(self):
"""Build the initial model with constraints and objective."""
self._add_constraints()
self.set_maximize_value_objective()
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
"""Solve the knapsack problem and return the solution."""
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
self._set_solution_as_hint()
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
We can use the MultiObjectiveKnapsackSolver class as follows:
config = KnapsackSolverConfig(time_limit=15, opt_tol=0.01, log_search_progress=True)
solver = MultiObjectiveKnapsackSolver(instance, config)
solution_1 = solver.solve()
# maintain at least 95% of the current objective value
solver.fix_current_objective(0.95)
# change the objective to minimize the weight
solver.set_minimize_weight_objective()
solution_2 = solver.solve(time_limit=10)
There are more advanced and precise methods for computing the Pareto front, but multi-objective optimization is a complex field of research in its own right. If your problem is already challenging with a single objective, adding more objectives will only increase the difficulty.
Using the shown approach of lexicographic optimization (with relaxation) or combining multiple objectives into a single one, for example by adding them with different weights, is often a reasonable compromise. You could also use heuristics to explore the solution space around an initial solution obtained with CP-SAT.
However, multi-objective optimization remains a challenging topic, and even experts rely on significant trial and error to achieve satisfactory results, as compromises are often unavoidable.
Variable Containers
In complex models, variables play a crucial role and can span the entire model. While managing variables as a list or dictionary may suffice for simple models, this approach becomes cumbersome and error-prone as the model’s complexity increases. A single mistake in indexing can introduce subtle errors, potentially leading to incorrect results that are difficult to trace.
As variables form the foundation of the model, refactoring them becomes more challenging as the model grows. Therefore, it is crucial to establish a robust management system early on. Encapsulating variables in a dedicated class ensures that they are always accessed correctly. This approach also allows for the easy addition of new variables or modifications in their management without altering the entire model.
Furthermore, incorporating clear query methods helps maintain the readability and manageability of constraints. Readable constraints, free from complex variable access patterns, ensure that the constraints accurately reflect the intended model.
In the following code, we introduce the _ItemSelectionVars class to the
KnapsackSolver, which acts as a container for the decision variables
associated with the knapsack items. This class not only creates these variables
but also offers several utility methods to interact with them, improving the
clarity and maintainability of the code.
from typing import Generator, Tuple, List
class _ItemSelectionVars:
def __init__(self, instance: KnapsackInstance, model: cp_model.CpModel, var_name: str = "x"):
self.instance = instance
self.x = [model.new_bool_var(f"{var_name}_{i}") for i in range(len(instance.weights))]
def __getitem__(self, i: int) -> cp_model.IntVar:
return self.x[i]
def packs_item(self, i: int) -> cp_model.IntVar:
return self.x[i]
def extract_packed_items(self, solver: cp_model.CpSolver) -> List[int]:
return [i for i, x_i in enumerate(self.x) if solver.value(x_i)]
def used_weight(self) -> cp_model.LinearExprT:
return sum(weight * x_i for weight, x_i in zip(self.instance.weights, self.x))
def packed_value(self) -> cp_model.LinearExprT:
return sum(value * x_i for value, x_i in zip(self.instance.values, self.x))
def iter_items(
self,
weight_lb: float = 0.0,
weight_ub: float = float("inf"),
value_lb: float = 0.0,
value_ub: float = float("inf"),
) -> Generator[Tuple[int, cp_model.IntVar], None, None]:
"""
An example for a more complex query method, which would allow use to
iterate over all items that fulfill certain conditions.
"""
for i, (weight, x_i) in enumerate(zip(self.instance.weights, self.x)):
if (
weight_lb <= weight <= weight_ub
and value_lb <= self.instance.values[i] <= value_ub
):
yield i, x_i
This class can be used in the KnapsackSolver that handles the higher level
logic, i.e., the high level specification of what the model should do, while
details can be hidden in the container class.
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self._item_vars = _ItemSelectionVars(instance, self.model)
self._build_model()
self.solver = cp_model.CpSolver()
def _add_constraints(self):
self.model.add(self._item_vars.used_weight() <= self.instance.capacity)
def _add_objective(self):
self.model.maximize(self._item_vars.packed_value())
def _build_model(self):
self._add_constraints()
self._add_objective()
def solve(self) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=self._item_vars.extract_packed_items(self.solver),
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def prohibit_combination(self, item_a: int, item_b: int):
self.model.add_at_most_one(self._item_vars.packs_item(item_a),
self._item_vars.packs_item(item_b))
For example,
self.model.add(self._item_vars.used_weight() <= self.instance.capacity) now
directly expresses what the constraint does, making the code more readable and
less error-prone. You can actually hide additional optimizations in the
container class, without influencing the higher-level code in the actual solver.
For example, the container class could decide to automatically replace all item
variables that cannot fit into the knapsack due to their weight with a constant.
You can also reuse the variable type, e.g., if you suddenly have two knapsacks to fill. The following code demonstrates how to quickly extend the solver to handle two knapsacks, without sacrificing readability or maintainability.
class KnapsackSolver:
def __init__(self, # ...
):
#...
self._knapsack_a = _ItemSelectionVars(instance, self.model, var_name="x1")
self._knapsack_b = _ItemSelectionVars(instance, self.model, var_name="x2")
#...
def _add_constraints(self):
self.model.add(self._knapsack_a.used_weight() <= self.instance.capacity_1)
self.model.add(self._knapsack_b.used_weight() <= self.instance.capacity_2)
self.model.add(self._knapsack_a.used_weight() + self._knapsack_b.used_weight() <= self.instance.capacity_total)
# Add a constraint that items cannot be packed in both knapsacks
for i in range(len(instance.weights)):
self.model.add_at_most_one(self._knapsack_a.packs_item(i), self._knapsack_b.packs_item(i))
def _add_objective(self):
self.model.maximize(self._knapsack_a.packed_value() + self._knapsack_b.packed_value())
 Do not create such a container class for simple models where the container would only wrap a list or a dictionary without adding any additional functionality. In such cases, directly using the list or dictionary is preferable, as it is more concise and easier to understand. The same is true for individual variables that do not need a container at all. |
Lazy Variable Construction
In models with numerous auxiliary variables, often only a subset is actually used by the constraints. Attempting to create only the variables that are needed can require complex code to ensure that exactly the right variables are generated. If the model is extended later, this process becomes even more complicated, as you may not know upfront which variables will be needed. This is where lazy variable construction comes into play. By creating variables only when they are accessed, we ensure that only necessary variables are generated, reducing memory usage and computational overhead. While this approach might be more expensive if most variables end up being used anyway, it can save significant resources when only a small subset is actually needed.
To illustrate this concept, we introduce the _CombiVariables class. This class
manages auxiliary variables that indicate when a pair of items is packed
together, allowing us to assign additional bonuses for packing certain items
together. Theoretically, the number of possible item combinations is quadratic
in the number of items, but in practice, only a few may be relevant. By creating
these variables lazily—only when they are accessed—we reduce memory usage and
computational overhead.
class _CombiVariables:
def __init__(
self,
instance: KnapsackInstance,
model: cp_model.CpModel,
item_vars: _ItemSelectionVars,
):
self.instance = instance
self.model = model
self.item_vars = item_vars
self.bonus_vars = {}
def __getitem__(self, item_pair: Tuple[int, int]) -> cp_model.IntVar:
i, j = sorted(item_pair)
if (i, j) not in self.bonus_vars:
var = self.model.NewBoolVar(f"bonus_{i}_{j}")
self.model.add(
self.item_vars.packs_item(i) + self.item_vars.packs_item(j) >= 2 * var
)
self.bonus_vars[(i, j)] = var
return self.bonus_vars[(i, j)]
In the KnapsackSolver, we can now treat these variables as if they were all
pre-created, without worrying about the underlying optimization. Note that we
have moved the creation of the objective function into the solve method, as
adding bonuses for item combinations will modify the objective function. Also,
by encapsulating item variables into a separate class (_ItemSelectionVars), we
can easily pass them around and use them in other components.
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self._item_vars = _ItemSelectionVars(instance, self.model)
self._bonus_vars = _CombiVariables(instance, self.model, self._item_vars)
self._objective_terms = [self._item_vars.packed_value()] # Initial objective terms
self.solver = cp_model.CpSolver()
def solve(self) -> KnapsackSolution:
self.model.maximize(sum(self._objective_terms))
self.solver.parameters.max_time_in_seconds = self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=self._item_vars.extract_packed_items(self.solver),
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def add_bonus(self, item_a: int, item_b: int, bonus: int):
bonus_var = self._bonus_vars[(item_a, item_b)]
self._objective_terms.append(bonus * bonus_var)
 If we are sure to only call |
Submodels
We can further enhance our modeling approach by encapsulating entire sections of the model—not just individual variables—into separate submodels. This technique is particularly useful for complex models where different components are loosely connected. By partitioning the model into smaller, more manageable submodels, we improve modularity and maintainability. Submodels communicate with the main model through shared variables, effectively hiding internal details like auxiliary variables. If requirements change, we can often reconfigure or replace specific submodels without affecting the rest of the model. In larger contexts, it is also common for logic to repeat in different optimization problems of the system, so building a collection of submodels allows us to quickly assemble new models using reusable components.
For instance, piecewise linear functions can be modeled as submodels, as
demonstrated with the PiecewiseLinearConstraint class in
piecewise_linear_function.py.
Each submodel handles a piecewise linear function independently, interfacing
with the main model through shared x and y variables. By encapsulating the
logic for each piecewise function in a dedicated class, we make it reusable and
testable in isolation.
from ortools.sat.python import cp_model
requirements_1 = (3, 5, 2)
requirements_2 = (2, 1, 3)
model = cp_model.CpModel()
buy_1 = model.new_int_var(0, 1_500, "buy_1")
buy_2 = model.new_int_var(0, 1_500, "buy_2")
buy_3 = model.new_int_var(0, 1_500, "buy_3")
produce_1 = model.new_int_var(0, 300, "produce_1")
produce_2 = model.new_int_var(0, 300, "produce_2")
model.add(produce_1 * requirements_1[0] + produce_2 * requirements_2[0] <= buy_1)
model.add(produce_1 * requirements_1[1] + produce_2 * requirements_2[1] <= buy_2)
model.add(produce_1 * requirements_1[2] + produce_2 * requirements_2[2] <= buy_3)
# You can find the PiecewiseLinearFunction and PiecewiseLinearConstraint classes in the utils directory
from piecewise_functions import PiecewiseLinearFunction, PiecewiseLinearConstraint
# Define the functions for the costs
costs_1 = [(0, 0), (1000, 400), (1500, 1300)]
costs_2 = [(0, 0), (300, 300), (700, 500), (1200, 600), (1500, 1100)]
costs_3 = [(0, 0), (200, 400), (500, 700), (1000, 900), (1500, 1500)]
f_costs_1 = PiecewiseLinearFunction(
xs=[x for x, y in costs_1], ys=[y for x, y in costs_1]
)
f_costs_2 = PiecewiseLinearFunction(
xs=[x for x, y in costs_2], ys=[y for x, y in costs_2]
)
f_costs_3 = PiecewiseLinearFunction(
xs=[x for x, y in costs_3], ys=[y for x, y in costs_3]
)
# Define the functions for the gains
gain_1 = [(0, 0), (100, 800), (200, 1600), (300, 2000)]
gain_2 = [(0, 0), (80, 1000), (150, 1300), (200, 1400), (300, 1500)]
f_gain_1 = PiecewiseLinearFunction(
xs=[x for x, y in gain_1], ys=[y for x, y in gain_1]
)
f_gain_2 = PiecewiseLinearFunction(
xs=[x for x, y in gain_2], ys=[y for x, y in gain_2]
)
# Create y >= f(x) constraints for the costs
x_costs_1 = PiecewiseLinearConstraint(model, buy_1, f_costs_1, upper_bound=False)
x_costs_2 = PiecewiseLinearConstraint(model, buy_2, f_costs_2, upper_bound=False)
x_costs_3 = PiecewiseLinearConstraint(model, buy_3, f_costs_3, upper_bound=False)
# Create y <= f(x) constraints for the gains
x_gain_1 = PiecewiseLinearConstraint(model, produce_1, f_gain_1, upper_bound=True)
x_gain_2 = PiecewiseLinearConstraint(model, produce_2, f_gain_2, upper_bound=True)
# Maximize the gains minus the costs
model.maximize(x_gain_1.y + x_gain_2.y - (x_costs_1.y + x_costs_2.y + x_costs_3.y))
Testing complex optimization models is often challenging because outputs can be sensitive to small changes in the model. Even with a good test case, detected errors may be difficult to trace. By extracting elements into submodels, you can test these submodels independently, ensuring they work correctly before integrating them into the main model.
Submodels are usually much simpler than the overall problem, making them easy to optimize and, thus, fast to test their optimal solution.
from ortools.sat.python import cp_model
def test_piecewise_linear_upper_bound_constraint():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
# Using the submodel
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
model.maximize(c.y)
# Checking its behavior
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.OPTIMAL
assert solver.value(c.y) == 10
assert solver.value(x) == 10
Alternatively, testing for feasibility or infeasibility can be a good choice, especially if the submodel does not directly correspond to an optimization problem on its own.
from ortools.sat.python import cp_model
def test_piecewise_linear_upper_bound_constraint_via_fixation():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
# Fix the variables to specific values
model.add(x == 10)
model.add(c.y == 10)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.OPTIMAL, "The model should be feasible"
def test_piecewise_linear_upper_bound_constraint_via_fixation_infeasible():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
# Fix the variables to specific values that violate the constraint
model.add(x == 10)
model.add(c.y == 11)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.INFEASIBLE, "The model should be infeasible"
Embedding CP-SAT in an Application via multiprocessing
If you want to embed CP-SAT in your application for potentially long-running optimization tasks, you can utilize callbacks to provide users with progress updates and potentially interrupt the process early. However, one issue is that the application can only react during the callback. Since the callback is not always called frequently, this may lead to problematic delays, making it unsuitable for graphical user interfaces (GUIs) or application programming interfaces (APIs).
An alternative is to let the solver run in a separate process and communicate with it using a pipe. This approach allows the solver to be interrupted at any time, enabling the application to react immediately. Python’s multiprocessing module provides reasonably simple ways to achieve this. This example showcases such an approach. However, for scaling this approach up, you will actually have to build a task queues where the solver is run by workers. Using multiprocessing can still be useful for the worker to remain responsive for stop signals while the solver is running.
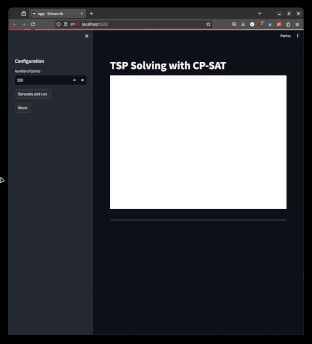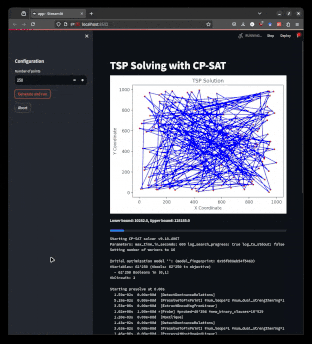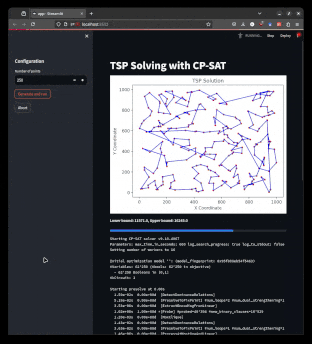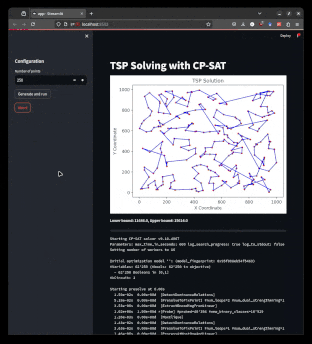 |
|---|
| Using multiprocessing, one can build a responsive interface for a solver. |
@oulianov deployed it here for you to try out in your browser.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.