The CP-SAT Primer: Using and Understanding Google OR-Tools’ CP-SAT Solver

By Dominik Krupke, TU Braunschweig, with contributions from Leon Lan, Michael Perk, and others.
Many combinatorially difficult optimization problems can, despite their proven theoretical hardness, be solved reasonably well in practice. The most successful approach is to use Mixed Integer Linear Programming (MIP) to model the problem and then use a solver to find a solution. The most successful solvers for MIPs are, e.g., Gurobi, CPLEX, COPT Cardinal Solver, and FICO Xpress Optimization, which are all commercial and expensive (though, mostly free for academics). There are also some open source solvers (e.g., SCIP and HiGHS), but they are often not as powerful as the commercial ones (yet). However, even when investing in such a solver, the underlying techniques (Branch and Bound & Cut on Linear Relaxations) struggle with some optimization problems, especially if the problem contains a lot of logical constraints that a solution has to satisfy. In this case, the Constraint Programming (CP) approach may be more successful. For Constraint Programming, there are many open source solvers, but they usually do not scale as well as MIP-solvers and are worse in optimizing objective functions. While MIP-solvers are frequently able to optimize problems with hundreds of thousands of variables and constraints, the classical CP-solvers often struggle with problems with more than a few thousand variables and constraints. However, the relatively new CP-SAT of Google’s OR-Tools suite shows to overcome many of the weaknesses and provides a viable alternative to MIP-solvers, being competitive for many problems and sometimes even superior.
As a quick demonstration of CP-SAT’s capabilities - particularly for those less familiar with optimization frameworks - let us solve an instance of the NP-hard Knapsack Problem. This classic optimization problem requires selecting a subset of items, each with a specific weight and value, to maximize the total value without exceeding a weight limit. Although a recursive algorithm is easy to implement, 100 items yield approximately \( 2^{100} \approx 10^{30} \) possible solutions. Even with a supercomputer performing \( 10^{18} \) operations per second, it would take more than 31,000 years to evaluate all possibilities.
Here is how you can solve it using CP-SAT:
from ortools.sat.python import cp_model # pip install -U ortools
# Specifying the input
weights = [395, 658, 113, 185, 336, 494, 294, 295, 256, 530, 311, 321, 602, 855, 209, 647, 520, 387, 743, 26, 54, 420, 667, 971, 171, 354, 962, 454, 589, 131, 342, 449, 648, 14, 201, 150, 602, 831, 941, 747, 444, 982, 732, 350, 683, 279, 667, 400, 441, 786, 309, 887, 189, 119, 209, 532, 461, 420, 14, 788, 691, 510, 961, 528, 538, 476, 49, 404, 761, 435, 729, 245, 204, 401, 347, 674, 75, 40, 882, 520, 692, 104, 512, 97, 713, 779, 224, 357, 193, 431, 442, 816, 920, 28, 143, 388, 23, 374, 905, 942]
values = [71, 15, 100, 37, 77, 28, 71, 30, 40, 22, 28, 39, 43, 61, 57, 100, 28, 47, 32, 66, 79, 70, 86, 86, 22, 57, 29, 38, 83, 73, 91, 54, 61, 63, 45, 30, 51, 5, 83, 18, 72, 89, 27, 66, 43, 64, 22, 23, 22, 72, 10, 29, 59, 45, 65, 38, 22, 68, 23, 13, 45, 34, 63, 34, 38, 30, 82, 33, 64, 100, 26, 50, 66, 40, 85, 71, 54, 25, 100, 74, 96, 62, 58, 21, 35, 36, 91, 7, 19, 32, 77, 70, 23, 43, 78, 98, 30, 12, 76, 38]
capacity = 2000
# Now we solve the problem
model = cp_model.CpModel()
xs = [model.new_bool_var(f"x_{i}") for i in range(len(weights))]
accumulated_weight = sum(x * w for x, w in zip(xs, weights))
model.add(accumulated_weight <= capacity)
accumulated_value = sum(x * v for x, v in zip(xs, values))
model.maximize(accumulated_value)
solver = cp_model.CpSolver()
solver.solve(model)
print("Optimal selection:", [i for i, x in enumerate(xs) if solver.value(x)])
print("Total packed value:", solver.objective_value)
Optimal selection: [2, 14, 19, 20, 29, 33, 52, 53, 54, 58, 66, 72, 76, 77, 81, 86, 93, 94, 96]
Total packed value: 1161.0
How long did CP-SAT take? On my machine, it found the provably best solution from \( 2^{100} \) possibilities in just 0.01 seconds. Feel free to try it on yours. CP-SAT does not evaluate all solutions; it uses advanced techniques to make deductions and prune the search space. While more efficient approaches than a naive recursive algorithm exist, matching CP-SAT’s performance would require significant time and effort. And this is just the beginning - CP-SAT can tackle much more complex problems, as we will see in this primer.
|
Not convinced yet of why tools like CP-SAT are amazing? Maybe Marco Lübbecke can convince you in his 12-minute TEDx talk Anything you can do I can do better about mathematical optimization.  |
Content
Whether you are from the MIP community seeking alternatives or CP-SAT is your first optimization solver, this book will guide you through the fundamentals of CP-SAT in the first part, demonstrating all its features. The second part will equip you with the skills needed to build and deploy optimization algorithms using CP-SAT.
The first part introduces the fundamentals of CP-SAT, starting with a chapter on installation. This chapter guides you through setting up CP-SAT and outlines the necessary hardware requirements. The next chapter provides a simple example of using CP-SAT, explaining the mathematical notation and its approximation in Python with overloaded operators. You will then progress to basic modeling, learning how to create variables, objectives, and fundamental constraints in CP-SAT.
Following this, a chapter on advanced modeling will teach you how to handle complex constraints, such as circuit constraints and intervals, with practical examples. Another chapter discusses specifying CP-SAT’s behavior, including setting time limits and using parallelization. You will also find a chapter on interpreting CP-SAT logs, which helps you understand how well CP-SAT is managing your problem. Additionally, there is an overview of the underlying techniques used in CP-SAT. The first part concludes with a chapter comparing CP-SAT with other optimization techniques and tools, providing a broader context.
The second part delves into more advanced topics, focusing on general skills like coding patterns and benchmarking rather than specific CP-SAT features. A chapter on coding patterns offers basic design patterns for creating maintainable algorithms with CP-SAT. Another chapter explains how to provide your optimization algorithm as a service by building an optimization API. There is also a chapter on developing powerful heuristics using CP-SAT for particularly difficult or large problems. The second part concludes with a chapter on benchmarking, offering guidance on how to scientifically benchmark your model and interpret the results.
Target Audience
I wrote this book for my computer science students at TU Braunschweig, and it is used as supplementary material in my algorithm engineering courses. Initially, we focused on Mixed Integer Programming (MIP), with CP-SAT discussed as an alternative. However, we recently began using CP-SAT as the first optimization solver due to its high-level interface, which is much easier for beginners to grasp. Despite this shift, because MIP is more commonly used, the book includes numerous comparisons to MIP. Thus, it is designed to be beginner-friendly while also addressing the needs of MIP users seeking alternatives.
Unlike other books aimed at mathematical optimization or operations research students, this one, aimed at computer science students, emphasizes coding over mathematics or business cases, providing a hands-on approach to learning optimization. The second part of the book can also be interesting for more advanced users, providing content that I found missing in other books on optimization.
Table of Content
Part 1: The Basics
- Installation: Quick installation guide.
- Example: A short example, showing the usage of CP-SAT.
- Basic Modeling: An overview of variables, objectives, and constraints.
- Advanced Modeling: More complex constraints, such as circuit constraints and intervals.
- Parameters: How to specify CP-SATs behavior, if needed. Timelimits, hints, assumptions, parallelization, …
- Understanding the Log: How to interpret the log
- How does it work?: After we know what we can do with CP-SAT, we look into how CP-SAT will do all these things.
- Alternatives: An overview of the different optimization techniques and tools available. Putting CP-SAT into context.
- MathOpt as a Modeling Layer: A new modeling layer in OR-Tools that allows using CP-SAT as a backend solver, but also MIP solvers such as Gurobi or HiGHS.
Part 2: Advanced Topics
- Coding Patterns: Basic design patterns for creating maintainable algorithms.
- (Draft) Test-Driven Development: How to develop your optimization algorithm using test-driven development.
- Building an Optimization API How to build a scalable API for long running optimization jobs.
- CP-SAT vs. ML vs. QC: A comparison of CP-SAT with Machine Learning and Quantum Computing.
- Large Neighborhood Search: The use of CP-SAT to create more powerful heuristics.
- Benchmarking your Model: How to benchmark your model and how to interpret the results.
Background
This book assumes you are fluent in Python, and have already been introduced to combinatorial optimization problems. In case you are just getting into combinatorial optimization and are learning on your own, I recommend starting with In Pursuit of the Traveling Salesman by Bill Cook. This book, along with this YouTube talk by the author that lasts about an hour, offers an engaging case study of the well-known Traveling Salesman Problem. It not only introduces fundamental techniques but also delves into the community and historical context of the field.
Additionally, the article Mathematical Programming by CP-SAT’s competitor Gurobi offers an insightful introduction to mathematical programming and modeling. In this context, the term “Programming” does not refer to coding; rather, it originates from an earlier usage of the word “program”, which denoted a plan of action or a schedule. If this distinction is new to you, it is a strong indication that you would benefit from reading this article.
About the Lead Author: Dr. Dominik Krupke is a postdoctoral researcher with the Algorithms Division at TU Braunschweig. He specializes in practical solutions to NP-hard problems. Initially focused on theoretical computer science, he now applies his expertise to solve what was once deemed impossible, frequently with the help of CP-SAT. This primer on CP-SAT, first developed as course material for his students, has been extended in his spare time to cater to a wider audience.
Contributors: This primer has been enriched by the contributions of several individuals. Notably, Leon Lan played a key role in restructuring the content and offering critical feedback, while Michael Perk significantly enhanced the section on the reservoir constraint. I also extend my gratitude to all other contributors who identified and corrected errors, improved the text, and offered valuable insights.
Found a mistake? Please open an issue or a pull request. You can also just write me a quick mail to
krupked@gmail.com.
Want to contribute? If you are interested in contributing, please open an issue or email me with a brief description of your proposal. We can then discuss the details. I welcome all assistance and am open to expanding the content. Contributors to any section or similar input will be recognized as coauthors.
Want to use/share this content? This tutorial can be freely used under CC-BY 4.0. Smaller parts can even be copied without any acknowledgement for non-commercial, educational purposes.
Why are there so many platypuses in the text? I enjoy incorporating elements in my texts that add a light-hearted touch. The choice of the platypus is intentional: much like CP-SAT integrates diverse elements from various domains, the platypus combines traits from different animals. The platypus also symbolizes Australia, home to the development of a key technique in CP-SAT - Lazy Clause Generation (LCG).
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Part 1: The Basics
Installation
We are using Python 3 in this primer and assume that you have a working Python 3 installation as well as the basic knowledge to use it. There are also interfaces for other languages, but Python 3 is, in my opinion, the most convenient one, as the mathematical expressions in Python are very close to the mathematical notation (allowing you to spot mathematical errors much faster). Only for huge models, you may need to use a compiled language such as C++ due to performance issues. For smaller models, you will not notice any performance difference.
The installation of CP-SAT, which is part of the OR-Tools package, is very easy and can be done via Python’s package manager pip.
pip3 install -U ortools
This command will also update an existing installation of OR-Tools. As this tool is in active development, it is recommended to update it frequently. We actually encountered wrong behavior, i.e., bugs, in earlier versions that then have been fixed by updates (this was on some more advanced features, do not worry about correctness with basic usage).
I personally like to use Jupyter Notebooks for experimenting with CP-SAT.
What hardware do you need?
It is important to note that for CP-SAT usage, you do not need the capabilities of a supercomputer. A standard laptop is often sufficient for solving many problems. The primary requirements are CPU power and memory bandwidth, with a GPU being unnecessary.
In terms of CPU power, the key is balancing the number of cores with the performance of each individual core. CP-SAT leverages all available cores by default, implementing different strategies on each. Depending on the number of cores, CP-SAT will behave differently. However, the effectiveness of these strategies can vary, and it is usually not apparent which one will be most effective. A higher single-core performance means that your primary strategy will operate more swiftly. I recommend a minimum of 4 cores and 16GB of RAM.
While CP-SAT is quite efficient in terms of memory usage, the amount of available memory can still be a limiting factor in the size of problems you can tackle. When it came to setting up our lab for extensive benchmarking at TU Braunschweig, we faced a choice between desktop machines and more expensive workstations or servers. We chose desktop machines equipped with AMD Ryzen 9 7900 CPUs (Intel would be equally suitable) and 96GB of DDR5 RAM, managed using Slurm. This decision was driven by the fact that the performance gains from higher-priced workstations or servers were relatively marginal compared to their significantly higher costs. When on the road, I am often still able to do stuff with my old Intel Macbook Pro from 2018 with an i7 and only 16GB of RAM, but large models will overwhelm it. My workstation at home with AMD Ryzen 7 5700X and 32GB of RAM on the other hand rarely has any problems with the models I am working on.
For further guidance, consider the hardware recommendations for the Gurobi solver, which are likely to be similar. Since we frequently use Gurobi in addition to CP-SAT, our hardware choices were also influenced by their recommendations.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Example
A Simple Example

Before we dive into any internals, let us take a quick look at a simple application of CP-SAT. This example is so simple that you could solve it by hand, but know that CP-SAT would (probably) be fine with you adding a thousand (maybe even ten- or hundred-thousand) variables and constraints more. The basic idea of using CP-SAT is, analogous to MIPs, to define an optimization problem in terms of variables, constraints, and objective function, and then let the solver find a solution for it. We call such a formulation that can be understood by the corresponding solver a model for the problem. For people not familiar with this declarative approach, you can compare it to SQL, where you also just state what data you want, not how to get it. However, it is not purely declarative, because it can still make a huge(!) difference how you model the problem and getting that right takes some experience and understanding of the internals. You can still get lucky for smaller problems (let us say a few hundred to thousands of variables) and obtain optimal solutions without having an idea of what is going on. The solvers can handle more and more ‘bad’ problem models effectively with every year.
 A model in mathematical programming refers to a mathematical description of a problem, consisting of variables, constraints, and optionally an objective function that can be understood by the corresponding solver class. Modelling refers to transforming a problem (instance) into the corresponding framework, e.g., by making all constraints linear as required for Mixed Integer Linear Programming. Be aware that the SAT-community uses the term model to refer to a (feasible) variable assignment, i.e., solution of a SAT-formula. If you struggle with this terminology, maybe you want to read this short guide on Math Programming Modelling Basics. |
Our first problem has no deeper meaning, except for showing the basic workflow of creating the variables (x and y), adding the constraint \( x+y<=30 \) on them, setting the objective function (maximize \( 30x + 50y \)), and obtaining a solution:
from ortools.sat.python import cp_model
model = cp_model.CpModel()
# Variables
x = model.new_int_var(0, 100, "x")
y = model.new_int_var(0, 100, "y")
# Constraints
model.add(x + y <= 30)
# Objective
model.maximize(30 * x + 50 * y)
# Solve
solver = cp_model.CpSolver()
status_code = solver.solve(model)
status_name = solver.status_name()
# Print the solver status and the optimal solution.
print(f"{status_name} ({status_code})")
print(f"x={solver.value(x)}, y={solver.value(y)}")
OPTIMAL (4)
x=0, y=30
Pretty easy, right? For solving a generic problem, not just one specific
instance, you would of course create a dictionary or list of variables and use
something like model.add(sum(vars)<=n), because you do not want to create the
model by hand for larger instances.
The solver can return five different statuses:
| Status | Code | Description |
|---|---|---|
UNKNOWN | 0 | The solver has not run for long enough. |
MODEL_INVALID | 1 | The model is invalid. You will rarely see that status. |
FEASIBLE | 2 | The model has a feasible, but not necessarily optimal, solution. If your model does not have an objective, every feasible model will return OPTIMAL, which may be counterintuitive. |
INFEASIBLE | 3 | The model has no feasible solution. This means that your constraints are too restrictive. |
OPTIMAL | 4 | The model has an optimal solution. If your model does not have an objective, OPTIMAL is returned instead of FEASIBLE. |
 The status |
For larger models, CP-SAT will unfortunately not always able to compute an optimal solution. However, the good news is that the solver will likely still find a satisfactory solution and provide a bound on the optimal solution. Once you reach this point, understanding how to interpret the solver’s log becomes crucial for analyzing the solver’s performance. We will learn more about this later.
Mathematical Model
The mathematical model of the code above would usually be written by experts something like this:
\[ \max 30x + 50y \]
\[ \text{s.t. } x+y \leq 30 \]
\[ \quad 0\leq x \leq 100 \]
\[ \quad 0\leq y \leq 100 \]
\[ x,y \in \mathbb{Z} \]
The s.t. stands for subject to, sometimes also read as such that.
Overloading
One aspect of using CP-SAT solver that often poses challenges for learners is
understanding operator overloading in Python and the distinction between the two
types of variables involved. In this context, x and y serve as mathematical
variables. That is, they are placeholders that will only be assigned specific
values during the solving phase. To illustrate this more clearly, let us explore
an example within the Python shell:
>>> model = cp_model.CpModel()
>>> x = model.new_int_var(0, 100, "x")
>>> x
x(0..100)
>>> type(x)
<class 'ortools.sat.python.cp_model.IntVar'>
>>> x + 1
sum(x(0..100), 1)
>>> x + 1 <= 1
<ortools.sat.python.cp_model.BoundedLinearExpression object at 0x7d8d5a765df0>
In this example, x is not a conventional number but a placeholder defined to
potentially assume any value between 0 and 100. When 1 is added to x, the
result is a new placeholder representing the sum of x and 1. Similarly,
comparing this sum to 1 produces another placeholder, which encapsulates the
comparison of the sum with 1. These placeholders do not hold concrete values at
this stage but are essential for defining constraints within the model.
Attempting operations like if x + 1 <= 1: print("True") will trigger a
NotImplementedError, as the condition x+1<=1 cannot be evaluated directly.
Although this approach to defining models might initially seem perplexing, it facilitates a closer alignment with mathematical notation, which in turn can make it easier to identify and correct errors in the modeling process.
More examples
If you are not yet satisfied, this folder contains many Jupyter Notebooks with examples from the developers. For example
- multiple_knapsack_sat.ipynb shows how to solve a multiple knapsack problem.
- nurses_sat.ipynb shows how to schedule the shifts of nurses.
- bin_packing_sat.ipynb shows how to solve a bin packing problem.
- … (if you know more good examples I should mention here, please let me know!)
Further, you can find an extensive and beginner-friendly example on scheduling workers here.
Now that you have seen a minimal model, let us explore the various options available for problem modeling. While an experienced optimizer might be able to handle most problems using just the elements previously discussed, clearly expressing your intentions can help CP-SAT optimize your problem more effectively.
|
Optimization problems are everywhere in the real world. If you want a quick overview of practical applications, the video Optimization 360 (Optimization Everywhere) from Gurobi’s Opti 202 Training highlights a variety of domains where optimization plays a key role. Here is a summary table of example problems from the video:
 |
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Basic Modeling
Basic Modeling

In this chapter, we dive into the basic modeling capabilities of CP-SAT. CP-SAT
provides an extensive set of constraints, closer to high-level modeling
languages like MiniZinc than to traditional Mixed Integer Programming (MIP). For
example, it offers constraints like all_different and
add_multiplication_equality. These advanced features reduce the need for
modeling complex logic strictly through linear constraints, though they also
increase the interface’s complexity. However, not all constraints are equally
efficient; linear and boolean constraints are generally most efficient, whereas
constraints like add_multiplication_equality can be significantly more
resource-intensive.
 If you are transitioning from Mixed Integer Programming (MIP), you might be used to manually implementing higher-level constraints and optimizing Big-M parameters for better performance. With CP-SAT, such manual adjustments are generally unnecessary. CP-SAT operates differently from typical MIP solvers by relying less on linear relaxation and more on its underlying SAT-solver and propagators to efficiently manage logical constraints. Embrace the higher-level constraints—they are often more efficient in CP-SAT. |
This primer has been expanded to cover all constraints across two chapters, complete with various examples to illustrate the contexts in which they can be used. However, mastering modeling involves much more than just an understanding of constraints. It requires a deep appreciation of the principles and techniques that make models effective and applicable to real-world problems.
For a more detailed exploration of modeling, consider “Model Building in Mathematical Programming” by H. Paul Williams, which offers extensive insight into the subject, including practical applications. While this book is not specific to CP-SAT, the foundational techniques and concepts are broadly applicable. Additionally, for those new to this area or transitioning from MIP solutions, studying Gurobi’s modeling approach through this video course might prove helpful. While many principles overlap, some strategies unique to CP-SAT can better address cases where traditional MIP-solvers struggle.
Additional resources on mathematical modeling (not CP-SAT specific):
- Math Programming Modeling Basics by Gurobi: This resource provides a solid introduction to the basics of mathematical modeling.
- Modeling with Gurobi Python: A comprehensive video course on modeling with Gurobi, highlighting concepts that are also applicable to CP-SAT.
- Model Building in Mathematical Programming by H. Paul Williams: An extensive guide to mathematical modeling techniques.
 For getting started with implementing optimization models in general, I highly recommend the blog post The Art Of Not Making It An Art. It excellently summarizes the fundamental principles of successfully managing an optimization project, independent of the concrete language or solver. |
Elements:
- Variables:
new_int_var,new_bool_var,new_constant,new_int_var_series,new_bool_var_series- Custom Domain Variables:
new_int_var_from_domain
- Custom Domain Variables:
- Objectives:
minimize,maximize - Linear Constraints:
add,add_linear_constraint - Logical Constraints (Propositional Logic):
add_implication,add_bool_or,add_at_least_one,add_at_most_one,add_exactly_one,add_bool_and,add_bool_xor - Conditional Constraints (Reification):
only_enforce_if - Absolute Values and Max/Min:
add_min_equality,add_max_equality,add_abs_equality - Multiplication, Division, and Modulo:
add_modulo_equality,add_multiplication_equality,add_division_equality - All Different:
add_all_different - Domains and Combinations:
add_allowed_assignments,add_forbidden_assignments - Array/Element Constraints:
add_element,add_inverse
The more advanced constraints add_circuit, add_multiple_circuit,
add_automaton,add_reservoir_constraint,
add_reservoir_constraint_with_active, new_interval_var,
new_interval_var_series, new_fixed_size_interval_var,
new_optional_interval_var, new_optional_interval_var_series,
new_optional_fixed_size_interval_var,
new_optional_fixed_size_interval_var_series, add_no_overlap,
add_no_overlap_2d, and add_cumulative are discussed in the next chapter.
Variables
There are two important types of variables in CP-SAT: Booleans and Integers (which are actually converted to Booleans, but more on this later). There are also, e.g., interval variables, but they are actually rather a combination of integral variables and discussed later. For the integer variables, you have to specify a lower and an upper bound.
model = cp_model.CpModel()
# Integer variable z with bounds -100 <= z <= 100
z = model.new_int_var(-100, 100, "z") # new syntax
z_ = model.NewIntVar(-100, 100, "z_") # old syntax
# Boolean variable b
b = model.new_bool_var("b") # new syntax
b_ = model.NewBoolVar("b_") # old syntax
# Implicitly available negation of b:
not_b = ~b # will be 1 if b is 0 and 0 if b is 1
not_b_ = b.Not() # old syntax
Additionally, you can use model.new_int_var_series and
model.new_bool_var_series to create multiple variables at once from a pandas
Index. This is especially useful if your data is given in a pandas DataFrame.
However, there is no performance benefit in using this method, it is just more
convenient.
model = cp_model.CpModel()
# Create an Index from 0 to 9
index = pd.Index(range(10), name="index")
# Create a pandas Series with 10 integer variables matching the index
xs = model.new_int_var_series("x", index, 0, 100)
# List of boolean variables
df = pd.DataFrame(
data={"weight": [1 for _ in range(10)], "value": [3 for _ in range(10)]},
index=["A", "B", "C", "D", "E", "F", "G", "H", "I", "J"],
)
bs = model.new_bool_var_series("b", df.index) # noqa: F841
# Using the dot product on the pandas DataFrame is actually a pretty
# convenient way to create common linear expressions.
model.add(bs @ df["weight"] <= 100)
model.maximize(bs @ df["value"])
Additionally, there is the new_constant-method, which allows you to create a
variable that is constant. This allows you to safely replace variables by
constants. This is primarily useful for boolean variables, as constant integer
variables can in most cases be simply replaced by plain integers.
 In an older project, I observed that maintaining tight bounds on integer variables can significantly impact performance. Employing a heuristic to find a reasonable initial solution, which then allowed for tighter bounds, proved worthwhile, even though the bounds were just a few percent tighter. Although this project was several years ago and CP-SAT has advanced considerably since then, I still recommend keeping the bounds on the variables’ ranges as tight as possible. |
There are no continuous/floating point variables (or even constants) in CP-SAT: If you need floating point numbers, you have to approximate them with integers by some resolution. For example, you could simply multiply all values by 100 for a step size of 0.01. A value of 2.35 would then be represented by 235. This could probably be implemented in CP-SAT directly, but doing it explicitly is not difficult, and it has numerical implications that you should be aware of.
The absence of continuous variables may appear as a substantial limitation, especially for those with a background in linear optimization where continuous variables are typically regarded as the simpler component. However, if your problem includes only a few continuous variables that must be approximated using large integers and involves complex constraints such as absolute values, while the majority of the problem is dominated by logical constraints, CP-SAT can often outperform mixed-integer programming solvers. It is only when a problem contains a substantial number of continuous variables and benefits significantly from strong linear relaxation that mixed-integer programming solvers will have a distinct advantage, despite CP-SAT having a propagator based on the dual simplex method.
I analyzed the impact of resolution (i.e., the factor by which floating point numbers are multiplied) on the runtime of CP-SAT, finding that the effect varied depending on the problem. For one problem, the runtime increased only logarithmically with the resolution, allowing the use of a very high resolution of 100,000x without significant issues. In contrast, for another problem, the runtime increased roughly linearly with the resolution, making high resolutions impractical. The runtime for different factors in this case was: 1x: 0.02s, 10x: 0.7s, 100x: 7.6s, 1000x: 75s, and 10,000x: over 15 minutes, even though the solution remained the same, merely scaled. Therefore, while high resolutions may be feasible for some problems using CP-SAT, it is essential to verify their influence on runtime, as the impact can be considerable.
In my experience, boolean variables are crucial in many combinatorial optimization problems. For instance, the famous Traveling Salesman Problem consists solely of boolean variables. Therefore, implementing a solver that specializes in boolean variables using a SAT-solver as a foundation, such as CP-SAT, is a sensible approach. CP-SAT leverages the strengths of SAT-solving techniques, which are highly effective for problems dominated by boolean variables.
You may wonder why it is necessary to explicitly name the variables in CP-SAT. While there does not appear to be a technical reason for this requirement, naming the variables can be extremely helpful for debugging purposes. Understanding the naming scheme of the variables allows you to more easily interpret the internal representation of the model, facilitating the identification and resolution of issues. To be fair, there have only been a few times when I actually needed to take a closer at the internal representation, and in most of the cases I would have preferred not to have to name the variables.
Custom Domain Variables
When dealing with integer variables that you know will only need to take certain values, or when you wish to limit their possible values, custom domain variables can become interesting. Unlike regular integer variables, which must have a domain between a given range of values (e.g., \( [ 1, 100 ] \)), domain variables can specify a custom set of values as domain (e.g., \( \{1, 31, 57 \} \)). This can improve efficiency if the variable’s feasible values are substantially reduced. However, it also introduces drawbacks, which we discuss below.
CP-SAT works by converting all integer variables into boolean variables (warning: simplification). For each potential value, it creates two boolean variables: one indicating whether the integer variable is equal to this value, and another indicating whether it is less than or equal to it. This is called an order encoding. At first glance, this might suggest that using domain variables is always preferable, as it appears to reduce the number of boolean variables needed.
However, CP-SAT employs a lazy creation strategy for these boolean variables. This means it only generates them as needed, based on the solver’s decision-making process. Therefore, an integer variable with a wide range - say, from 0 to 100 - will not immediately result in 200 boolean variables. It might lead to the creation of only a few, depending on the solver’s requirements.
Limiting the domain of a variable can have drawbacks. First, if the assumptions about admissible values are incorrect, it may introduce subtle and difficult-to-detect bugs. Therefore, it is advisable to prioritize correctness before attempting such optimizations. Second, specifying an explicit domain can significantly increase the model size, as the solver must handle a list of discrete values rather than a simple lower and upper bound. For example, if a variable is restricted to even values, it would be inefficient to define a domain consisting of all even numbers. In this case, a better approach is to substitute the variable \( x \) with \( 2x’ \), and subsequently multiply \( x’ \) by \( 2 \) in the final solution. Third, in certain instances, the use of custom domains may delay the discovery of an initial solution. Since CP-SAT relies on its powerful neighborhood search to improve solutions after the first feasible one is found, this delay can hinder solver performance. Unless the domain restriction itself encodes a meaningful modeling constraint, it is generally preferable to defer its use until performance optimization becomes necessary.
If you choose to utilize domain variables for their benefits in specific scenarios, here is how to define them:
from ortools.sat.python import cp_model
model = cp_model.CpModel()
# Define a domain with selected values
domain = cp_model.Domain.from_values([2, 5, 8, 10, 20, 50, 90])
# Can also be done via intervals
domain_2 = cp_model.Domain.from_intervals([[8, 12], [14, 20]])
# There are also some operations available
domain_3 = domain.union_with(domain_2)
# Create a domain variable within this defined domain
x = model.new_int_var_from_domain(domain, "x")
This example illustrates the process of creating a domain variable x that can
only take on the values specified in domain. This method is particularly
useful when you are working with variables that only have a meaningful range of
possible values within your problem’s context.
Objectives
Not every problem necessitates an objective; sometimes, finding a feasible solution is sufficient. CP-SAT excels at finding feasible solutions, a task at which mixed-integer programming (MIP) solvers often do not perform as well. However, CP-SAT is also capable of effective optimization, which is an area where older constraint programming solvers may lag, based on my experience.
CP-SAT allows for the minimization or maximization of a linear expression. You
can model more complex expressions by using auxiliary variables and additional
constraints. To specify an objective function, you can use the model.minimize
or model.maximize commands with a linear expression. This flexibility makes
CP-SAT a robust tool for a variety of optimization tasks.
# Basic model with variables and constraints
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
model.add(x + 10 * y <= 100)
# Minimize 30x + 50y
model.maximize(30 * x + 50 * y)
Let us look on how to model more complicated expressions, using boolean variables and generators.
model = cp_model.CpModel()
x_vars = [model.new_bool_var(f"x{i}") for i in range(10)]
model.minimize(sum(i * x_vars[i] if i % 2 == 0 else i * ~x_vars[i] for i in range(10)))
This objective evaluates to
\[ \min \sum_{i=0}^{9} i\cdot x_i \text{ if } i \text{ is even else } i\cdot \neg x_i \]
To implement a lexicographic optimization, you can do multiple rounds and always fix the previous objective as constraint.
# some basic model
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
model.add(x + 10 * y - 2 * z <= 100)
# Define the objectives
first_objective = 30 * x + 50 * y
second_objective = 10 * x + 20 * y + 30 * z
# Optimize for the first objective
model.maximize(first_objective)
solver = cp_model.CpSolver()
solver.solve(model)
# Fix the first objective and optimize for the second
model.add(first_objective == int(solver.objective_value)) # fix previous objective
model.minimize(second_objective) # optimize for second objective
solver.solve(model)
 You can find a more efficient implementation of lexicographic optimization in the Coding Patterns chapter. |
To handle non-linear objectives in CP-SAT, you can employ auxiliary variables
and constraints. For instance, to incorporate the absolute value of a variable
into your objective, you first create a new variable representing this absolute
value. Shortly, you will learn more about setting up these types of constraints.
Below is a Python example demonstrating how to model and minimize the absolute
value of a variable x:
# Assuming x is already defined in your model
abs_x = model.new_int_var(
0, 100, "|x|"
) # Create a variable to represent the absolute value of x
model.add_abs_equality(target=abs_x, expr=x) # Define abs_x as the absolute value of x
model.minimize(abs_x) # Set the objective to minimize abs_x
The constraints available to define your feasible solution space will be discussed in the following section.
Linear Constraints
These are the classical constraints also used in linear optimization. Remember that you are still not allowed to use floating point numbers within it. Same as for linear optimization: You are not allowed to multiply a variable with anything else than a constant and also not to apply any further mathematical operations.
model.add(10 * x + 15 * y <= 10)
model.add(x + z == 2 * y)
# This one actually is not linear but still works.
model.add(x + y != z)
# Because we are working on integers, the true smaller or greater constraints
# are trivial to implement as x < z is equivalent to x <= z-1
model.add(x < y + z)
model.add(y > 300 - 4 * z)
Note that != can be slower than the other (<=, >=, ==) constraints,
because it is not a linear constraint. If you have a set of mutually !=
variables, it is better to use all_different (see below) than to use the
explicit != constraints.
 If you use intersecting linear constraints, you may get problems because the intersection point needs to be integral. There is no such thing as a feasibility tolerance as in Mixed Integer Programming-solvers, where small deviations are allowed. The feasibility tolerance in MIP-solvers allows, e.g., 0.763445 == 0.763439 to still be considered equal to counter numerical issues of floating point arithmetic. In CP-SAT, you have to make sure that values can match exactly. |
Let us look at the following example with two linear equality constraints:
\[ x - y = 0 \]
\[ 4-x = 2y \]
\[ x, y \geq 0 \]
You can verify that \( x=4/3 \) and \( y=4/3 \) is a feasible solution. However, coding this in CP-SAT results in an infeasible solution:
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
model.add(x - y == 0)
model.add(4 - x == 2 * y)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.INFEASIBLE
Even using scaling techniques, such as multiplying integer variables by 1,000,000 to increase the resolution, would not render the model feasible. While common linear programming solvers would handle this model without issue, CP-SAT struggles unless modifications are made to eliminate fractions, such as multiplying all terms by 3. However, this requires manual intervention, which undermines the idea of using a solver. These limitations are important to consider, although such scenarios are rare in practical applications.
 If you have long sums of variables and coefficients, it can be more efficient to use the sum-methods of LinearExpr than to use Python’s sum-function. Note that this function does currently not support generators. |
If you have a lower and an upper bound for a linear expression, you can also use
the add_linear_constraint-method, which allows you to specify both bounds in
one go.
model.add_linear_constraint(linear_expr=10 * x + 15 * y, lb=-100, ub=10)
The similar sounding AddLinearExpressionInDomain is discussed later.
Logical Constraints (Propositional Logic)
Propositional logic allows us to describe relationships between true or false statements using logical operators. Consider a simple scenario where we define three Boolean variables:
b1 = model.new_bool_var("b1")
b2 = model.new_bool_var("b2")
b3 = model.new_bool_var("b3")
These variables, b1, b2, and b3, represent distinct propositions whose
truth values are to be determined by the model.
You can obtain the negation of a Boolean variable by using ~ or the
.Not()-method. The resulting variable can be used just like the original
variable:
not_b1 = ~b1 # Negation of b1
not_b2 = b2.Not() # Alternative notation for negation
Note that you can use more than three variables in all of the following
examples, except for add_implication which is only defined for two variables.
 Boolean variables are essentially special integer variables restricted to the domain of 0 and 1. Therefore, you can incorporate them into linear constraints as well. However, it is important to note that integer variables, unlike Boolean variables, cannot be used in Boolean constraints. This is a distinction from some programming languages, like Python, where integers can sometimes substitute for Booleans. |
Adding Logical OR Constraints
The logical OR operation ensures that at least one of the specified conditions holds true. To model this, you can use:
model.add_bool_or(b1, b2, b3) # b1 or b2 or b3 must be true
model.add_at_least_one([b1, b2, b3]) # Alternative notation
model.add(b1 + b2 + b3 >= 1) # Alternative linear notation using '+' for OR
Both lines ensure that at least one of b1, b2, or b3 is true.
Adding Logical AND Constraints
The logical AND operation specifies that all conditions must be true
simultaneously. To model conditions where b1 is true and both b2 and b3
are false, you can use:
model.add_bool_and(b1, b2.Not(), b3.Not()) # b1 and not b2 and not b3 must all be true
model.add_bool_and(b1, ~b2, ~b3) # Alternative notation using '~' for negation
The add_bool_and method is most effective when used with the only_enforce_if
method (discussed in
Conditional Constraints (Reification)).
For cases not utilizing only_enforce_if a simple AND-clause such as
\( \left( b_1 \land \neg b_2 \land \neg b_3 \right) \) becomes redundant by simply
substituting \( b_1 \) with 1 and \( b_2, b_3 \) with 0. In straightforward
scenarios, consider substituting these variables with their constant values to
reduce unnecessary complexity, especially in larger models where size and
manageability are concerns. In smaller or simpler models, CP-SAT efficiently
handles these redundancies, allowing you to focus on maintaining clarity and
readability in your model.
Adding Logical XOR Constraints
The logical XOR (exclusive OR) operation ensures that an odd number of operands are true. It is crucial to understand this definition, as it has specific implications when applied to more than two variables:
- For two variables, such as
b1 XOR b2, the operation returns true if exactly one of these variables is true, which aligns with the “exactly one” constraint for this specific case. - For three or more variables, such as in the expression
b1 XOR b2 XOR b3, the operation returns true if an odd number of these variables are true. This includes scenarios where one or three variables are true, assuming the total number of variables involved is three.
This characteristic of XOR can be somewhat complex but is crucial for modeling scenarios where the number of true conditions needs to be odd:
model.add_bool_xor(b1, b2) # Returns true if exactly one of b1 or b2 is true
model.add_bool_xor(
b1, b2, b3
) # Returns true if an odd number of b1, b2, b3 are true (i.e., one or three)
Specifying Unique Conditions
To enforce that exactly one or at most one of the variables is true, use:
model.add_exactly_one([b1, b2, b3]) # Exactly one of the variables must be true
model.add_at_most_one([b1, b2, b3]) # No more than one of the variables should be true
These constraints are useful for scenarios where exclusive choices must be modeled.
You could alternatively also use add.
model.add(b1 + b2 + b3 == 1) # Exactly one of the variables must be true
model.add(b1 + b2 + b3 <= 1) # No more than one of the variables should be true
Modeling Implications
Logical implication, denoted as ->, indicates that if the first condition is
true, the second must also be true. This can be modeled as:
model.add_implication(b1, b2) # If b1 is true, then b2 must also be true
You could also use add.
model.add(b2 >= b1) # If b1 is true, then b2 must also be true
Equivalent Reformulations of Logical Expressions
Logical expressions are often written in a nested form, but CP-SAT requires a
flat structure. Fortunately, any propositional logic expression can be
reformulated into a flat structure that only uses and_bool_or (also known as
the conjunctive normal form CNF). All other constraints are merely syntactic
sugar, provided to have a more natural modelling experience. While it would be
straightforward for CP-SAT to support nested expressions directly, its
development focuses on its engine rather than the interface. Therefore, at
present, you must perform these reformulations manually (or use
CPMpy).
The most useful reformulations include:
- Implication:
A -> Bis equivalent toNOT A OR B NOT (A AND B)is equivalent toNOT A OR NOT B(De Morgan’s Law 1)NOT (A OR B)is equivalent toNOT A AND NOT B(De Morgan’s Law 2)
These equivalences can be verified using a truth table. Since there are only
four possible combinations of truth values for A and B, you need only check
that the two columns produce identical results:
| A | B | A -> B | NOT A OR B |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Note that A and B may themselves be logical expressions, not just single
variables. A more extensive list of equivalences can be found on
Wikipedia.
|
Logic is a common undergraduate lecture and there are some recorded courses available online in case you would like to refresh your knowledge:
 |
 I can also highly recommend the following chapter of the open-source book Mathematics for Computer Science by Lehman, Leighton, and Meyer. It should not take long to read and lists all the important equivalences. |
Let us consider some examples:
- To model
b1 -> b2, you can usemodel.add_implication(b1, b2). Alternatively, reformulate it asNOT b1 OR b2and usemodel.add_bool_or(~b1, b2). - To model
NOT (b1 AND b2), reformulate it asNOT b1 OR NOT b2and usemodel.add_bool_or(~b1, ~b2). - To model
NOT (b1 OR b2), reformulate it asNOT b1 AND NOT b2and usemodel.add_bool_and(~b1, ~b2). (Even more efficiently, you could directly substituteb1andb2with0, since they can never be true.) - To model
(b1 AND b2) -> b3, reformulate it asNOT (b1 AND b2) OR b3, which is equivalent to(NOT b1 OR NOT b2) OR b3. You can then usemodel.add_bool_or(~b1, ~b2, b3). - To model
(b1 OR b2) -> b3, reformulate it as(b1 -> b3) AND (b2 -> b3), which is equivalent to(NOT b1 OR b3) AND (NOT b2 OR b3). You can then use:model.add_bool_or(~b1, b3) model.add_bool_or(~b2, b3) - To model
b1 -> (b2 OR b3), reformulate it asNOT b1 OR (b2 OR b3), which is equivalent toNOT b1 OR b2 OR b3. You can then usemodel.add_bool_or(~b1, b2, b3). - Expressions of the form
(b1 AND b2) OR (b3 AND b4)can be reformulated using distributive laws to(b1 OR b3) AND (b1 OR b4) AND (b2 OR b3) AND (b2 OR b4). However, for longer expressions, this can lead to an exponential increase in the number of clauses. In such cases, it is often more efficient to introduce auxiliary variables in the form of the Tseytin transformation.
 Awareness of these equivalences can support the modelling of complex logical
expressions and, in some cases, improve performance by replacing expensive
constructs with simpler ones (short |
Conditional Constraints (Reification)
In practical applications, scenarios often arise where conditions dictate the enforcement of certain constraints. For instance, “if this condition is true, then a specific constraint should apply,” or “if a constraint is violated, a penalty variable is set to true, triggering another constraint.” Additionally, real-world constraints can sometimes be bypassed with financial or other types of concessions, such as renting a more expensive truck to exceed a load limit, or allowing a worker to take a day off after a double shift.
In constraint programming, reification involves associating a Boolean variable with a constraint to capture its truth value, thereby turning the satisfaction of the constraint into a variable that can be used in further constraints. Full reification links a Boolean variable such that it is
Trueif the constraint is satisfied andFalseotherwise, enabling the variable to be directly used in other decisions or constraints. Conversely, half-reification, or implied constraints, involves a one-way linkage where the Boolean variable beingTrueimplies the constraint must be satisfied, but its beingFalsedoes not necessarily indicate anything about the constraint’s satisfaction. This approach is particularly useful for expressing complex conditional logic and for modeling scenarios where only the satisfaction, and not the violation, of a constraint needs to be explicitly handled.
To effectively manage these conditional scenarios, CP-SAT offers the
only_enforce_if-method for linear and some Boolean constraints, which
activates a constraint only if a specified condition is met. This method is not
only typically more efficient than traditional methods like the
Big-M method but also simplifies
the model by eliminating the need to determine an appropriate Big-M value.
# A value representing the load that needs to be transported
load_value = model.new_int_var(0, 100, "load_value")
# ... some logic to determine the load value ...
# A variable to decide which truck to rent
truck_a = model.new_bool_var("truck_a")
truck_b = model.new_bool_var("truck_b")
truck_c = model.new_bool_var("truck_c")
# Only rent one truck
model.add_at_most_one([truck_a, truck_b, truck_c])
# Depending on which truck is rented, the load value is limited
model.add(load_value <= 50).only_enforce_if(truck_a)
model.add(load_value <= 80).only_enforce_if(truck_b)
model.add(load_value <= 100).only_enforce_if(truck_c)
# Some additional logic
driver_has_big_truck_license = model.new_bool_var("driver_has_big_truck_license")
driver_has_special_license = model.new_bool_var("driver_has_special_license")
# Only drivers with a big truck license or a special license can rent truck c
model.add_bool_or(
driver_has_big_truck_license, driver_has_special_license
).only_enforce_if(truck_c)
# Minimize the rent cost
model.minimize(30 * truck_a + 40 * truck_b + 80 * truck_c)
You can also use negations in the only_enforce_if method.
model.add(x + y == 10).only_enforce_if(~b1)
You can also pass a list of Boolean variables to only_enforce_if, in which
case the constraint is only enforced if all of the variables in the list are
true.
model.add(x + y == 10).only_enforce_if([b1, ~b2]) # only enforce if b1 AND NOT b2
 While |
Absolute Values and Maximum/Minimum Functions with Integer Variables
When working with integer variables in CP-SAT, operations such as computing
absolute values, maximum, and minimum values cannot be directly expressed using
basic Python operations like abs, max, or min. Instead, these operations
must be handled through the use of auxiliary variables and specialized
constraints that map these variables to the desired values. The auxiliary
variables can then be used in other constraints, representing the desired
subexpression.
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
# Create an auxiliary variable for the absolute value of x+z
abs_xz = model.new_int_var(0, 200, "|x+z|")
model.add_abs_equality(target=abs_xz, expr=x + z)
# Create variables to capture the maximum and minimum of x, (y-1), and z
max_xyz = model.new_int_var(0, 100, "max(x, y-1, z)")
# Changed in ortools 9.15: was add_max_equality(target=max_xyz, exprs=[x, y - 1, z])
model.add_max_equality(max_xyz, x, y - 1, z)
min_xyz = model.new_int_var(-100, 100, "min(x, y-1, z)")
# Changed in ortools 9.15: was add_min_equality(target=min_xyz, exprs=[x, y - 1, z])
model.add_min_equality(min_xyz, x, y - 1, z)
While some practitioners report that these methods are more efficient than those available in classical Mixed Integer Programming solvers, such findings are predominantly based on empirical evidence and specific use-case scenarios. It is also worth noting that, surprisingly often, these constraints can be substituted with more efficient linear constraints. Here is an example for achieving maximum equality in a more efficient way:
x = model.new_int_var(0, 100, "x")
y = model.new_int_var(0, 100, "y")
z = model.new_int_var(0, 100, "z")
# Ensure that max_xyz is at least the maximum of x, y, and z
max_xyz = model.new_int_var(0, 100, "max_xyz")
model.add(max_xyz >= x)
model.add(max_xyz >= y)
model.add(max_xyz >= z)
# Minimizing max_xyz to ensure it accurately reflects the maximum value
model.minimize(max_xyz)
This approach takes advantage of the solver’s minimization function to tighten
the bound, accurately reflecting the maximum of x, y, and z. By utilizing
linear constraints, this method can often achieve faster solving times compared
to using the add_max_equality constraint. Similar techniques also exist for
managing absolute and minimum values, as well as for complex scenarios where
direct enforcement of equality through the objective function is not feasible.
Multiplication, Division, and Modulo
In practical problems, you may need to perform more complex arithmetic
operations than simple additions. Consider the scenario where the rental cost
for a set of trucks is calculated as the product of the number of trucks, the
number of days, and the daily rental rate. Here, the first two factors are
variables, leading to a quadratic expression. Attempting to multiply two
variables directly in CP-SAT will result in an error because the add method
only accepts linear expressions, which are sums of variables and constants.
However, CP-SAT supports multiplication, division, and modulo operations.
Similar to using abs, max, and min, you must create an auxiliary variable
to represent the result of the operation.
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
xyz = model.new_int_var(-(100**3), 100**3, "x*y*z")
model.add_multiplication_equality(xyz, [x, y, z]) # xyz = x*y*z
model.add_modulo_equality(x, y, 3) # x = y % 3
model.add_division_equality(x, y, z) # x = y // z
When using these operations, you often transition from linear to non-linear
optimization, which is generally more challenging to solve. In cases of
division, it is essential to remember that operations are on integers;
therefore, 5 // 2 results in 2, not 2.5.
Many problems initially involve non-linear expressions that can often be reformulated or approximated using linear expressions. This transformation can enhance the tractability and speed of solving the problem. Although modeling your problem as closely as possible to the real-world scenario is crucial, it is equally important to balance accuracy with tractability. A highly accurate model is futile if the solver cannot optimize it efficiently. It might be beneficial to employ multiple phases in your optimization process, starting with a simpler, less accurate model and gradually refining it.
Some non-linear expressions can still be managed efficiently if they are convex. For instance, second-order cone constraints can be solved in polynomial time using interior point methods. Gurobi, for example, supports these constraints natively. CP-SAT includes an LP-propagator but relies on the Dual Simplex algorithm, which is not suitable for these constraints and must depend on simpler methods. Similarly, most open-source MIP solvers may struggle with these constraints.
It is challenging to determine if CP-SAT can handle non-linear expressions efficiently or which solver would be best suited for your problem. Non-linear expressions are invariably complex, and avoiding them when possible is advisable.
Here is one of my students’ favorite examples of a non-linear expression that can be avoided. Once introduced to mathematical notation like \( \sum_{e \in E} cost(e)\cdot x_e \), if a term depends on the combination of two binary variables, they might initially opt for a quadratic expression such as \( \sum_{e,e’\in E} concost(e, e’)\cdot x_e\cdot x_{e’} \). However, such cases can often be modeled linearly using an auxiliary variable, avoiding the complexities of non-linear modeling.
model = cp_model.CpModel()
b1 = model.new_bool_var("b1")
b2 = model.new_bool_var("b2")
b1b2 = model.new_bool_var("b1b2")
model.add_implication(~b1, ~b1b2)
model.add_implication(~b2, ~b1b2)
model.add_bool_or(~b1, ~b2, b1b2) # optional, for a penalty term to be minimized.
There are numerous further instances where non-linear expressions can be simplified by using auxiliary variables or by shifting the non-linear components into constants. However, exploring these techniques is most beneficial when you encounter specific challenges related to non-linear expressions in your models.
We will revisit further discussions on non-linear expressions and their conversion to piecewise linear approximations in a subsequent section. This will provide a foundational understanding necessary for addressing more complex modeling scenarios effectively.
All Different
In various assignment and scheduling problems, ensuring that all variables hold
distinct values is crucial. For example, in frequency assignment, no two
transmitters within the same area should operate on the same frequency, or in
scheduling, no two tasks should occupy the same time slot. Typically, this
requirement could be modeled with a quadratic number of inequality (!=)
constraints. However, a more elegant solution involves using the
add_all_different constraint, which directly enforces that all variables in a
list take unique values. This constraint is particularly useful in solving
puzzles like Sudoku or the
N-queens problem.
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
# Adding an all-different constraint
model.add_all_different([x, y, z])
# Advanced usage with transformations
vars = [model.new_int_var(0, 10, f"v_{i}") for i in range(10)]
model.add_all_different([x + i for i, x in enumerate(vars)])
Using add_all_different not only simplifies the modeling but also utilizes a
dedicated domain-based propagator in CP-SAT, enhancing efficiency beyond what is
achievable with multiple != constraints. However, if your model mixes !=
constraints with add_all_different, be cautious, as CP-SAT disables automatic
inference of add_all_different from groups of != constraints, which can lead
to performance penalties.
For a practical demonstration, refer to the
graph coloring problem example
in our repository. Here, using != constraints solved the problem in seconds,
whereas add_all_different took significantly longer, illustrating the
importance of choosing the right method based on the problem scale and
complexity.
Alternatively, modeling with Boolean variables and constraints like
add_at_most_one or pairwise negations (add_boolean_or(~b1, ~b2)) can also be
effective. This approach benefits from CP-SAT’s efficient handling of Boolean
logic and allows for easy integration of additional constraints or objectives,
such as licensing costs associated with certain frequencies. Although CP-SAT
does something similar internally, it creates these constructs lazily and only
as needed, whereas explicit modeling in Python may not be as efficient.
The choice between these methods—or potentially another strategy—depends on specific model requirements and familiarity with CP-SAT’s behavior. When in doubt, start with the most intuitive method and refine your approach based on performance observations.
Domains and Combinations
When optimizing scenarios with predefined feasible values or combinations of variables—often outlined in a table—it is advantageous to directly restrict the domain of an expression or set of variables.
Consider an example where you are optimizing a shift schedule for a team of employees, and you have a table of feasible combinations for each shift:
| Employee 1 | Employee 2 | Employee 3 | Employee 4 |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
In CP-SAT, this can be modeled efficiently using the add_allowed_assignments
method:
model = cp_model.CpModel()
x_employee_1 = model.new_bool_var("x_employee_1")
x_employee_2 = model.new_bool_var("x_employee_2")
x_employee_3 = model.new_bool_var("x_employee_3")
x_employee_4 = model.new_bool_var("x_employee_4")
# Define the allowed assignments
allowed_assignments = [
[1, 0, 1, 0],
[0, 1, 1, 0],
[1, 0, 0, 1],
[0, 1, 0, 1],
]
model.add_allowed_assignments(
[x_employee_1, x_employee_2, x_employee_3, x_employee_4], allowed_assignments
)
Alternatively, forbidden combinations can be specified using
add_forbidden_assignments:
prohibit_assignments = [
[1, 0, 1, 0],
[0, 1, 1, 0],
[1, 0, 0, 1],
[0, 1, 0, 1],
]
model.add_forbidden_assignments(
[x_employee_1, x_employee_2, x_employee_3, x_employee_4], prohibit_assignments
)
The utility of the add_allowed_assignments method becomes more apparent when
integrated with other constraints within the model, rather than when it spans
all variables. If the table covered all variables, one could theoretically
evaluate each row to identify the best solution without the need for
sophisticated optimization techniques. However, consider this scenario where
constraints are integrated across multiple shifts:
NUM_SHIFTS = 7
model = cp_model.CpModel()
x_employee_1 = [model.new_bool_var(f"x_employee_1_{i}") for i in range(NUM_SHIFTS)]
x_employee_2 = [model.new_bool_var(f"x_employee_2_{i}") for i in range(NUM_SHIFTS)]
x_employee_3 = [model.new_bool_var(f"x_employee_3_{i}") for i in range(NUM_SHIFTS)]
x_employee_4 = [model.new_bool_var(f"x_employee_4_{i}") for i in range(NUM_SHIFTS)]
for i in range(NUM_SHIFTS):
model.add_allowed_assignments(
[x_employee_1[i], x_employee_2[i], x_employee_3[i], x_employee_4[i]],
allowed_assignments,
)
# ... some further constraints and objectives to connect the days ...
# ... if the days would be independent, you would solve each day separately ...
The add_allowed_assignments method in CP-SAT enables the direct incorporation
of specific feasible combinations into your optimization model, ensuring that
only certain configurations of variables are considered within the solution
space. This method effectively “hard-codes” these configurations, simplifying
the model by predefining which combinations of variables are permissible, much
like setting rules for employee shifts or resource allocations.
 Hardcoding specific combinations in your model is a preliminary step toward advanced decomposition techniques like Dantzig-Wolfe decomposition. In this method, a complex optimization problem is simplified by replacing a group of correlated variables with composite variables. Such a composite variable represents a solution for a subproblem. Optimizing these composite variables in the master problem significantly reduces the model’s complexity and improves the efficiency of solving large-scale problems. |
A related method for managing linear expressions instead of direct assignments
is add_linear_expression_in_domain. Suppose we know a certain linear
expression, (10x + 5y), must equal 20, 50, or 100:
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
domain = cp_model.Domain.from_values([20, 50, 100])
model.add_linear_expression_in_domain(10 * x + 5 * y, domain)
 Ensure calculations are correct, especially when working with integers, to
avoid creating an infeasible or overly restrictive model. Consider using an
auxiliary variable with a restricted domain and softer constraints ( |
Element/Array Constraints
Before exploring specialized constraints, let us examine the last of the generic ones. The element constraint facilitates accessing the value of a variable (or since ortools 9.12, a linear expression) within an array using another variable as the index. Accessing a variable in an array with a constant index is straightforward; however, integrating a variable index into your model adds complexity. This constraint can also be used to ensure that a variable matches the value at a specific array position.
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
var_array = [x, y, z]
# Create a variable for the index and a variable for the value at that index.
index_var = model.new_int_var(0, len(var_array) - 1, "index")
value_at_index_var = model.new_int_var(-100, 100, "value_at_index")
# Apply the element constraint to link the index and value variables.
model.add_element(expressions=var_array, index=index_var, target=value_at_index_var)
# CAVEAT: Before ortools 9.12, it was `variables=` instead of `expressions=`.
Examples of feasible variable assignments:
x | y | z | index_var | value_at_index |
|---|---|---|---|---|
| 3 | 4 | 5 | 0 | 3 |
| 3 | 4 | 5 | 1 | 4 |
| 3 | 4 | 5 | 2 | 5 |
| 7 | 3 | 4 | 0 | 7 |
The subsequent constraint resembles a stable matching in array form. For two equally sized arrays of variables \( v \) and \( w \), each of size \( |v| \), it imposes a bijective relationship: \( v[i]=j \Leftrightarrow w[j]=i \) for all \( i,j \in 0,\ldots,|v|-1 \). This constraint limits the variables’ values to \( 0,\ldots, |v|-1 \).
model = cp_model.CpModel()
v = [model.new_int_var(0, 5, f"v_{i}") for i in range(6)]
w = [model.new_int_var(0, 5, f"w_{i}") for i in range(6)]
model.add_inverse(v, w)
Examples of feasible variable assignments:
| array | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| v | 0 | 1 | 2 | 3 | 4 | 5 |
| w | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| v | 1 | 2 | 3 | 4 | 5 | 0 |
| w | 5 | 0 | 1 | 2 | 3 | 4 |
| array | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| v | 1 | 0 | 3 | 5 | 2 | 4 |
| w | 1 | 0 | 4 | 2 | 5 | 3 |
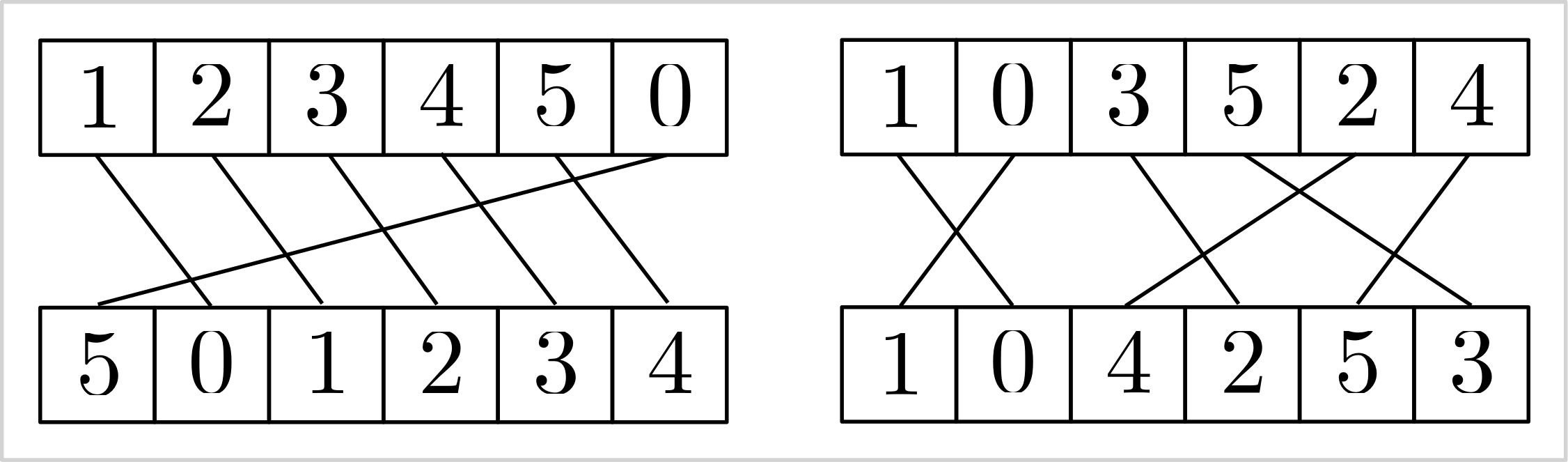 |
|---|
Visualizing the stable matching induced by the add_inverse constraint. |
 I generally advise against using the |
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Advanced Modeling
Advanced Modeling

After having seen the basic elements of CP-SAT, this chapter will introduce you to the more complex constraints. These constraints are already focused on specific problems, such as routing or scheduling, but very generic and powerful within their domain. However, they also need more explanation on the correct usage.
- Tour Constraints:
add_circuit,add_multiple_circuit,add_reservoir_constraint_with_active - Intervals:
new_interval_var,new_interval_var_series,new_fixed_size_interval_var,new_optional_interval_var,new_optional_interval_var_series,new_optional_fixed_size_interval_var,new_optional_fixed_size_interval_var_series,add_no_overlap,add_no_overlap_2d,add_cumulative - Automaton Constraints:
add_automaton - Reservoir Constraints:
add_reservoir_constraint, - Piecewise Linear Constraints: Not officially part of CP-SAT, but we provide some free copy&pasted code to do it.
Circuit/Tour-Constraints
Routes and tours are essential in addressing optimization challenges across
various fields, far beyond traditional routing issues. For example, in DNA
sequencing, optimizing the sequence in which DNA fragments are assembled is
crucial, while in scientific research, methodically ordering the reconfiguration
of experiments can greatly reduce operational costs and downtime. The
add_circuit and add_multiple_circuit constraints in CP-SAT allow you to
easily model various scenarios. These constraints extend beyond the classical
Traveling Salesman Problem (TSP),
allowing for solutions where not every node needs to be visited and
accommodating scenarios that require multiple disjoint sub-tours. This
adaptability makes them invaluable for a broad spectrum of practical problems
where the sequence and arrangement of operations critically impact efficiency
and outcomes.
 |
|---|
| The Traveling Salesman Problem (TSP) asks for the shortest possible route that visits every vertex exactly once and returns to the starting vertex. |
The Traveling Salesman Problem is one of the most famous and well-studied combinatorial optimization problems. It is a classic example of a problem that is easy to understand, common in practice, but hard to solve. It also has a special place in the history of optimization, as many techniques that are now used generally were first developed for the TSP. If you have not done so yet, I recommend watching this talk by Bill Cook, or even reading the book In Pursuit of the Traveling Salesman.
 If your problem is specifically the Traveling Salesperson Problem (TSP), you
might find the
Concorde solver
particularly effective. For problems closely related to the TSP, a Mixed
Integer Programming (MIP) solver may be more suitable, as many TSP variants
yield strong linear programming relaxations that MIP solvers can efficiently
exploit. Additionally, consider
OR-Tools Routing if
routing constitutes a significant aspect of your problem. However, for
scenarios where variants of the TSP are merely a component of a larger
problem, utilizing CP-SAT with the |
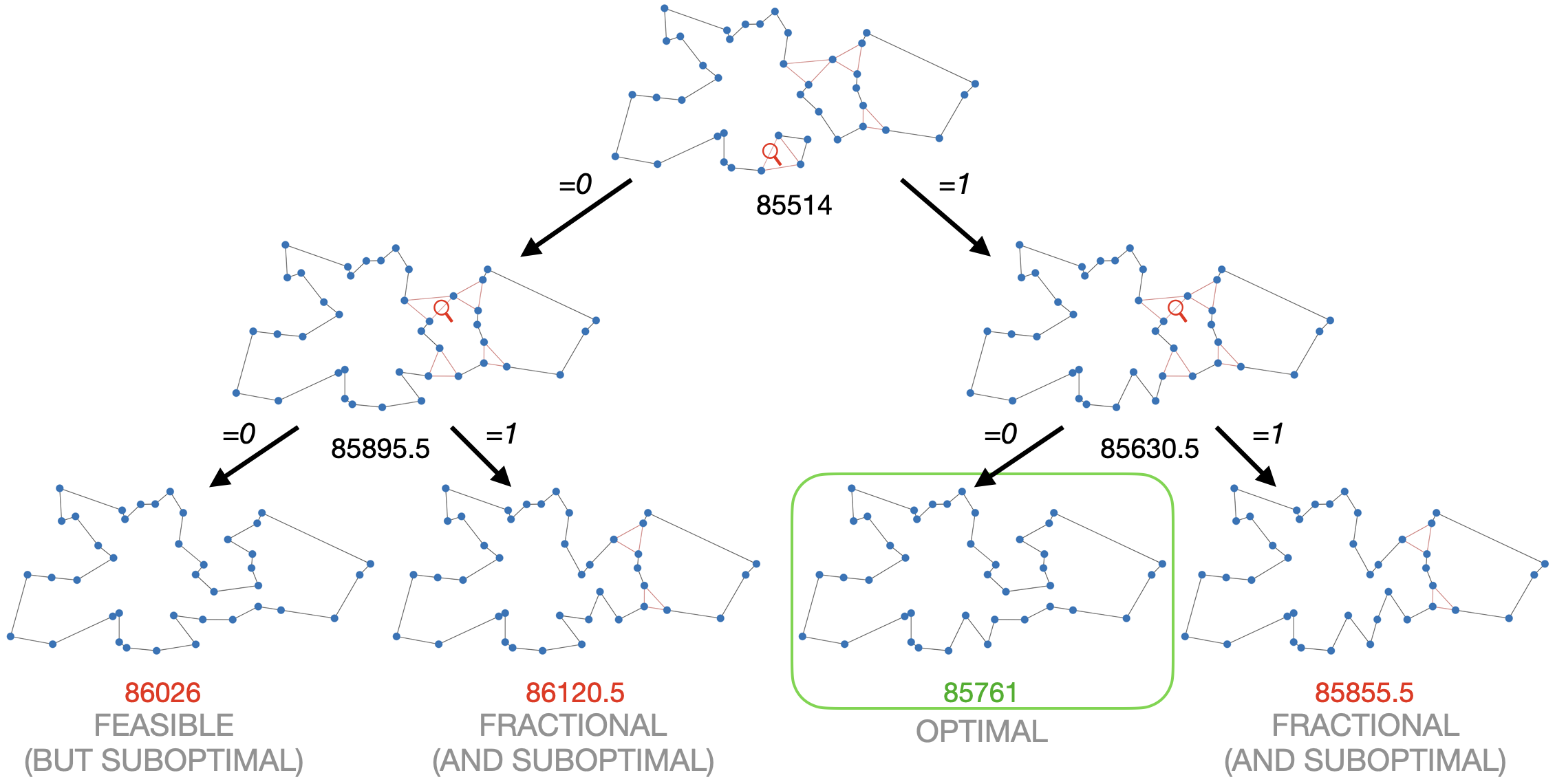 |
|---|
| This example shows why Mixed Integer Programming solvers are so good in solving the TSP. The linear relaxation (at the top) is already very close to the optimal solution. By branching, i.e., trying 0 and 1, on just two fractional variables, we not only find the optimal solution but can also prove optimality. The example was generated with the DIY TSP Solver. |
add_circuit
The add_circuit constraint is utilized to solve circuit problems within
directed graphs, even allowing loops. It operates by taking a list of triples
(u,v,var), where u and v denote the source and target vertices,
respectively, and var is a Boolean variable that indicates if an edge is
included in the solution. The constraint ensures that the edges marked as True
form a single circuit visiting each vertex exactly once, aside from vertices
with a loop set as True. Vertex indices should start at 0 and must not be
skipped to avoid isolation and infeasibility in the circuit.
Here is an example using the CP-SAT solver to address a directed Traveling Salesperson Problem (TSP):
from ortools.sat.python import cp_model
# Directed graph with weighted edges
dgraph = {(0, 1): 13, (1, 0): 17, ...(2, 3): 27}
# Initialize CP-SAT model
model = cp_model.CpModel()
# Boolean variables for each edge
edge_vars = {(u, v): model.new_bool_var(f"e_{u}_{v}") for (u, v) in dgraph.keys()}
# Circuit constraint for a single tour
model.add_circuit([(u, v, var) for (u, v), var in edge_vars.items()])
# Objective function to minimize total cost
model.minimize(sum(dgraph[(u, v)] * x for (u, v), x in edge_vars.items()))
# Solve model
solver = cp_model.CpSolver()
status = solver.solve(model)
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
tour = [(u, v) for (u, v), x in edge_vars.items() if solver.value(x)]
print("Tour:", tour)
# Output: [(0, 1), (2, 0), (3, 2), (1, 3)], i.e., 0 -> 1 -> 3 -> 2 -> 0
This constraint can be adapted for paths by adding a virtual enforced edge that
closes the path into a circuit, such as (3, 0, 1) for a path from vertex 0 to
vertex 3.
Creative usage of add_circuit
The add_circuit constraint can be creatively adapted to solve various related
problems. While there are more efficient algorithms for solving the Shortest
Path Problem, let us demonstrate how to adapt the add_circuit constraint for
educational purposes.
from ortools.sat.python import cp_model
# Define a weighted, directed graph with edge costs
dgraph = {(0, 1): 13, (1, 0): 17, ...(2, 3): 27}
source_vertex = 0
target_vertex = 3
# Add zero-cost loops for vertices not being the source or target
for v in [1, 2]:
dgraph[(v, v)] = 0
# Initialize CP-SAT model and variables
model = cp_model.CpModel()
edge_vars = {(u, v): model.new_bool_var(f"e_{u}_{v}") for (u, v) in dgraph}
# Define the circuit including a pseudo-edge from target to source
circuit = [(u, v, var) for (u, v), var in edge_vars.items()] + [
(target_vertex, source_vertex, 1)
]
model.add_circuit(circuit)
# Minimize total cost
model.minimize(sum(dgraph[(u, v)] * x for (u, v), x in edge_vars.items()))
# Solve and extract the path
solver = cp_model.CpSolver()
status = solver.solve(model)
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
path = [(u, v) for (u, v), x in edge_vars.items() if solver.value(x) and u != v]
print("Path:", path)
# Output: [(0, 1), (1, 3)], i.e., 0 -> 1 -> 3
This approach showcases the flexibility of the add_circuit constraint for
various tour and path problems. Explore further examples:
- Budget constrained tours: Optimize the largest possible tour within a specified budget.
add_multiple_circuit
When solving problems involving multiple trips starting from a depot, we can use
the add_multiple_circuit constraint. This constraint is similar to
add_circuit but explicitly allows the depot to be visited multiple times. Like
add_circuit, the add_multiple_circuit constraint supports optional vertices
through self-loops.
This feature is particularly useful for modeling Vehicle Routing Problems (VRP),
where multiple tours originate from a single depot. Usually, VRP includes
additional constraints since, otherwise, returning to the depot unnecessarily is
suboptimal. While duplicating the graph and applying add_circuit on each copy
is an alternative, using add_multiple_circuit avoids the need for multiple
graph copies and corresponding variable sets, allowing a single set of variables
and edges.
A disadvantage of this method is that expressing certain constraints, such as prohibiting two nodes from being visited during the same trip, becomes more complex since all trips share variables. Nevertheless, many constraints can still be modeled effectively, such as vehicle capacity in the Capacitated Vehicle Routing Problem (CVRP). The CVRP is a classical optimization problem in operations research and logistics, which involves determining the shortest possible set of routes for a fleet of identical vehicles starting and ending at a single depot (this can also be the same vehicle doing multiple trips). Each customer must be visited exactly once, with the constraint that the total demand serviced on each trip does not exceed the vehicle capacity.
The following code illustrates implementing the CVRP using the
add_multiple_circuit constraint by introducing an additional variable to track
vehicle capacity at each vertex.
from typing import Hashable
import networkx as nx
from ortools.sat.python import cp_model
class CvrpMultiCircuit:
"""CVRP via CP-SAT multi-circuit constraint."""
def __init__(
self,
graph: nx.Graph,
depot: Hashable,
capacity: int,
demand_label: str = "demand",
model: cp_model.CpModel | None = None,
):
self.graph, self.depot = graph, depot
self.model = model or cp_model.CpModel()
self.capacity = capacity
self.demand_label = demand_label
# Vertex list with depot first
self.vertices = [depot] + [v for v in graph.nodes() if v != depot]
self.index = {v: i for i, v in enumerate(self.vertices)}
# Boolean arc variables for both directions
self.arc_vars = {
(i, j): self.model.new_bool_var(f"arc_{i}_{j}")
for u, v in graph.edges
for i, j in ((self.index[u], self.index[v]), (self.index[v], self.index[u]))
}
arcs = [(i, j, var) for (i, j), var in self.arc_vars.items()]
# Multi-circuit constraint
self.model.add_multiple_circuit(arcs)
# Capacity variables and constraints
self.cap_vars = [
self.model.new_int_var(0, capacity, f"cap_{i}")
for i in range(len(self.vertices))
]
for i, j, var in arcs:
if j == 0:
continue
demand = graph.nodes[self.vertices[j]].get(demand_label, 0)
self.model.add(
self.cap_vars[j] >= self.cap_vars[i] + demand
).only_enforce_if(var)
def is_arc_used(self, u, v) -> cp_model.BoolVarT:
return self.arc_vars[(self.index[u], self.index[v])]
def weight(self, label: str = "weight") -> cp_model.LinearExprT:
return sum(
var * self.graph[self.vertices[i]][self.vertices[j]][label]
for (i, j), var in self.arc_vars.items()
)
def minimize_weight(self, label: str = "weight"):
self.model.minimize(self.weight(label=label))
def extract_tours(self, solver: cp_model.CpSolver) -> list[list]:
# Build directed graph of selected arcs
dg = nx.DiGraph(
[
(self.vertices[i], self.vertices[j])
for (i, j), var in self.arc_vars.items()
if solver.value(var)
]
)
# Eulerian circuit and split at depot
euler = nx.eulerian_circuit(dg, source=self.depot)
tours, curr = [], [self.depot]
for u, v in euler:
curr.append(v)
if v == self.depot:
tours.append(curr)
curr = [self.depot]
if len(curr) > 1:
tours.append(curr)
return tours
 |
|---|
| The Capacitated Vehicle Routing Problem (CVRP) seeks the shortest possible routes that visit every vertex exactly once and return to the starting vertex. The depot acts as the starting and ending point of each tour. The example graph is weighted by roughly its geometric distance, with a vehicle capacity constraint set to 15. |
 Although the |
Performance of add_circuit for the TSP
The table below displays the performance of the CP-SAT solver on various
instances of the TSPLIB, using the add_circuit constraint, under a 90-second
time limit. The performance can be considered reasonable, but can be easily
beaten by a Mixed Integer Programming solver.
| Instance | # vertices | runtime | lower bound | objective | opt. gap |
|---|---|---|---|---|---|
| att48 | 48 | 0.47 | 33522 | 33522 | 0 |
| eil51 | 51 | 0.69 | 426 | 426 | 0 |
| st70 | 70 | 0.8 | 675 | 675 | 0 |
| eil76 | 76 | 2.49 | 538 | 538 | 0 |
| pr76 | 76 | 54.36 | 108159 | 108159 | 0 |
| kroD100 | 100 | 9.72 | 21294 | 21294 | 0 |
| kroC100 | 100 | 5.57 | 20749 | 20749 | 0 |
| kroB100 | 100 | 6.2 | 22141 | 22141 | 0 |
| kroE100 | 100 | 9.06 | 22049 | 22068 | 0 |
| kroA100 | 100 | 8.41 | 21282 | 21282 | 0 |
| eil101 | 101 | 2.24 | 629 | 629 | 0 |
| lin105 | 105 | 1.37 | 14379 | 14379 | 0 |
| pr107 | 107 | 1.2 | 44303 | 44303 | 0 |
| pr124 | 124 | 33.8 | 59009 | 59030 | 0 |
| pr136 | 136 | 35.98 | 96767 | 96861 | 0 |
| pr144 | 144 | 21.27 | 58534 | 58571 | 0 |
| kroB150 | 150 | 58.44 | 26130 | 26130 | 0 |
| kroA150 | 150 | 90.94 | 26498 | 26977 | 2% |
| pr152 | 152 | 15.28 | 73682 | 73682 | 0 |
| kroA200 | 200 | 90.99 | 29209 | 29459 | 1% |
| kroB200 | 200 | 31.69 | 29437 | 29437 | 0 |
| pr226 | 226 | 74.61 | 80369 | 80369 | 0 |
| gil262 | 262 | 91.58 | 2365 | 2416 | 2% |
| pr264 | 264 | 92.03 | 49121 | 49512 | 1% |
| pr299 | 299 | 92.18 | 47709 | 49217 | 3% |
| linhp318 | 318 | 92.45 | 41915 | 52032 | 19% |
| lin318 | 318 | 92.43 | 41915 | 52025 | 19% |
| pr439 | 439 | 94.22 | 105610 | 163452 | 35% |
There are two prominent formulations to model the Traveling Salesman Problem
(TSP) without an add_circuit constraint: the
Dantzig-Fulkerson-Johnson (DFJ) formulation
and the
Miller-Tucker-Zemlin (MTZ) formulation.
The DFJ formulation is generally regarded as more efficient due to its stronger
linear relaxation. However, it requires lazy constraints, which are not
supported by the CP-SAT solver. When implemented without lazy constraints, the
performance of the DFJ formulation is comparable to that of the MTZ formulation
in CP-SAT. Nevertheless, both formulations perform significantly worse than the
add_circuit constraint. This indicates the superiority of using the
add_circuit constraint for handling tours and paths in such problems. Unlike
end users, the add_circuit constraint can utilize lazy constraints internally,
offering a substantial advantage in solving the TSP.
Scheduling and Packing with Intervals
A special case of variables are the interval variables, that allow to model intervals, i.e., a span of some length with a start and an end. There are fixed length intervals, flexible length intervals, and optional intervals to model various use cases. These intervals become interesting in combination with the no-overlap constraints for 1D and 2D. We can use this for geometric packing problems, scheduling problems, and many other problems, where we have to prevent overlaps between intervals. These variables are special because they are actually not a variable, but a container that bounds separately defined start, length, and end variables.
There are four types of interval variables: new_interval_var,
new_fixed_size_interval_var, new_optional_interval_var, and
new_optional_fixed_size_interval_var. The new_optional_interval_var is the
most expressive but also the most expensive, while new_fixed_size_interval_var
is the least expressive and the easiest to optimize. All four types take a
start= variable. Intervals with fixed_size in their name require a constant
size= argument defining the interval length. Otherwise, the size= argument
can be a variable in combination with an end= variable, which complicates the
solution. Intervals with optional in their name include an is_present=
argument, a boolean indicating if the interval is present. The no-overlap
constraints, discussed later, apply only to intervals that are present, allowing
for modeling problems with multiple resources or optional tasks. Instead of a
pure integer variable, all arguments also accept an affine expression, e.g.,
start=5*start_var+3.
model = cp_model.CpModel()
start_var = model.new_int_var(0, 100, "start")
length_var = model.new_int_var(10, 20, "length")
end_var = model.new_int_var(0, 100, "end")
is_present_var = model.new_bool_var("is_present")
# creating an interval whose length can be influenced by a variable (more expensive)
flexible_interval = model.new_interval_var(
start=start_var, size=length_var, end=end_var, name="flexible_interval"
)
# creating an interval of fixed length
fixed_interval = model.new_fixed_size_interval_var(
start=start_var,
size=10, # needs to be a constant
name="fixed_interval",
)
# creating an interval that can be present or not and whose length can be influenced by a variable (most expensive)
optional_interval = model.new_optional_interval_var(
start=start_var,
size=length_var,
end=end_var,
is_present=is_present_var,
name="optional_interval",
)
# creating an interval that can be present or not
optional_fixed_interval = model.new_optional_fixed_size_interval_var(
start=start_var,
size=10, # needs to be a constant
is_present=is_present_var,
name="optional_fixed_interval",
)
These interval variables are not useful on their own, as we could have easily achieved the same with a simple linear constraint. However, CP-SAT provides special constraints for these interval variables, that would actually be much harder to model by hand and are also much more efficient.
CP-SAT offers the following three constraints for intervals:
add_no_overlap,add_no_overlap_2d, add_cumulative. add_no_overlap is used
to prevent overlaps between intervals on a single dimension, e.g., time.
add_no_overlap_2d is used to prevent overlaps between intervals on two
dimensions, e.g., for packing rectangles. add_cumulative is used to model a
resource constraint, where the sum of the demands of the overlapping intervals
must not exceed the capacity of the resource.
The add_no_overlap constraints takes a list of (optional) interval variables
and ensures that no two present intervals overlap.
model.add_no_overlap(
interval_vars=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
# ...
]
)
The add_no_overlap_2d constraints takes two lists of (optional) interval and
ensures that for every i and j either x_intervals[i] and x_intervals[j]
or y_intervals[i] and y_intervals[j] do not overlap. Thus, both lists must
have the same length as x_intervals[i] and y_intervals[i] are considered
belonging together. If either x_intervals[i] or y_intervals[i] are optional,
the whole object is optional.
model.add_no_overlap_2d(
x_intervals=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
# ...
],
y_intervals=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
# ...
],
)
The add_cumulative constraint is used to model a resource constraint, where
the sum of the demands of the overlapping intervals must not exceed the capacity
of the resource. An example could be scheduling the usage of certain energy
intensive machines, where the sum of the energy demands must not exceed the
capacity of the power grid. It takes a list of intervals, a list of demands, and
a capacity variable. The list of demands must have the same length as the list
of intervals, as the demands of the intervals are matched by index. As capacity
and demands can be variables (or affine expressions), quite complex resource
constraints can be modeled.
demand_vars = [model.new_int_var(1, 10, f"demand_{i}") for i in range(4)]
capacity_var = model.new_int_var(1, 100, "capacity")
model.add_cumulative(
intervals=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
],
demands=demand_vars,
capacity=capacity_var,
)
 Do not directly jump to intervals when you have a scheduling problem.
Intervals are great if you actually have a somewhat continuous time or space
that you need to schedule. If you have a more discrete problem, such as a
scheduling problem with a fixed number of slots, you can often model this
problem much more efficiently using simple Boolean variables and constraints.
Especially if you can use domain knowledge to find clusters of meetings that
cannot overlap, this can be much more efficient. If the scheduling is
dominated by the transitions, your scheduling problem may actually be a
routing problems, for which the |
Let us examine a few examples of how to use these constraints effectively.
Scheduling for a Conference Room with Intervals
Assume we have a conference room and need to schedule several meetings. Each
meeting has a fixed length and a range of possible start times. The time slots
are in 5-minute intervals starting at 8:00 AM and ending at 6:00 PM. Thus, there
are \( 10 \times 12 = 120 \) time slots, and we can use a simple integer variable to
model the start time. With fixed meeting lengths, we can use the
new_fixed_size_interval_var to model the intervals. The add_no_overlap
constraint ensures no two meetings overlap, and domains for the start time can
model the range of possible start times.
To handle input data, let us define a namedtuple to store the meeting and two
functions to convert between time and index.
# Convert time to index and back
def t_to_idx(hour, minute):
return (hour - 8) * 12 + minute // 5
def idx_to_t(time_idx):
hour = 8 + time_idx // 12
minute = (time_idx % 12) * 5
return f"{hour}:{minute:02d}"
# Define meeting information using namedtuples
MeetingInfo = namedtuple("MeetingInfo", ["start_times", "duration"])
Then let us create a few meetings we want to schedule.
# Meeting definitions
meetings = {
"meeting_a": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(12, 0)],
[t_to_idx(16, 0), t_to_idx(17, 0)],
],
duration=120 // 5, # 2 hours
),
"meeting_b": MeetingInfo(
start_times=[
[t_to_idx(10, 0), t_to_idx(12, 0)],
],
duration=30 // 5, # 30 minutes
),
"meeting_c": MeetingInfo(
start_times=[
[t_to_idx(16, 0), t_to_idx(17, 0)],
],
duration=15 // 5, # 15 minutes
),
"meeting_d": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(10, 0)],
[t_to_idx(12, 0), t_to_idx(14, 0)],
],
duration=60 // 5, # 1 hour
),
}
Now we can create the CP-SAT model and add the intervals and constraints.
# Create a new CP-SAT model
model = cp_model.CpModel()
# Create start time variables for each meeting
start_time_vars = {
meeting_name: model.new_int_var_from_domain(
cp_model.Domain.from_intervals(meeting_info.start_times),
f"start_{meeting_name}",
)
for meeting_name, meeting_info in meetings.items()
}
# Create interval variables for each meeting
interval_vars = {
meeting_name: model.new_fixed_size_interval_var(
start=start_time_vars[meeting_name],
size=meeting_info.duration,
name=f"interval_{meeting_name}",
)
for meeting_name, meeting_info in meetings.items()
}
# Ensure that now two meetings overlap
model.add_no_overlap(list(interval_vars.values()))
And finally, we can solve the model and extract the solution.
# Solve the model
solver = cp_model.CpSolver()
status = solver.solve(model)
# Extract and print the solution
scheduled_times = {}
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
for meeting_name in meetings:
start_time = solver.value(start_time_vars[meeting_name])
scheduled_times[meeting_name] = start_time
print(f"{meeting_name} starts at {idx_to_t(start_time)}")
else:
print("No feasible solution found.")
Doing some quick magic with matplotlib, we can visualize the schedule.
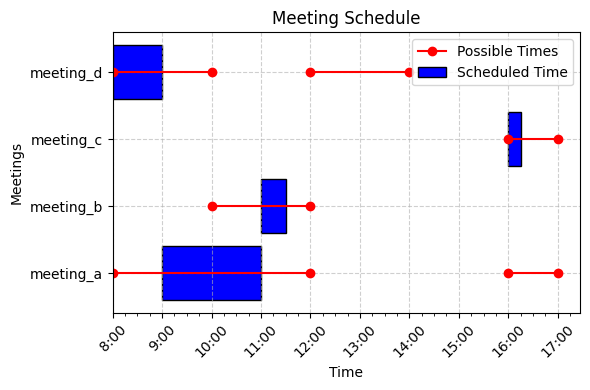 |
|---|
| A possible non-overlapping schedule for the above example. The instance is quite simple, but you could try adding some more meetings. |
Scheduling for Multiple Resources with Optional Intervals
Now, imagine we have multiple resources, such as multiple conference rooms, and
we need to schedule the meetings such that no two meetings overlap in the same
room. This can be modeled with optional intervals, where the intervals exist
only if the meeting is scheduled in the room. The add_no_overlap constraint
ensures that no two meetings overlap in the same room.
Because we now have two rooms, we need to create a more challenging instance first. Otherwise, the solver may not need to use both rooms. We do this by simply adding more and longer meetings.
# Meeting definitions
meetings = {
"meeting_a": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(12, 0)],
[t_to_idx(16, 0), t_to_idx(16, 0)],
],
duration=120 // 5,
),
"meeting_b": MeetingInfo(
start_times=[[t_to_idx(10, 0), t_to_idx(12, 0)]], duration=240 // 5
),
"meeting_c": MeetingInfo(
start_times=[[t_to_idx(16, 0), t_to_idx(17, 0)]], duration=30 // 5
),
"meeting_d": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(10, 0)],
[t_to_idx(12, 0), t_to_idx(14, 0)],
],
duration=60 // 5,
),
"meeting_e": MeetingInfo(
start_times=[[t_to_idx(10, 0), t_to_idx(12, 0)]], duration=120 // 5
),
"meeting_f": MeetingInfo(
start_times=[[t_to_idx(14, 0), t_to_idx(14, 0)]], duration=240 // 5
),
"meeting_g": MeetingInfo(
start_times=[[t_to_idx(14, 0), t_to_idx(16, 0)]], duration=120 // 5
),
}
This time, we need to create an interval variable for each room and meeting, as well as a Boolean variable indicating if the meeting is scheduled in the room. We cannot use the same interval variable for multiple rooms, as otherwise the interval would be present in both rooms.
# Create the model
model = cp_model.CpModel()
# Create start time and room variables
start_time_vars = {
name: model.new_int_var_from_domain(
cp_model.Domain.from_intervals(info.start_times), f"start_{name}"
)
for name, info in meetings.items()
}
rooms = ["room_a", "room_b"]
room_vars = {
name: {room: model.new_bool_var(f"{name}_in_{room}") for room in rooms}
for name in meetings
}
# Create interval variables and add no-overlap constraint
interval_vars = {
name: {
# We need a separate interval for each room
room: model.new_optional_fixed_size_interval_var(
start=start_time_vars[name],
size=info.duration,
is_present=room_vars[name][room],
name=f"interval_{name}_in_{room}",
)
for room in rooms
}
for name, info in meetings.items()
}
Now we can enforce that each meeting is assigned to exactly one room and that there is no overlap between meetings in the same room.
# Ensure each meeting is assigned to exactly one room
for name, room_dict in room_vars.items():
model.add_exactly_one(room_dict.values())
for room in rooms:
model.add_no_overlap([interval_vars[name][room] for name in meetings])
Again, doing some quick magic with matplotlib, we get the following schedule.
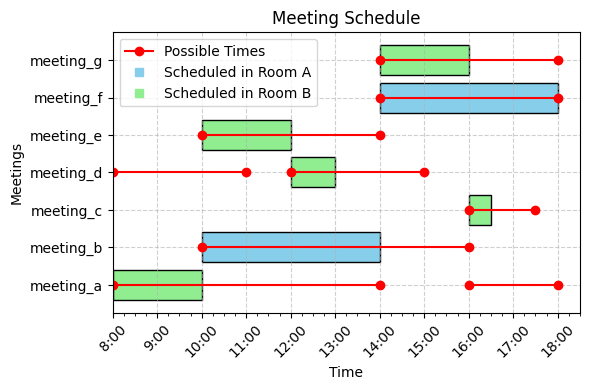 |
|---|
| A possible non-overlapping schedule for the above example with multiple rooms. |
 You could easily extend this model to schedule as many meetings as possible using an objective function. You could also maximize the distance between two meetings by using a variable size interval. This would be a good exercise to try. |
Packing rectangles without overlaps
Let us examine how to check if a set of rectangles can be packed into a container without overlaps. This is a common problem in logistics, where boxes must be packed into a container, or in cutting stock problems, where pieces are cut from a larger material.
First, we define namedtuples for the rectangles and the container.
from collections import namedtuple
# Define namedtuples for rectangles and container
Rectangle = namedtuple("Rectangle", ["width", "height"])
Container = namedtuple("Container", ["width", "height"])
# Example usage
rectangles = [Rectangle(width=2, height=3), Rectangle(width=4, height=5)]
container = Container(width=10, height=10)
Next, we create variables for the bottom-left corners of the rectangles. These variables are constrained to ensure the rectangles remain within the container.
model = cp_model.CpModel()
# Create variables for the bottom-left corners of the rectangles
x_vars = [
model.new_int_var(0, container.width - box.width, name=f"x1_{i}")
for i, box in enumerate(rectangles)
]
y_vars = [
model.new_int_var(0, container.height - box.height, name=f"y1_{i}")
for i, box in enumerate(rectangles)
]
Next, we create interval variables for each rectangle. The start of these
intervals corresponds to the bottom-left corner, and the size is the width or
height of the rectangle. We use the add_no_overlap_2d constraint to ensure
that no two rectangles overlap.
# Create interval variables representing the width and height of the rectangles
x_interval_vars = [
model.new_fixed_size_interval_var(
start=x_vars[i], size=box.width, name=f"x_interval_{i}"
)
for i, box in enumerate(rectangles)
]
y_interval_vars = [
model.new_fixed_size_interval_var(
start=y_vars[i], size=box.height, name=f"y_interval_{i}"
)
for i, box in enumerate(rectangles)
]
# Ensure no two rectangles overlap
model.add_no_overlap_2d(x_interval_vars, y_interval_vars)
The optional intervals with flexible length allow us to model rotations and find the largest possible packing. The code may appear complex, but it remains straightforward considering the problem’s complexity.
First, we define namedtuples for the rectangles and the container.
from collections import namedtuple
from ortools.sat.python import cp_model
# Define namedtuples for rectangles and container
Rectangle = namedtuple("Rectangle", ["width", "height", "value"])
Container = namedtuple("Container", ["width", "height"])
# Example usage
rectangles = [
Rectangle(width=2, height=3, value=1),
Rectangle(width=4, height=5, value=1),
]
container = Container(width=10, height=10)
Next, we create variables for the coordinates of the rectangles. This includes variables for the bottom-left and top-right corners, as well as a boolean variable to indicate if a rectangle is rotated.
model = cp_model.CpModel()
# Create variables for the bottom-left and top-right corners of the rectangles
bottom_left_x_vars = [
model.new_int_var(0, container.width, name=f"x1_{i}")
for i, box in enumerate(rectangles)
]
bottom_left_y_vars = [
model.new_int_var(0, container.height, name=f"y1_{i}")
for i, box in enumerate(rectangles)
]
upper_right_x_vars = [
model.new_int_var(0, container.width, name=f"x2_{i}")
for i, box in enumerate(rectangles)
]
upper_right_y_vars = [
model.new_int_var(0, container.height, name=f"y2_{i}")
for i, box in enumerate(rectangles)
]
# Create variables to indicate if a rectangle is rotated
rotated_vars = [model.new_bool_var(f"rotated_{i}") for i in range(len(rectangles))]
We then create variables for the width and height of each rectangle, adjusting for rotation. Constraints ensure these variables are set correctly based on whether the rectangle is rotated.
# Create variables for the width and height, adjusted for rotation
width_vars = []
height_vars = []
for i, box in enumerate(rectangles):
domain = cp_model.Domain.from_values([box.width, box.height])
width_vars.append(model.new_int_var_from_domain(domain, name=f"width_{i}"))
height_vars.append(model.new_int_var_from_domain(domain, name=f"height_{i}"))
# There are two possible assignments for width and height
model.add_allowed_assignments(
[width_vars[i], height_vars[i], rotated_vars[i]],
[(box.width, box.height, 0), (box.height, box.width, 1)],
)
Next, we create a boolean variable indicating if a rectangle is packed or not, and then interval variables representing its occupied space in the container. These intervals are used to enforce the no-overlap constraint.
# Create variables indicating if a rectangle is packed
packed_vars = [model.new_bool_var(f"packed_{i}") for i in range(len(rectangles))]
# Create interval variables representing the width and height of the rectangles
x_interval_vars = [
model.new_optional_interval_var(
start=bottom_left_x_vars[i],
size=width_vars[i],
is_present=packed_vars[i],
end=upper_right_x_vars[i],
name=f"x_interval_{i}",
)
for i, box in enumerate(rectangles)
]
y_interval_vars = [
model.new_optional_interval_var(
start=bottom_left_y_vars[i],
size=height_vars[i],
is_present=packed_vars[i],
end=upper_right_y_vars[i],
name=f"y_interval_{i}",
)
for i, box in enumerate(rectangles)
]
# Ensure no two rectangles overlap
model.add_no_overlap_2d(x_interval_vars, y_interval_vars)
Finally, we maximize the number of packed rectangles by defining an objective function.
# Maximize the number of packed rectangles
model.maximize(sum(box.value * x for x, box in zip(packed_vars, rectangles)))
 |
|---|
| This dense packing was found by CP-SAT in less than 0.3s, which is quite impressive and seems to be more efficient than a naive Gurobi implementation. |
You can find the full code here:
| Problem Variant | Code |
|---|---|
| Deciding feasibility of packing rectangles without rotations | ./evaluations/packing/solver/packing_wo_rotations.py |
| Finding the largest possible packing of rectangles without rotations | ./evaluations/packing/solver/knapsack_wo_rotations.py |
| Deciding feasibility of packing rectangles with rotations | ./evaluations/packing/solver/packing_with_rotations.py |
| Finding the largest possible packing of rectangles with rotations | ./evaluations/packing/solver/knapsack_with_rotations.py |
CP-SAT is good at finding a feasible packing, but incapable of proving infeasibility in most cases. When using the knapsack variant, it can still pack most of the rectangles even for the larger instances.
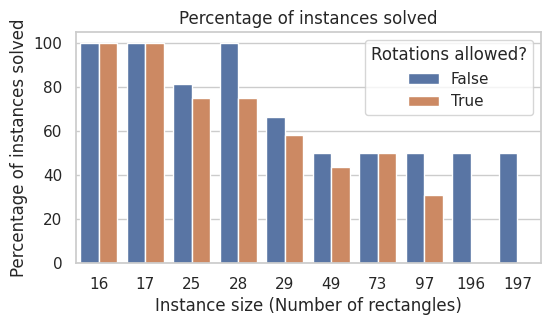 |
|---|
| The number of solved instances for the packing problem (90s time limit). Rotations make things slightly more difficult. None of the used instances were proved infeasible. |
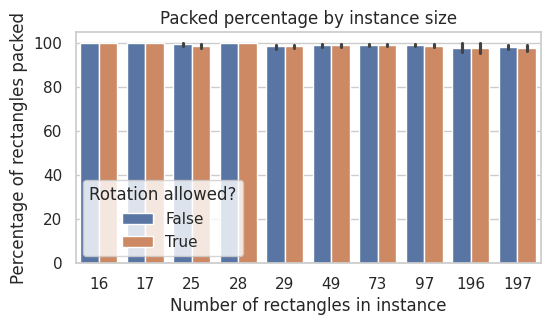 |
| However, CP-SAT is able to pack nearly all rectangles even for the largest instances. |
Resolution and Parameters
In earlier versions of CP-SAT, the performance of no-overlap constraints was greatly influenced by the resolution. This impact has evolved, yet it remains somewhat inconsistent. In a notebook example, I explored how resolution affects the execution time of the no-overlap constraint in versions 9.3 and 9.8 of CP-SAT. For version 9.3, there is a noticeable increase in execution time as the resolution grows. Conversely, in version 9.8, execution time actually reduces when the resolution is higher, a finding supported by repeated tests. This unexpected behavior suggests that the performance of CP-SAT regarding no-overlap constraints has not stabilized and may continue to vary in upcoming versions.
| Resolution | Runtime (CP-SAT 9.3) | Runtime (CP-SAT 9.8) |
|---|---|---|
| 1x | 0.02s | 0.03s |
| 10x | 0.7s | 0.02s |
| 100x | 7.6s | 1.1s |
| 1000x | 75s | 40.3s |
| 10_000x | >15min | 0.4s |
This notebook was used to create the table above.
However, while playing around with less documented features, I noticed that the performance for the older version can be improved drastically with the following parameters:
solver.parameters.use_energetic_reasoning_in_no_overlap_2d = True
solver.parameters.use_timetabling_in_no_overlap_2d = True
solver.parameters.use_pairwise_reasoning_in_no_overlap_2d = True
With the latest version of CP-SAT, I did not notice a significant difference in performance when using these parameters.
Automaton Constraints
Automaton constraints model finite state machines, enabling the representation of feasible transitions between states. This is particularly useful in software verification, where it is essential to ensure that a program follows a specified sequence of states. Given the critical importance of verification in research, there is likely a dedicated audience that appreciates this constraint. However, others may prefer to proceed to the next section.
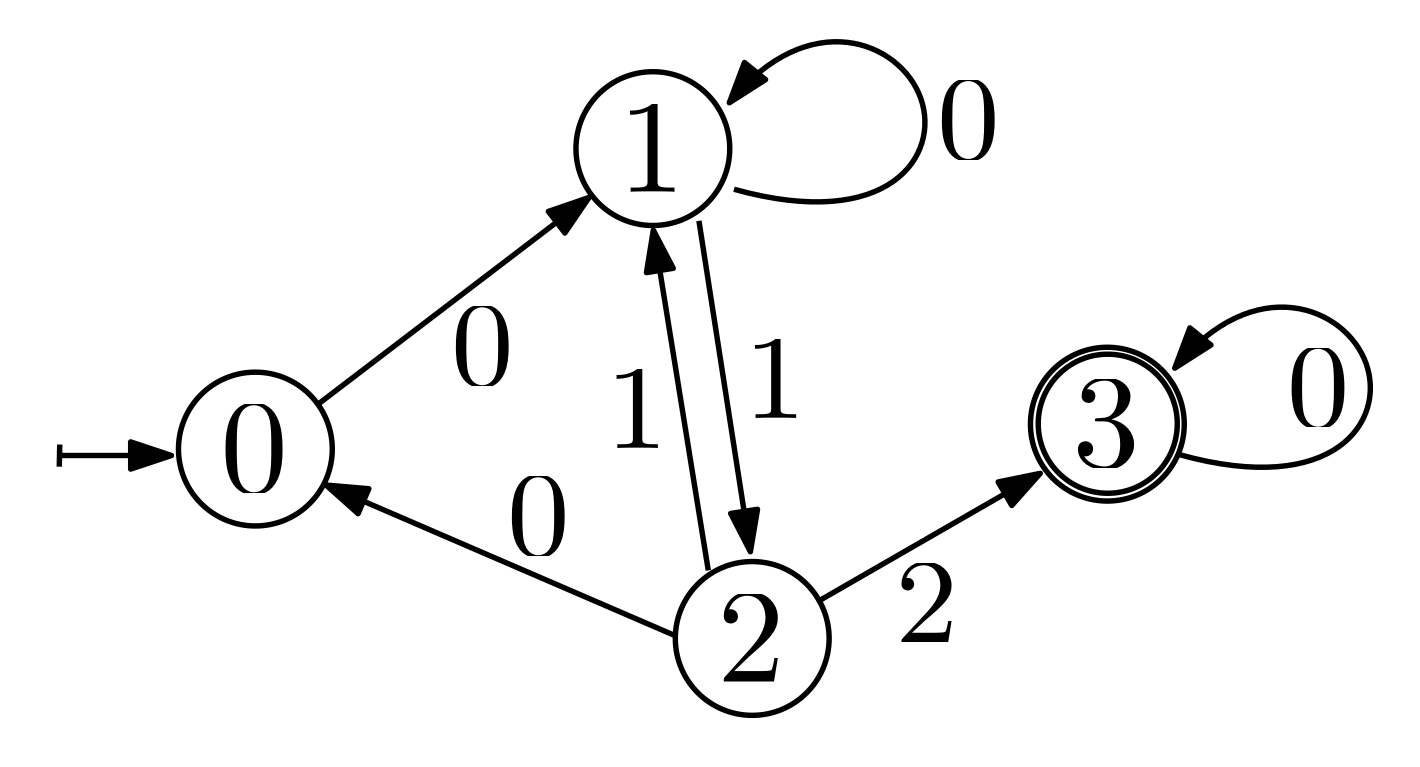 |
|---|
| An example of a finite state machine with four states and seven transitions. State 0 is the initial state, and state 3 is the final state. |
The automaton operates as follows: We have a list of integer variables
transition_variables that represent the transition values. Starting from the
starting_state, the next state is determined by the transition triple
(state, transition_value, next_state) matching the first transition variable.
If no such triple is found, the model is infeasible. This process repeats for
each subsequent transition variable. It is crucial that the final transition
leads to a final state (possibly via a loop); otherwise, the model remains
infeasible.
The state machine from the example can be modeled as follows:
model = cp_model.CpModel()
transition_variables = [model.new_int_var(0, 2, f"transition_{i}") for i in range(4)]
transition_triples = [
(0, 0, 1), # If in state 0 and the transition value is 0, go to state 1
(1, 0, 1), # If in state 1 and the transition value is 0, stay in state 1
(1, 1, 2), # If in state 1 and the transition value is 1, go to state 2
(2, 0, 0), # If in state 2 and the transition value is 0, go to state 0
(2, 1, 1), # If in state 2 and the transition value is 1, go to state 1
(2, 2, 3), # If in state 2 and the transition value is 2, go to state 3
(3, 0, 3), # If in state 3 and the transition value is 0, stay in state 3
]
model.add_automaton(
transition_variables=transition_variables,
starting_state=0,
final_states=[3],
transition_triples=transition_triples,
)
The assignment [0, 1, 2, 0] would be a feasible solution for this model,
whereas the assignment [1, 0, 1, 2] would be infeasible because state 0 has no
transition for value 1. Similarly, the assignment [0, 0, 1, 1] would be
infeasible as it does not end in a final state.
 The automaton constraint is for example used in this paper to model Parallel Batch Scheduling With Incompatible Job Families. |
Reservoir Constraints
Sometimes, we need to keep the balance between inflows and outflows of a
reservoir. The name giving example is a water reservoir, where we need to keep
the water level between a minimum and a maximum level. The reservoir constraint
takes a list of time variables, a list of integer level changes, and the minimum
and maximum level of the reservoir. If the affine expression times[i] is
assigned a value t, then the current level changes by level_changes[i]. Note
that at the moment, variable level changes are not supported, which means level
changes are constant at time t. The constraint ensures that the level stays
between the minimum and maximum level at all time, i.e.
sum(level_changes[i] if times[i] <= t) in [min_level, max_level].
There are many other examples apart from water reservoirs, where you need to
balance demands and supplies, such as maintaining a certain stock level in a
warehouse, or ensuring a certain staffing level in a clinic. The
add_reservoir_constraint constraint in CP-SAT allows you to model such
problems easily.
In the following example, times[i] represents the time at which the change
level_changes[i] will be applied, thus both lists needs to be of the same
length. The reservoir level starts at 0, and the minimum level has to be
\( \leq 0 \) and the maximum level has to be \( \geq 0 \).
times = [model.new_int_var(0, 10, f"time_{i}") for i in range(10)]
level_changes = [1] * 10
model.add_reservoir_constraint(
times=times,
level_changes=level_changes,
min_level=-10,
max_level=10,
)
Additionally, the add_reservoir_constraint_with_active constraint allows you
to model a reservoir with optional changes. Here, we additionally have a list
of Boolean variables actives, where actives[i] indicates if the change
level_changes[i] takes place, i.e. if
sum(level_changes[i] * actives[i] if times[i] <= t) in [min_level, max_level]
If a change is not active, it is as if it does not exist, and the reservoir
level remains the same, independent of the time and change values.
times = [model.new_int_var(0, 10, f"time_{i}") for i in range(10)]
level_changes = [1] * 10
actives = [model.new_bool_var(f"active_{i}") for i in range(10)]
model.add_reservoir_constraint_with_active(
times=times,
level_changes=level_changes,
actives=actives,
min_level=-10,
max_level=10,
)
To illustrate the usage of the reservoir constraint, we look at an example for scheduling nurses in a clinic. For the full example, take a look at the notebook.
The clinic needs to ensure that there are always enough nurses available without over-staffing too much. For a 12-hour work day, we model the demands for nurses as integers for each hour of the day.
# a positive number means we need more nurses, a negative number means we need fewer nurses.
demand_change_at_t = [3, 0, 0, 0, 2, 0, 0, 0, -1, 0, -1, 0, -3]
demand_change_times = list(range(len(demand_change_at_t))) # [0, 1, ..., 12]
We have a list of nurses, each with an individual availability as well as a maximum shift length.
max_shift_length = 5
# begin and end of the availability of each nurse
nurse_availabilities = 2 * [
(0, 7),
(0, 4),
(0, 8),
(2, 9),
(1, 5),
(5, 12),
(7, 12),
(0, 12),
(4, 12),
]
We now initialize all relevant variables of the model. Each nurse is assigned a start and end time of their shift as well as a Boolean variable indicating if they are working at all.
# boolean variable to indicate if a nurse is scheduled
nurse_scheduled = [
model.new_bool_var(f"nurse_{i}_scheduled") for i in range(len(nurse_availabilities))
]
# model the begin and end of each shift
shifts_begin = [
model.new_int_var(begin, end, f"begin_nurse_{i}")
for i, (begin, end) in enumerate(nurse_availabilities)
]
shifts_end = [
model.new_int_var(begin, end, f"end_nurse_{i}")
for i, (begin, end) in enumerate(nurse_availabilities)
]
We now add some basic constraints to ensure that the shifts are valid.
for begin, end in zip(shifts_begin, shifts_end):
model.add(end >= begin) # make sure the end is after the begin
model.add(end - begin <= max_shift_length) # make sure, the shifts are not too long
Our reservoir level is the number of nurses scheduled at any time minus the demand for nurses up until that point. We can now add the reservoir constraint to ensure that we have enough nurses available at all times while not having too many nurses scheduled (i.e., the reservoir level is between 0 and 2). We have three types of changes in the reservoir:
- The demand for nurses changes at the beginning of each hour. For these we use fixed integer times and activate all changes. Note that the demand changes are negated, as an increase in demand lowers the reservoir level.
- If a nurse begins a shift, we increase the reservoir level by 1. We use the
shifts_beginvariables as times and change the reservoir level only if the nurse is scheduled. - Once a nurse ends a shift, we decrease the reservoir level by 1. We use the
shifts_endvariables as times and change the reservoir level only if the nurse is scheduled.
times = demand_change_times
demands = [
-demand for demand in demand_change_at_t
] # an increase in demand lowers the reservoir
actives = [1] * len(demand_change_times)
times += list(shifts_begin)
demands += [1] * len(shifts_begin) # a nurse begins a shift
actives += list(nurse_scheduled)
times += list(shifts_end)
demands += [-1] * len(shifts_end) # a nurse ends a shift
actives += list(nurse_scheduled)
model.add_reservoir_constraint_with_active(
times=times,
level_changes=demands,
min_level=0,
max_level=2,
actives=actives,
)
 The reservoir constraints can express conditions that are difficult to model “by hand”. However, while I do not have much experience with them, I would not expect them to be particularly easy to optimize. Let me know if you have either good or bad experiences with them in practice and for which problem scales they work well. |
Non-Linear Constraints/Piecewise Linear Functions
In practice, you often have cost functions that are not linear. For example, consider a production problem where you have three different items you produce. Each item has different components, you have to buy. The cost of the components will first decrease with the amount you buy, then at some point increase again as your supplier will be out of stock and you have to buy from a more expensive supplier. Additionally, you only have a certain amount of customers willing to pay a certain price for your product. If you want to sell more, you will have to lower the price, which will decrease your profit.
Let us assume such a function looks like \( y=f(x) \) in the following figure. Unfortunately, it is a rather complex function that we cannot directly express in CP-SAT. However, we can approximate it with a piecewise linear function as shown in red. Such piecewise linear approximations are very common, and some solvers can even do them automatically, e.g., Gurobi. The resolution can be arbitrarily high, but the more segments you have, the more complex the model becomes. Thus, it is usually only chosen to be as high as necessary.
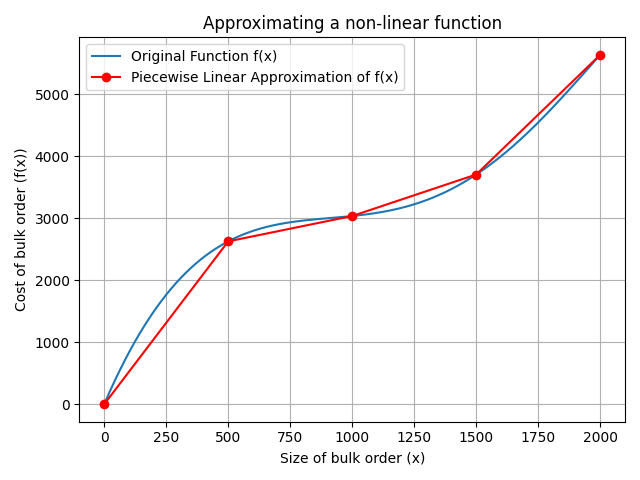 |
|---|
| We can model an arbitrary continuous function with a piecewise linear function. Here, we split the original function into a number of straight segments. The accuracy can be adapted to the requirements. The linear segments can then be expressed in CP-SAT. The fewer such segments, the easier it remains to model and solve. |
Using linear constraints (model.add) and reification (.only_enforce_if), we
can model such a piecewise linear function in CP-SAT. For this we simply use
boolean variables to decide for a segment, and then activate the corresponding
linear constraint via reification. However, this has two problems in CP-SAT, as
shown in the next figure.
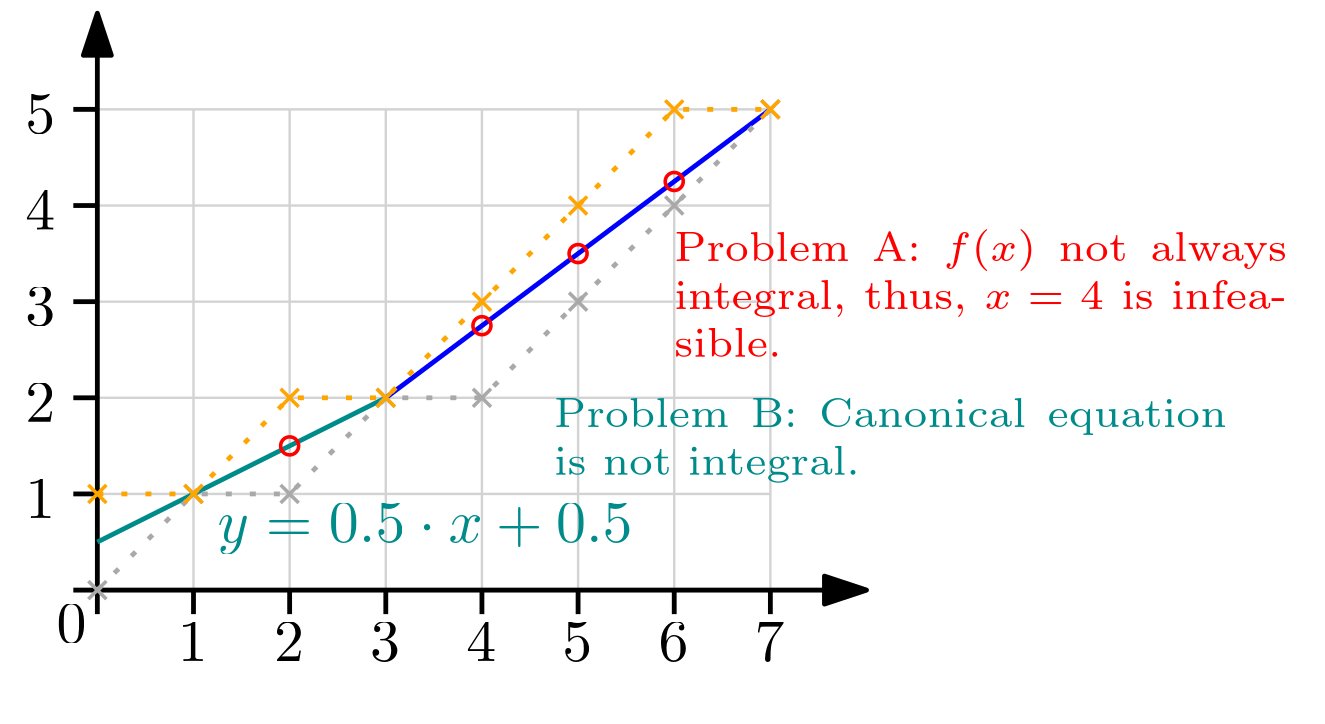 |
|---|
| Even if the function f(x) now consists of linear segments, we cannot simply implement \( y=f(x) \) in CP-SAT. First, for many \( x \)-values, \( f(x) \) will be not integral and, thus, infeasible. Second, the canonical representation of many linear segments will require non-integral coefficients, which are also not allowed in CP-SAT. |
-
Problem A: Even if we can express a segment as a linear function, the result of the function may not be integral. In the example, \( f(5) \) would be \( 3.5 \) and, thus, if we enforce \( y=f(x) \), \( x \) would be prohibited to be \( 5 \), which is not what we want. There are two options now. Either, we use a more complex piecewise linear approximation that ensures that the function will always yield integral solutions or we use inequalities instead. The first solution has the issue that this can require too many segments, making it far too expensive to optimize. The second solution will be a weaker constraint as now we can only enforce \( y<=f(x) \) or \( y>=f(x) \), but not \( y=f(x) \). If you try to enforce it by \( y<=f(x) \) and \( y>=f(x) \), you will end with the same infeasibility as before. However, often an inequality will be enough. If the problem is to prevent \( y \) from becoming too large, you use \( y<=f(x) \), if the problem is to prevent \( y \) from becoming too small, you use \( y>=f(x) \). If we want to represent the costs by \( f(x) \), we would use \( y>=f(x) \) to minimize the costs.
-
Problem B: The canonical representation of a linear function is \( y=ax+b \). However, this will often require non-integral coefficients. Luckily, we can automatically scale them up to integral values by adding a scaling factor. The inequality \( y=0.5x+0.5 \) in the example can also be represented as \( 2y=x+1 \). I will spare you the math, but it just requires a simple trick with the least common multiple. Of course, the required scaling factor can become large, and at some point lead to overflows.
An implementation could now look as follows:
# We want to enforce y=f(x)
x = model.new_int_var(0, 7, "x")
y = model.new_int_var(0, 5, "y")
# use boolean variables to decide for a segment
segment_active = [model.new_bool_var("segment_1"), model.new_bool_var("segment_2")]
model.add_at_most_one(segment_active) # enforce one segment to be active
# Segment 1
# if 0<=x<=3, then y >= 0.5*x + 0.5
model.add(2 * y >= x + 1).only_enforce_if(segment_active[0])
model.add(x >= 0).only_enforce_if(segment_active[0])
model.add(x <= 3).only_enforce_if(segment_active[0])
# Segment 2
model.add(_SLIGHTLY_MORE_COMPLEX_INEQUALITY_).only_enforce_if(segment_active[1])
model.add(x >= 3).only_enforce_if(segment_active[1])
model.add(x <= 7).only_enforce_if(segment_active[1])
model.minimize(y)
# if we were to maximize y, we would have used <= instead of >=
This can be quite tedious, but luckily, I wrote a small helper class that will do this automatically for you. You can find it in ./utils/piecewise_functions. Simply copy it into your code.
This code does some further optimizations:
- Considering every segment as a separate case can be quite expensive and inefficient. Thus, it can make a serious difference if you can combine multiple segments into a single case. This can be achieved by detecting convex ranges, as the constraints of convex areas do not interfere with each other.
- Adding the convex hull of the segments as a redundant constraint that does
not depend on any
only_enforce_ifcan in some cases help the solver to find better bounds.only_enforce_if-constraints are often not very good for the linear relaxation, and having the convex hull as independent constraint can directly limit the solution space, without having to do any branching on the cases.
Let us use this code to solve an instance of the problem above.
We have two products that each require three components. The first product requires 3 of component 1, 5 of component 2, and 2 of component 3. The second product requires 2 of component 1, 1 of component 2, and 3 of component 3. We can buy up to 1500 of each component for the price given in the figure below. We can produce up to 300 of each product and sell them for the price given in the figure below.
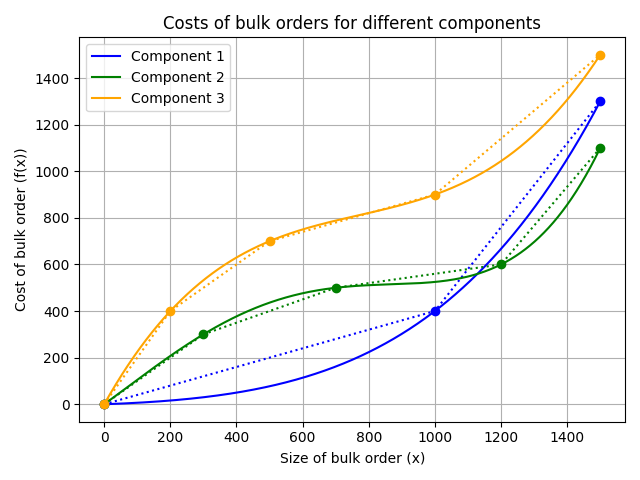 |  |
|---|---|
| Costs for buying components necessary for production. | Selling price for the products. |
We want to maximize the profit, i.e., the selling price minus the costs for buying the components. We can model this as follows:
requirements_1 = (3, 5, 2)
requirements_2 = (2, 1, 3)
from ortools.sat.python import cp_model
model = cp_model.CpModel()
buy_1 = model.new_int_var(0, 1_500, "buy_1")
buy_2 = model.new_int_var(0, 1_500, "buy_2")
buy_3 = model.new_int_var(0, 1_500, "buy_3")
produce_1 = model.new_int_var(0, 300, "produce_1")
produce_2 = model.new_int_var(0, 300, "produce_2")
model.add(produce_1 * requirements_1[0] + produce_2 * requirements_2[0] <= buy_1)
model.add(produce_1 * requirements_1[1] + produce_2 * requirements_2[1] <= buy_2)
model.add(produce_1 * requirements_1[2] + produce_2 * requirements_2[2] <= buy_3)
# You can find this code it ./utils!
from piecewise_functions import PiecewiseLinearFunction, PiecewiseLinearConstraint
# Define the functions for the costs
costs_1 = [(0, 0), (1000, 400), (1500, 1300)]
costs_2 = [(0, 0), (300, 300), (700, 500), (1200, 600), (1500, 1100)]
costs_3 = [(0, 0), (200, 400), (500, 700), (1000, 900), (1500, 1500)]
# PiecewiseLinearFunction is a pydantic model and can be serialized easily!
f_costs_1 = PiecewiseLinearFunction(
xs=[x for x, y in costs_1], ys=[y for x, y in costs_1]
)
f_costs_2 = PiecewiseLinearFunction(
xs=[x for x, y in costs_2], ys=[y for x, y in costs_2]
)
f_costs_3 = PiecewiseLinearFunction(
xs=[x for x, y in costs_3], ys=[y for x, y in costs_3]
)
# Define the functions for the gain
gain_1 = [(0, 0), (100, 800), (200, 1600), (300, 2_000)]
gain_2 = [(0, 0), (80, 1_000), (150, 1_300), (200, 1_400), (300, 1_500)]
f_gain_1 = PiecewiseLinearFunction(xs=[x for x, y in gain_1], ys=[y for x, y in gain_1])
f_gain_2 = PiecewiseLinearFunction(xs=[x for x, y in gain_2], ys=[y for x, y in gain_2])
# Create y>=f(x) constraints for the costs
x_costs_1 = PiecewiseLinearConstraint(model, buy_1, f_costs_1, upper_bound=False)
x_costs_2 = PiecewiseLinearConstraint(model, buy_2, f_costs_2, upper_bound=False)
x_costs_3 = PiecewiseLinearConstraint(model, buy_3, f_costs_3, upper_bound=False)
# Create y<=f(x) constraints for the gain
x_gain_1 = PiecewiseLinearConstraint(model, produce_1, f_gain_1, upper_bound=True)
x_gain_2 = PiecewiseLinearConstraint(model, produce_2, f_gain_2, upper_bound=True)
# Maximize the gain minus the costs
model.Maximize(x_gain_1.y + x_gain_2.y - (x_costs_1.y + x_costs_2.y + x_costs_3.y))
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
status = solver.solve(model)
print(f"Buy {solver.value(buy_1)} of component 1")
print(f"Buy {solver.value(buy_2)} of component 2")
print(f"Buy {solver.value(buy_3)} of component 3")
print(f"Produce {solver.value(produce_1)} of product 1")
print(f"Produce {solver.value(produce_2)} of product 2")
print(f"Overall gain: {solver.objective_value}")
This will give you the following output:
Buy 930 of component 1
Buy 1200 of component 2
Buy 870 of component 3
Produce 210 of product 1
Produce 150 of product 2
Overall gain: 1120.0
Unfortunately, these problems quickly get very complicated to model and solve. This is just a proof that, theoretically, you can model such problems in CP-SAT. Practically, you can lose a lot of time and sanity with this if you are not an expert.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Parameters
Parameters

The CP-SAT solver offers numerous parameters to control its behavior. These
parameters are implemented via
Protocol Buffers and can be
manipulated using the parameters member. To explore all available options,
refer to the well-documented proto file in the
official repository.
Below, I will highlight the most important parameters so you can get the most
out of CP-SAT.
 Only a few parameters, such as |
Logging
The log_search_progress parameter is crucial at the beginning. It enables
logging of the search progress, providing insights into how CP-SAT solves your
problem. While you may deactivate it later for production, it is beneficial
during development to understand the process and respond to any issues.
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
# Custom log function, for example, using the Python logging module instead of stdout
# Useful in a Jupyter notebook, where logging to stdout might not be visible
solver.log_callback = print # (str)->None
# If using a custom log function, you can disable logging to stdout
solver.parameters.log_to_stdout = False
The log offers valuable information for understanding CP-SAT and your optimization problem. It details aspects such as how many variables were directly removed and which techniques most effectively contributed to improving lower and upper bounds.
An example log might look like this:
Starting CP-SAT solver v9.10.4067
Parameters: max_time_in_seconds: 30 log_search_progress: true relative_gap_limit: 0.01
Setting number of workers to 16
Initial optimization model '': (model_fingerprint: 0x1d316fc2ae4c02b1)
#Variables: 450 (#bools: 276 #ints: 6 in objective)
- 342 Booleans in [0,1]
- 12 in [0][10][20][30][40][50][60][70][80][90][100]
- 6 in [0][10][20][30][40][100]
- 6 in [0][80][100]
- 6 in [0][100]
- 6 in [0,1][34][67][100]
- 12 in [0,6]
- 18 in [0,7]
- 6 in [0,35]
- 6 in [0,36]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kBoolOr: 30 (#literals: 72)
#kLinear1: 33 (#enforced: 12)
#kLinear2: 1'811
#kLinear3: 36
#kLinearN: 94 (#terms: 1'392)
Starting presolve at 0.00s
3.26e-04s 0.00e+00d [DetectDominanceRelations]
6.60e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=4 #num_dual_strengthening=3
2.69e-05s 0.00e+00d [ExtractEncodingFromLinear] #potential_supersets=44 #potential_subsets=12
[Symmetry] Graph for symmetry has 2'224 nodes and 5'046 arcs.
[Symmetry] Symmetry computation done. time: 0.000374304 dtime: 0.00068988
[Symmetry] #generators: 2, average support size: 12
[Symmetry] 12 orbits with sizes: 2,2,2,2,2,2,2,2,2,2,...
[Symmetry] Found orbitope of size 6 x 2
[SAT presolve] num removable Booleans: 0 / 309
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [3.0778e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [4.6758e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
1.10e-02s 9.68e-03d [Probe] #probed=1'738 #new_bounds=12 #new_binary_clauses=1'111
2.34e-03s 0.00e+00d [MaxClique] Merged 602(1374 literals) into 506(1960 literals) at_most_ones.
3.31e-04s 0.00e+00d [DetectDominanceRelations]
1.89e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=1
5.45e-04s 0.00e+00d [ProcessAtMostOneAndLinear]
8.19e-04s 0.00e+00d [DetectDuplicateConstraints] #without_enforcements=306
8.62e-05s 7.21e-06d [DetectDominatedLinearConstraints] #relevant_constraints=114 #num_inclusions=42
1.94e-05s 0.00e+00d [DetectDifferentVariables]
1.90e-04s 8.39e-06d [ProcessSetPPC] #relevant_constraints=560 #num_inclusions=24
2.01e-05s 0.00e+00d [FindAlmostIdenticalLinearConstraints]
...
Given the complexity of the log, I developed a tool to visualize and comment on it. You can copy and paste your log into the tool, which will automatically highlight the most important details. Be sure to check out the examples.
 |
|---|
| A plot of the search progress over time as visualized by the log analyzer using information from the log (a different log than displayed above). This plot helps you understand which part of your problem is more challenging: finding a good solution or proving its quality. Based on this, you can implement appropriate countermeasures. |
We will revisit the logs in the next chapter.
 From my experience as a lecturer, I often encounter students who believe CP-SAT is stuck, only to discover that their model building includes an unnecessarily complex \( O(n^5) \) nested loop, which would take days to run. It is natural to assume that the issue lies with CP-SAT because it handles the hard part of solving the problem. However, even the seemingly simple part of model building can consume a lot of time if implemented incorrectly. By enabling logging, students could immediately see that the issue lies in their own code rather than with CP-SAT. This simple step can save a lot of time and frustration. |
Time Limit and Status
When working with large or complex models, the CP-SAT solver may not always reach an optimal solution within a reasonable time frame and could potentially run indefinitely. Therefore, setting a time limit is advisable, particularly in a production environment, to prevent the solver from running endlessly. Even within a time limit, CP-SAT often finds a reasonably good solution, although it may not be proven optimal.
Determining an appropriate time limit depends on various factors and usually requires some experimentation. I typically start with a time limit between 60 and 300 seconds, as this provides a balance between not having to wait too long during model testing and giving the solver enough time to find a good solution.
To set a time limit (in seconds) before running the solver, use the following command:
solver.parameters.max_time_in_seconds = 60 # 60s time limit
After running the solver, it is important to check the status to determine whether an optimal solution, a feasible solution, or no solution at all has been found:
status = solver.solve(model)
if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
print("We have a solution.")
else:
print("Help?! No solution available! :( ")
The possible status codes are:
OPTIMAL(4): An optimal solution has been found.FEASIBLE(2): A feasible solution has been found, and a bound may be available to assess its quality viasolver.best_objective_bound.INFEASIBLE(3): No solution can satisfy all constraints.MODEL_INVALID(1): The CP-SAT model is incorrectly specified.UNKNOWN(0): No solution was found, and no infeasibility proof is available. A bound may still be available.
To get the name from the status code, use solver.status_name(status).
In addition to limiting runtime, you can specify acceptable solution quality
using absolute_gap_limit and relative_gap_limit. The absolute limit stops
the solver when the solution is within a specified value of the bound. The
relative limit stops the solver when the objective value (O) is within a
specified ratio of the bound (B). To stop when the solution is (provably) within
5% of the optimum, use:
solver.parameters.relative_gap_limit = 0.05
For cases where progress stalls or for other reasons, solution callbacks can be used to halt the solver. With these, you can decide on every new solution if the solution is good enough or if the solver should continue searching for a better one. Unlike Gurobi, CP-SAT does not support adding lazy constraints from these callbacks (or at all), which is a significant limitation for problems requiring dynamic model adjustments.
To add a solution callback, inherit from the base class
CpSolverSolutionCallback. Documentation for this base class and its operations
is available
here.
class MySolutionCallback(cp_model.CpSolverSolutionCallback):
def __init__(self, data):
cp_model.CpSolverSolutionCallback.__init__(self)
self.data = data # Store data in the callback.
def on_solution_callback(self):
obj = self.objective_value # Best solution value
bound = self.best_objective_bound # Best bound
print(f"The current value of x is {self.Value(x)}")
if abs(obj - bound) < 10:
self.StopSearch() # Stop search for a better solution
# ...
solver.solve(model, MySolutionCallback(None))
An official example using callbacks is available.
 Bounds in optimization can be a double-edged sword. On one hand, they indicate how close you are to the optimal solution within your chosen model, and they allow you to terminate the optimization process early if the solution is sufficiently close. On the other hand, they can be misleading for two key reasons. First, the bounds pertain to the optimization model and may give a false sense of quality, as neither the model nor the data are typically perfect. Second, in some cases, obtaining good bounds within a reasonable time may be impossible, yet the solution might still be good—you simply may not realize it. This can lead to wasted resources as you pursue tighter models or better approaches with little to no real benefit. While bounds are extremely useful, it is important to understand their origin and limitations, and not regard them as the final determinant of solution quality. |
Besides querying the objective value of the best solution and the best known
bound, you can also access internal metrics such as self.num_booleans,
self.num_branches, and self.num_conflicts. These metrics will be discussed
later.
As of version 9.10, CP-SAT also supports bound callbacks, which are triggered when the proven bound improves. Unlike solution callbacks, which activate upon finding new solutions, bound callbacks are useful for stopping the search when the bound is sufficiently good. The syntax for bound callbacks differs from that of solution callbacks, as they are implemented as free functions that directly access the solver object.
solver = cp_model.CpSolver()
def bound_callback(bound):
print(f"New bound: {bound}")
if bound > 100:
solver.stop_search()
solver.best_bound_callback = bound_callback
Instead of using a simple function, you can also use a callable object to store a reference to the solver object. This approach allows you to define the callback outside the local scope, providing greater flexibility.
class BoundCallback:
def __init__(self, solver) -> None:
self.solver = solver
def __call__(self, bound):
print(f"New bound: {bound}")
if bound > 200:
print("Abort search due to bound")
self.solver.stop_search()
This method is more flexible than the solution callback and can be considered more Pythonic.
Additionally, whenever there is a new solution or bound, a log message is generated. You can hook into the log output to decide when to stop the search using CP-SAT’s log callback.
solver.parameters.log_search_progress = True # Enable logging
solver.log_callback = lambda msg: print("LOG:", msg) # (str) -> None
 Be careful when using callbacks, as they can slow down the solver significantly. Callbacks are often called frequently, forcing a switch back to the slower Python layer. I have often seen students frustrated by slow solver performance, only to discover that most of the solver’s time is spent in the callback function. Even if the operations within the callback are not complex, the time spent can add up quickly and affect overall performance. |
Parallelization
CP-SAT is a portfolio-solver that uses different techniques to solve the problem. There is some information exchange between the different workers, but it does not split the solution space into different parts, thus, it does not parallelize the branch-and-bound algorithm as MIP-solvers do. This can lead to some redundancy in the search, but running different techniques in parallel will also increase the chance of running the right technique. Predicting which technique will be the best for a specific problem is often hard, thus, this parallelization can be quite useful.
By default, CP-SAT leverages all available cores (including hyperthreading). You can control the parallelization of CP-SAT by setting the number of search workers.
solver.parameters.num_workers = 8 # use 8 cores
 For many models, you can boost performance by manually reducing the number of workers to match the number of physical cores, or even fewer. This can be beneficial for several reasons: it allows the remaining workers to run at a higher frequency, provides more memory bandwidth, and reduces potential interference between workers. However, be aware that reducing the number of workers might also decrease the overall chance of one of them making progress, as there are fewer directions being explored simultaneously. |
Here are the solvers used by CP-SAT 9.9 on different parallelization levels for an optimization problem and no additional specifications (e.g., decision strategies). Each row describes the addition of various solvers with respect to the previous row. Note that some parameters/constraints/objectives can change the parallelization strategy. Also check the official documentation.
| # Workers | Full Problem Subsolvers | First Solution Subsolvers | Incomplete Subsolvers | Helper Subsolvers |
|---|---|---|---|---|
| 1 | default_lp | No solver | No solver | No solver |
| 2 | +13 solvers: feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, packing_precedences_lns, packing_rectangles_lns, packing_slice_lns, rins/rens, rnd_cst_lns, rnd_var_lns, scheduling_precedences_lns, violation_ls | +3 solvers: neighborhood_helper, synchronization_agent, update_gap_integral | ||
| 3 | +1 solver: no_lp | |||
| 4 | +1 solver: max_lp | |||
| 5 | +1 solver: fj_short_default | |||
| 6 | +1 solver: quick_restart | |||
| 7 | +1 solver: reduced_costs | |||
| 8 | +1 solver: quick_restart_no_lp | |||
| 12 | +2 solvers: lb_tree_search, pseudo_costs | +2 solvers: fj_long_default, fs_random | ||
| 16 | +3 solvers: objective_lb_search, objective_shaving_search_no_lp, probing | +1 solver: fs_random_quick_restart | ||
| 20 | +2 solvers: objective_shaving_search_max_lp, probing_max_lp | +1 solver: fj_short_lin_default | ||
| 32 | +2 solvers: objective_lb_search_max_lp, objective_lb_search_no_lp | +8 solvers: fj_long_lin_default, fj_long_lin_random, fj_long_random, fj_short_lin_random, fj_short_random, fs_random_no_lp, fs_random_quick_restart_no_lp | +1 solver: violation_ls(3) | |
| 64 | +11 solvers: fj_long_default(2), fj_long_lin_default(2), fj_long_lin_random(2), fj_long_random(2), fj_short_default(2), fj_short_lin_default(2), fj_short_random(2), fs_random(6), fs_random_no_lp(6), fs_random_quick_restart(6), fs_random_quick_restart_no_lp(5) | +1 solver: violation_ls(7) |
Important steps:
- With a single worker, only the default subsolver is used.
- With two workers or more, CP-SAT starts using incomplete subsolvers, i.e., heuristics such as LNS.
- With five workers, CP-SAT will also have a first solution subsolver.
- With 32 workers, all 15 full problem subsolvers are used.
- For more than 32 workers, primarily the number of first solution subsolvers is increased.
Full problem subsolvers are solvers that search the full problem space, e.g., by a branch-and-bound algorithm. Available full problem subsolvers are:
default_lp: LCG-based search with default linearization of the model.max_lp: Same asdefault_lpbut with maximal linearization.no_lp: Same asdefault_lpbut without linearization.
lb_tree_search: This solver is focussed on improving the proven bound, not on finding better solutions. By disproving the feasibility of the cheapest nodes in the search tree, it incrementally improves the bound, but has only little chances to find better solutions.objective_lb_search: Also focussed on improving the bound by disproving the feasibility of the current lower bound.objective_lb_search_max_lp: With maximal linearization.objective_lb_search_no_lp: Without linearization.objective_shaving_search_max_lp: Should be quite similar toobjective_lb_search_max_lp.objective_shaving_search_no_lp: Should be quite similar toobjective_lb_search_no_lp.
probing: Fixing variables and seeing what happens.probing_max_lp: Same as probing but with maximal linearization.
pseudo_costs: Uses pseudo costs for branching, which are computed from historical changes in objective bounds following certain branching decisions.quick_restart: Restarts the search more eagerly. Restarts rebuild the search tree from scratch, but keep learned clauses. This allows to recover from bad decisions, and lead to smaller search trees by learning from the mistakes of the past.quick_restart_no_lp: Same asquick_restartbut without linearization.
reduced_costs: Uses the reduced costs of the linear relaxation for branching.core: A strategy from the SAT-community that extracts unsatisfiable cores of the formula.fixed: User-specified search strategy.
You can modify the used subsolvers by solver.parameters.subsolvers,
solver.parameters.extra_subsolvers, and solver.parameters.ignore_subsolvers.
This can be interesting, e.g., if you are using CP-SAT especially because the
linear relaxation is not useful (and the BnB-algorithm performing badly). There
are even more options, but for these you can simply look into the
documentation.
Be aware that fine-tuning such a solver is not a simple task, and often you do
more harm than good by tinkering around. However, I noticed that decreasing the
number of search workers can actually improve the runtime for some problems.
This indicates that at least selecting the right subsolvers that are best fitted
for your problem can be worth a shot. For example max_lp is probably a waste
of resources if you know that your model has a terrible linear relaxation. In
this context I want to recommend having a look on some relaxed solutions when
dealing with difficult problems to get a better understanding of which parts a
solver may struggle with (use a linear programming solver, like Gurobi, for
this).
You can evaluate the performance of the different strategies by looking at the
Solutions and Objective bounds blocks in the log. Here an example:
Solutions (7) Num Rank
'no_lp': 3 [1,7]
'quick_restart': 1 [3,3]
'quick_restart_no_lp': 3 [2,5]
Objective bounds Num
'initial_domain': 1
'objective_lb_search': 2
'objective_lb_search_no_lp': 4
'objective_shaving_search_no_lp': 1
For solutions, the first number is the number of solutions found by the
strategy, the second number is the range of the ranks of the solutions. The
value [1,7] indicates that the solutions found by the strategy have ranks
between 1 and 7. In this case, it means that the strategy no_lp found the best
and the worst solution.
For objective bounds, the number indicates how often the strategy contributed to
the best bound. For this example, it seems that the no_lp strategies are the
most successful. Note that for both cases, it is more interesting, which
strategies do not appear in the list.
In the search log, you can also see at which time which subsolver contributed something. This log also includes the incomplete and first solution subsolvers.
#1 0.01s best:43 next:[6,42] no_lp (fixed_bools=0/155)
#Bound 0.01s best:43 next:[7,42] objective_shaving_search_no_lp (vars=73 csts=120)
#2 0.01s best:33 next:[7,32] quick_restart_no_lp (fixed_bools=0/143)
#3 0.01s best:31 next:[7,30] quick_restart (fixed_bools=0/123)
#4 0.01s best:17 next:[7,16] quick_restart_no_lp (fixed_bools=2/143)
#5 0.01s best:16 next:[7,15] quick_restart_no_lp (fixed_bools=22/147)
#Bound 0.01s best:16 next:[8,15] objective_lb_search_no_lp
#6 0.01s best:15 next:[8,14] no_lp (fixed_bools=41/164)
#7 0.01s best:14 next:[8,13] no_lp (fixed_bools=42/164)
#Bound 0.01s best:14 next:[9,13] objective_lb_search
#Bound 0.02s best:14 next:[10,13] objective_lb_search_no_lp
#Bound 0.04s best:14 next:[11,13] objective_lb_search_no_lp
#Bound 0.06s best:14 next:[12,13] objective_lb_search
#Bound 0.25s best:14 next:[13,13] objective_lb_search_no_lp
#Model 0.26s var:125/126 constraints:162/162
#Model 2.24s var:124/126 constraints:160/162
#Model 2.58s var:123/126 constraints:158/162
#Model 2.91s var:121/126 constraints:157/162
#Model 2.95s var:120/126 constraints:155/162
#Model 2.97s var:109/126 constraints:140/162
#Model 2.98s var:103/126 constraints:135/162
#Done 2.98s objective_lb_search_no_lp
#Done 2.98s quick_restart_no_lp
#Model 2.98s var:66/126 constraints:91/162
Incomplete subsolvers are solvers that do not search the full problem space,
but work heuristically. Notable strategies are large neighborhood search (LNS)
and feasibility pumps. The first one tries to find a better solution by changing
only a few variables, the second one tries to make infeasible/incomplete
solutions feasible. You can also run only the incomplete subsolvers by setting
solver.parameters.use_lns_only = True, but this needs to be combined with a
time limit, as the incomplete subsolvers do not know when to stop.
First solution subsolvers are strategies that try to find a first solution as fast as possible. They are often used to warm up the solver and to get a first impression of the problem.
If you are interested in how Gurobi parallelizes its search, you can find a great video here. Ed Rothberg also explains the general opportunities and challenges of parallelizing a solver, making it also interesting for understanding the parallelization of CP-SAT.
 This section could need some help as there is the possibility that I am mixing up some of the strategies, or am drawing wrong connections. |
Importing/Exporting Models for Comparison on Different Hardware
If you want to compare the performance of different parallelization levels or different hardware, you can use the following code snippets to export a model. Instead of having to rebuild the model or share any code, you can then simply load the model on a different machine and run the solver.
from ortools.sat.python import cp_model
from ortools.sat import cp_model_pb2
from google.protobuf import text_format
from pathlib import Path
def _detect_binary_mode(filename: str) -> bool:
if filename.endswith((".txt", ".pbtxt", ".pb.txt")):
return False
if filename.endswith((".pb", ".bin", ".proto.bin", ".dat")):
return True
raise ValueError(f"Unknown extension for file: {filename}")
# Changed in ortools 9.15: was model.Proto().SerializeToString() / text_format.MessageToString()
# Now use model.export_to_file() which auto-detects format by extension
def export_model(model: cp_model.CpModel, filename: str, binary: bool | None = None):
binary = _detect_binary_mode(filename) if binary is None else binary
# export_to_file uses .txt extension for text format, otherwise binary
# So we need to handle the mismatch for some extensions
if binary and filename.endswith(".txt"):
# Force binary even with .txt extension - use temp file
temp_file = filename + ".pb"
model.export_to_file(temp_file)
Path(filename).write_bytes(Path(temp_file).read_bytes())
Path(temp_file).unlink()
elif not binary and not filename.endswith(".txt"):
# Force text even without .txt extension
temp_file = filename + ".txt"
model.export_to_file(temp_file)
Path(filename).write_text(Path(temp_file).read_text())
Path(temp_file).unlink()
else:
model.export_to_file(filename)
# Changed in ortools 9.15: was model.Proto().ParseFromString() / text_format.Parse()
# Now use model.Proto().parse_text_format() for text, or cp_model_pb2 for binary
def import_model(filename: str, binary: bool | None = None) -> cp_model.CpModel:
binary = _detect_binary_mode(filename) if binary is None else binary
model = cp_model.CpModel()
if binary:
# Parse binary via standard protobuf, then convert to text for import
proto = cp_model_pb2.CpModelProto()
proto.ParseFromString(Path(filename).read_bytes())
model.Proto().parse_text_format(text_format.MessageToString(proto))
else:
model.Proto().parse_text_format(Path(filename).read_text())
return model
The binary mode is more efficient and should be used for large models. The text mode is human-readable and can be easier shared and compared.
Hints
If you have a good intuition about how the solution might look—perhaps from solving a similar model or using a good heuristic—you can inform CP-SAT to incorporate this knowledge into its search. Some workers will try to follow these hints, which can significantly improve the solver’s performance if they are good. If the hints actually represent a feasible solution, the solver can use them to prune the search space of all branches that have worse bounds than the hints.
model.add_hint(x, 1) # Suggest that x will probably be 1
model.add_hint(y, 2) # Suggest that y will probably be 2
For more examples, refer to the official example. We will also see how to utilize hints for multi-objective optimization in the Coding Patterns chapter.
 Hints can significantly improve solver performance, especially if it struggles to find a good initial solution (as indicated in the logs). This practice is often called warm-starting the solver. You do not need to provide values for all auxiliary variables, but if you use integer variables to approximate continuous variables, it is beneficial to provide hints for these. CP-SAT may struggle with quickly completing the solution, and only completed solutions can be used for pruning the search space. If CP-SAT needs a long time to complete the solution from the hint, it may have wasted a lot of time in branches it could otherwise have pruned. |
To verify that your hints are feasible, you can temporarily fix variables to their hinted values and check if the model becomes infeasible:
solver.parameters.fix_variables_to_their_hinted_value = True
status = solver.solve(model)
if status == cp_model.INFEASIBLE:
print("Hints are conflicting or infeasible!")
If you suspect that your hints are not being utilized, it might indicate a logical error in your model or a bug in your code. This approach reliably detects infeasible hints by forcing the solver to use the exact hinted values.
There is also solver.parameters.debug_crash_on_bad_hint = True, which crashes
the solver if it cannot complete hints into a feasible solution. However, this
feature is unreliable: it only triggers in multi-worker mode, depends on a race
condition between workers, and is controlled by hint_conflict_limit (default:
10). The fix_variables_to_their_hinted_value approach above is simpler and
deterministic.
 In older versions of CP-SAT, hints could sometimes visibly slow down the solver, even if they were correct but not optimal. While this issue seems resolved in the latest versions, it is important to note that bad hints can still cause slowdowns by guiding the solver in the wrong direction. |
Often, you may need to explore the impact of forcing certain variables to specific values. To avoid copying the entire model multiple times to set the values of variables explicitly, you can also use hints to fix variables their hinted value with the following parameter:
solver.parameters.fix_variables_to_their_hinted_value = True
Hints can be cleared afterwards by calling model.clear_hints(), allowing you
to test other hints without duplicating the model. While you cannot add complex
expressions directly, fixing variables enables you to experiment with more
intricate constraints without model duplication. For temporary complex
constraints, model copying using model.CopyFrom may still be necessary, along
with variable copying.
You can also use this function to complete hints for auxiliary variables, which are often tedious and error-prone to set manually. To do so, invoke the function below before solving the model. Adjust the time limit based on the difficulty of completing the hint. If the values can be determined through simple propagation, even large models can be processed quickly.
def complete_hint(
model: cp_model.CpModel,
time_limit: float = 0.5,
):
"""
Completes the hint via a limited solve. Since CP-SAT only accepts complete hints,
performing this step can improve solver performance.
Args:
model: The CpModel object to update.
time_limit: Time limit for the solve (in seconds).
Notes:
This function performs a quick solve to deduce variable values.
If successful, it replaces any existing hint with a complete one.
If not successful, the model remains unchanged and a warning is issued.
"""
logging.info("Completing hint with a time limit of %d seconds", time_limit)
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit
solver.parameters.fix_variables_to_their_hinted_value = True
status = solver.solve(model)
logging.info(
"Automatically completing hint with status: %s", solver.status_name(status)
)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
# Clear the existing hint to avoid model invalidation.
model.clear_hints()
# Set a new complete hint using the solver result.
for i, _ in enumerate(model.proto.variables):
v_ = model.get_int_var_from_proto_index(i)
model.add_hint(v_, solver.value(v_))
logging.info(
"Hint successfully completed within time limit. Status: %s",
solver.status_name(status),
)
else:
logging.warning(
"Unable to complete hint within time limit. Status: %s",
solver.status_name(status),
)
 During presolve, the model is modified. For example, symmetries may be broken by prohibiting equivalent variations of the same solution. While such modifications can significantly improve performance by reducing the search space, they make it difficult to maintain the feasibility of hints, e.g., if a hint corresponds to a pruned variation. Unfortunately, CP-SAT has historically struggled to preserve the feasibility of hints through presolve. Although some issues have been resolved in earlier versions, I am still encountering this behavior in recent releases. As a workaround, you can instruct CP-SAT to retain all feasible solutions during presolve by setting: However, enabling this parameter may degrade solver performance. If you observe that hints become infeasible after presolve, you should experimentally determine whether maintaining feasible hints or doing the full presolve is more beneficial. |
Reinforcing the Model
For advanced users working with CP-SAT incrementally—i.e., modifying and solving the model multiple times—the following parameter may be of interest:
solver.parameters.fill_tightened_domains_in_response = True
When you remove the objective function and solve the feasibility version of your model, the solver returns tightened domains for the variables. This can significantly reduce the search space, improving solver performance, especially when solving the model multiple times with different objectives or additional constraints.
However, if the objective function is left in place, feasible solutions may be excluded from the search space. These solutions might become relevant if the objective or constraints are altered later.
Enabling this parameter does not modify the model itself; rather, it provides a list of tightened variable domains in the response object which you can then use in your model.
# Example after solving the model
for i, v in enumerate(self.model.proto.variables):
print(f"Tightened domain for variable {i} '{v.name}' is {solver.response_proto.tightened_variables[i].domain}")
Assumptions
Another way to explore the impact of forcing certain variables to specific values is by means of assumptions, which is a common feature in many SAT solvers. Unlike fixing hinted values, assumptions are restricted to boolean literals in CP-SAT.
b1 = model.new_bool_var("b1")
b2 = model.new_bool_var("b2")
b3 = model.new_bool_var("b3")
model.add_assumptions([b1, ~b2]) # assume b1=True, b2=False
model.add_assumption(b3) # assume b3=True (single literal)
# ... solve again and analyze ...
model.clear_assumptions() # clear all assumptions
 While incremental SAT solvers can reuse learned clauses from previous runs despite changes in assumptions, CP-SAT does not support this feature. Its solver is stateless and always starts from scratch. |
While assumptions can be used to explore different assignments of Boolean
variables without reconstructing the model, CP-SAT offers a more powerful
feature: the extraction of unsatisfiable cores from infeasible models. This
capability is particularly useful for model debugging. By enabling constraints
conditionally using only_enforce_if(b) and adding b as an assumption, one
can isolate sources of infeasibility. If the model proves infeasible, CP-SAT can
return a minimal subset of the assumptions, and thus the corresponding
constraints, that lead to the conflict.
Consider the following example. Suppose we have a model with three integer variables \( x \), \( y \), and \( z \), along with the following constraints:
- \( x + y \leq 4 \)
- \( x + z \leq 2 \)
- \( z \geq 4 \)
Since all variables are non-negative integers, this model is clearly infeasible
due to the incompatibility between constraints (2) and (3). When dealing with
larger models, identifying the source of infeasibility can be challenging.
However, by using assumptions in conjunction with
sufficient_assumptions_for_infeasibility, CP-SAT can automatically identify
which constraints are responsible.
from ortools.sat.python import cp_model
model = cp_model.CpModel()
# Integer variables
x = model.new_int_var(0, 100, 'x')
y = model.new_int_var(0, 100, 'y')
z = model.new_int_var(0, 100, 'z')
# Constraints
indicator_1 = model.new_bool_var('Indicator 1: x + y <= 4')
model.add(x + y <= 4).only_enforce_if(indicator_1)
indicator_2 = model.new_bool_var('Indicator 2: x + z <= 2')
model.add(x + z <= 2).only_enforce_if(indicator_2)
indicator_3 = model.new_bool_var('Indicator 3: z >= 4')
model.add(z >= 4).only_enforce_if(indicator_3)
# Assumptions
model.add_assumptions([indicator_1, indicator_2, indicator_3])
# Solve
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.INFEASIBLE
print("Minimal unsat core:")
for var_index in solver.sufficient_assumptions_for_infeasibility():
print(f"{var_index}: '{model.proto.variables[var_index].name}'")
This produces the following output:
Minimal unsat core:
4: 'Indicator 2: x + z <= 2'
5: 'Indicator 3: z >= 4'
Unfortunately, not all constraints in CP-SAT support reification. However, lower-level constraints, where infeasibilities are most likely to occur, typically do. For higher-level constraints, workarounds may exist to express them in a reifiable form.
 You can find more information on this in the CPMpy documentation, a modelling library that also supports CP-SAT as backend. |
Presolve
The CP-SAT solver includes a presolve step that simplifies the model before solving it. This step can significantly reduce the search space and enhance performance. However, presolve can be time-consuming, particularly for large models. If your model is relatively simple—meaning there are few genuinely challenging decisions for CP-SAT to make—and you notice that presolve is taking a long time while the search itself is fast, you might consider reducing the presolve effort.
For example, you can disable presolve entirely with:
solver.parameters.cp_model_presolve = False
However, this approach might be too drastic, so you may prefer to limit presolve rather than disabling it completely.
To reduce the number of presolve iterations, you can use:
solver.parameters.max_presolve_iterations = 3
You can also limit specific presolve techniques. For instance, you can constrain the time or intensity of probing, which is a technique that tries to fix variables and observe the outcome. Although probing can be powerful, it is also time-intensive.
solver.parameters.cp_model_probing_level = 1
solver.parameters.presolve_probing_deterministic_time_limit = 5
There are additional parameters available to control presolve. Before making adjustments, I recommend reviewing the solver log to identify which aspects of presolve are causing long runtimes.
Keep in mind that reducing presolve increases the risk of failing to solve more complex models. Ensure that you are not sacrificing performance on more challenging instances just to speed up simpler cases.
Adding Your Own Subsolver to the Portfolio
As we have seen, CP-SAT uses a portfolio of different subsolvers, each configured with varying settings (e.g., different levels of linearization) to solve the model. You can also define your own subsolver with a specific configuration. It is important not to modify the parameters at the top level, as this would affect all subsolvers, including the LNS-workers. Doing so could disrupt the balance of the portfolio, potentially activating costly techniques for the LNS-workers, which could slow them down to the point of being ineffective. Additionally, you risk creating a default subsolver incompatible with your model - such as one that requires an objective function - causing CP-SAT to exclude most or all subsolvers from the portfolio, resulting in a solver that is either inefficient or nonfunctional.
For example, in packing problems, certain expensive propagation techniques can significantly speed up the search but can also drastically slow it down if misused. To handle this, you can add a single subsolver that applies these techniques. If the parameters do not help, only one worker will be slowed down, while the rest of the portfolio remains unaffected. However, if the parameters are beneficial, that worker can share its solutions and (variable) bounds with the rest of the portfolio, boosting overall performance.
Here is how you can define and add a custom subsolver:
from ortools.sat import sat_parameters_pb2
packing_subsolver = sat_parameters_pb2.SatParameters()
packing_subsolver.name = "MyPackingSubsolver"
packing_subsolver.use_area_energetic_reasoning_in_no_overlap_2d = True
packing_subsolver.use_energetic_reasoning_in_no_overlap_2d = True
packing_subsolver.use_timetabling_in_no_overlap_2d = True
packing_subsolver.max_pairs_pairwise_reasoning_in_no_overlap_2d = 5_000
# Add the subsolver to the portfolio
solver.parameters.subsolver_params.append(packing_subsolver) # Define the subsolver
solver.parameters.extra_subsolvers.append(
packing_subsolver.name
) # Activate the subsolver
After adding the subsolver, you can check the log to verify that it is included in the list of active subsolvers. If it is not shown, you probably used parameters incompatible with the model, causing the subsolver to be excluded.
8 full problem subsolvers: [MyPackingSubsolver, default_lp, max_lp, no_lp, probing, probing_max_lp, quick_restart, quick_restart_no_lp]
If you want to find out how the existing subsolvers are configured, you can check out the cp_model_search.cc file in the OR-Tools repository.
 You can also overwrite the parameters of an existing subsolver by using the same name. Only the parameters you explicitly change will be updated, while the others will remain as they are. Additionally, you can add multiple subsolvers to the portfolio, but keep in mind that doing so might push some predefined subsolvers out of the portfolio if there are not enough workers available. |
Decision Strategy
In the end of this section, a more advanced parameter that looks interesting for
advanced users as it gives some insights into the search algorithm. It can be
useful in combination with solver.parameters.enumerate_all_solutions = True to
specify the order in which all solutions are iterated. It can also have some
impact on the search performance for normal optimization, but this is often hard
to predict, thus, you should leave the following parameters unless you have a
good reason to change them.
We can tell CP-SAT, how to branch (or make a decision) whenever it can no longer deduce anything via propagation. For this, we need to provide a list of the variables (order may be important for some strategies), define which variable should be selected next (fixed variables are automatically skipped), and define which value should be probed.
We have the following options for variable selection:
CHOOSE_FIRST: the first not-fixed variable in the list.CHOOSE_LOWEST_MIN: the variable that could (potentially) take the lowest value.CHOOSE_HIGHEST_MAX: the variable that could (potentially) take the highest value.CHOOSE_MIN_DOMAIN_SIZE: the variable that has the fewest feasible assignments.CHOOSE_MAX_DOMAIN_SIZE: the variable the has the most feasible assignments.
For the value/domain strategy, we have the options:
SELECT_MIN_VALUE: try to assign the smallest value.SELECT_MAX_VALUE: try to assign the largest value.SELECT_LOWER_HALF: branch to the lower half.SELECT_UPPER_HALF: branch to the upper half.SELECT_MEDIAN_VALUE: try to assign the median value.
model.add_decision_strategy([x], cp_model.CHOOSE_FIRST, cp_model.SELECT_MIN_VALUE)
# your can force CP-SAT to follow this strategy exactly
solver.parameters.search_branching = cp_model.FIXED_SEARCH
For example for coloring (with
integer representation of the color), we could order the variables by decreasing
neighborhood size (CHOOSE_FIRST) and then always try to assign the lowest
color (SELECT_MIN_VALUE). This strategy should perform an implicit
kernelization, because if we need at least \( k \) colors, the vertices with less
than \( k \) neighbors are trivial (and they would not be relevant for any
conflict). Thus, by putting them at the end of the list, CP-SAT will only
consider them once the vertices with higher degree could be colored without any
conflict (and then the vertices with lower degree will, too). Another strategy
may be to use CHOOSE_LOWEST_MIN to always select the vertex that has the
lowest color available. Whether this will actually help, has to be evaluated:
CP-SAT will probably notice by itself which vertices are the critical ones after
some conflicts.
 I played around a little with selecting a manual search strategy. But even for the coloring, where this may even seem smart, it only gave an advantage for a bad model and after improving the model by symmetry breaking, it performed worse. Further, I assume that CP-SAT can learn the best strategy (Gurobi does such a thing, too) much better dynamically on its own. |
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Understanding the Log
Understanding the CP-SAT Log

If you want to master CP-SAT, understanding the log is crucial. The log is the output of the solver that shows you what the solver is doing and how it is progressing.
The log consists of different parts. Let us go through them step by step.
 Use the Log Analyzer to get your
own logs explained to you.
|
As a reminder, you activate logging with
solver.parameters.log_search_progress = True # Enable logging
Initialization
The log starts with the version of CP-SAT, the parameters you set, and how many
workers it has been using. For example, we have set a time limit via
max_time_in_seconds to 30 seconds. If you are given a log, you can directly
see under which conditions the solver was running.
Starting CP-SAT solver v9.10.4067
Parameters: max_time_in_seconds: 30 log_search_progress: true relative_gap_limit: 0.01
Setting number of workers to 16
Initial Model Description
The next block provides an overview of the model before presolve, detailing the number of variables and constraints, as well as their coefficients and domains.
Initial optimization model '': (model_fingerprint: 0x1d316fc2ae4c02b1)
#Variables: 450 (#bools: 276 #ints: 6 in objective)
- 342 Booleans in [0,1]
- 12 in [0][10][20][30][40][50][60][70][80][90][100]
- 6 in [0][10][20][30][40][100]
- 6 in [0][80][100]
- 6 in [0][100]
- 6 in [0,1][34][67][100]
- 12 in [0,6]
- 18 in [0,7]
- 6 in [0,35]
- 6 in [0,36]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kBoolOr: 30 (#literals: 72)
#kLinear1: 33 (#enforced: 12)
#kLinear2: 1'811
#kLinear3: 36
#kLinearN: 94 (#terms: 1'392)
For example, - 12 in [22,57] indicates that there are 12 variables with a
domain of [22,57], meaning their values can range between 22 and 57.
Similarly, #kLinearN: 94 (#terms: 1'392) indicates the presence of 94 linear
constraints with 1,392 coefficients.
Comparing this data to the model after presolve (coming up soon) is useful to ensure it aligns with your expectations. The presolve phase often reformulates your model extensively to enhance efficiency.
Since most optimization models are created dynamically in code, reviewing this section can help identify bugs or inefficiencies. Take the time to verify that the numbers match your expectations and ensure you do not have too many or too few variables or constraints of a certain type. This step is crucial as it also provides insight into the number of auxiliary variables in your model, helping you better understand its structure and complexity.
Presolve Log
The next block represents the presolve phase, an essential component of CP-SAT.
During this phase, the solver reformulates your model for greater efficiency.
For instance, it may detect an affine relationship between variables, such as
x=2y-1, and replace x with 2y-1 in all constraints. It can also identify
and remove redundant constraints or unnecessary variables. For example, the log
entry rule 'presolve: 33 unused variables removed.' was applied 1 time may
indicate that some variables created by your code were unnecessary or became
redundant due to the reformulation. Multiple rounds of applying various rules
for domain reduction, expansion, equivalence checking, substitution, and probing
are performed during presolve. These rules can significantly enhance the
efficiency of your model, though they may take some time to run. However, this
time investment usually pays off during the search phase.
Starting presolve at 0.00s
3.26e-04s 0.00e+00d [DetectDominanceRelations]
6.60e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=4 #num_dual_strengthening=3
2.69e-05s 0.00e+00d [ExtractEncodingFromLinear] #potential_supersets=44 #potential_subsets=12
[Symmetry] Graph for symmetry has 2'224 nodes and 5'046 arcs.
[Symmetry] Symmetry computation done. time: 0.000374304 dtime: 0.00068988
[Symmetry] #generators: 2, average support size: 12
[Symmetry] 12 orbits with sizes: 2,2,2,2,2,2,2,2,2,2,...
[Symmetry] Found orbitope of size 6 x 2
[SAT presolve] num removable Booleans: 0 / 309
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [3.0778e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [4.6758e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
1.10e-02s 9.68e-03d [Probe] #probed=1'738 #new_bounds=12 #new_binary_clauses=1'111
2.34e-03s 0.00e+00d [MaxClique] Merged 602(1374 literals) into 506(1960 literals) at_most_ones.
3.31e-04s 0.00e+00d [DetectDominanceRelations]
1.89e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=1
5.45e-04s 0.00e+00d [ProcessAtMostOneAndLinear]
8.19e-04s 0.00e+00d [DetectDuplicateConstraints] #without_enforcements=306
8.62e-05s 7.21e-06d [DetectDominatedLinearConstraints] #relevant_constraints=114 #num_inclusions=42
...
Presolve summary:
- 54 affine relations were detected.
- rule 'TODO dual: make linear1 equiv' was applied 6 times.
- rule 'TODO dual: only one blocking constraint?' was applied 1'074 times.
- rule 'TODO dual: only one unspecified blocking constraint?' was applied 48 times.
- rule 'TODO duplicate: identical constraint with different enforcements' was applied 612 times.
- rule 'TODO linear2: contains a Boolean.' was applied 1'626 times.
- rule 'TODO symmetry: add symmetry breaking inequalities?' was applied 2 times.
...
- rule 'objective: variable not used elsewhere' was applied 15 times.
- rule 'presolve: 33 unused variables removed.' was applied 1 time.
- rule 'presolve: iteration' was applied 2 times.
- rule 'variables with 2 values: create encoding literal' was applied 12 times.
- rule 'variables with 2 values: new affine relation' was applied 12 times.
- rule 'variables: canonicalize affine domain' was applied 30 times.
- rule 'variables: detect half reified value encoding' was applied 54 times.
The presolve log can be challenging to read, but it provides vital information on the simplifications and optimizations made by CP-SAT. Reviewing this log can help you understand the transformations applied to your model, allowing you to identify and address any unnecessary variables or constraints in your code.
Presolved Model
This is the most important block of the presolve phase and gives an overview of the model after presolve. It contains the number of variables and constraints, as well as coefficients and domains.
- 200 in [0,199] will indicate that there are 200 variables with domain
[0,199], i.e., values between 0 and 199. - 6 in [0,1][34][67][100] will
indicate that there are 6 variables with domain [0,1][34][67][100], i.e.,
values 0, 1, 34, 67, and 100. #kLinearN: 3'000 (#terms: 980'948) indicates
that there are 3000 linear constraints with 980’948 coefficients.
It is useful to compare this to the initial model, to see if your model was simplified by presolve, which indicates that you can simplify your model yourself, saving presolve time. If you notice that a lot of time is spent in presolve but it does not simplify your model, you can try to disable/reduce presolve.
It is also interesting to see if the presolve replaced some of your constraints with more efficient ones.
Presolved optimization model '': (model_fingerprint: 0xb4e599720afb8c14)
#Variables: 405 (#bools: 261 #ints: 6 in objective)
- 309 Booleans in [0,1]
- 12 in [0][2,6]
- 6 in [0][4,5]
- 6 in [0,3]
- 6 in [0,4]
- 6 in [0,6]
- 6 in [0,7]
- 12 in [0,10]
- 12 in [0,13]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kAtMostOne: 452 (#literals: 1'750)
#kBoolAnd: 36 (#enforced: 36) (#literals: 90)
#kBoolOr: 12 (#literals: 36)
#kLinear1: 854 (#enforced: 854)
#kLinear2: 42
#kLinear3: 24
#kLinearN: 48 (#enforced: 18) (#terms: 1'046)
 This is the same model as in the initial model description. Take some time to compare the two and see how much the presolve-phase has reformulated the model. |
Preloading Model
This block serves as a prelude to the search phase and provides an overview of the model at the beginning of the search. Typically, this information is not very interesting unless the presolve phase was highly effective, essentially solving the model before the search phase begins. This can lead to entries that look very similar to that of the actual search phase, which comes next.
Preloading model.
#Bound 0.05s best:-inf next:[-0.7125] initial_domain
[Symmetry] Graph for symmetry has 2,111 nodes and 5,096 arcs.
[Symmetry] Symmetry computation done. time: 0.000365377 dtime: 0.00068122
[Symmetry] #generators: 2, average support size: 12
[Symmetry] Found orbitope of size 6 x 2
#Model 0.05s var:405/405 constraints:1468/1468
Search Phase
The search progress log is an essential element of the overall log, crucial for identifying performance bottlenecks. It clearly demonstrates the solver’s progression over time and pinpoints where it faces significant challenges. It is important to discern whether the upper or lower bounds are causing issues, or if the solver initially finds a near-optimal solution but struggles to minimize a small remaining gap.
 For models without an objective, especially the log of the search phase will look very different. This chapter focuses on models with an objective. |
The structure of the log entries is standardized as follows:
EVENT NAME | TIME | BEST SOLUTION | RANGE OF THE SEARCH | COMMENT
For instance, an event marked #2 indicates the discovery of the second
solution. Here, you will observe an improvement in the BEST SOLUTION metric. A
notation like best:16 confirms that the solver has found a solution with a
value of 16.
An event with #Bound denotes an enhancement in the bound, as seen by a
reduction in the RANGE OF THE SEARCH. A detail such as next:[7,14] signifies
that the solver is now focused on finding a solution valued between 7 and 14.
The COMMENT section provides essential information about the strategies that
led to these improvements.
Events labeled #Model signal modifications to the model, such as fixing
certain variables.
Starting search at 0.05s with 16 workers.
11 full problem subsolvers: [core, default_lp, lb_tree_search, max_lp, no_lp, objective_lb_search, probing, pseudo_costs, quick_restart, quick_restart_no_lp, reduced_costs]
4 first solution subsolvers: [fj_long_default, fj_short_default, fs_random, fs_random_quick_restart]
9 incomplete subsolvers: [feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, rins/rens, rnd_cst_lns, rnd_var_lns, violation_ls]
3 helper subsolvers: [neighborhood_helper, synchronization_agent, update_gap_integral]
#1 0.06s best:-0 next:[1,7125] fj_short_default(batch:1 #lin_moves:0 #lin_evals:0 #weight_updates:0)
#2 0.07s best:1050 next:[1051,7125] fj_long_default(batch:1 #lin_moves:1'471 #lin_evals:2'102 #weight_updates:123)
#3 0.08s best:1051 next:[1052,7125] quick_restart_no_lp (fixed_bools=0/884)
#Bound 0.09s best:1051 next:[1052,1650] default_lp
#4 0.10s best:1052 next:[1053,1650] quick_restart_no_lp (fixed_bools=22/898)
#5 0.10s best:1053 next:[1054,1650] quick_restart_no_lp (fixed_bools=22/901)
#6 0.11s best:1055 next:[1056,1650] quick_restart_no_lp (fixed_bools=22/906)
#7 0.11s best:1056 next:[1057,1650] quick_restart_no_lp (fixed_bools=22/909)
#8 0.11s best:1057 next:[1058,1650] quick_restart_no_lp (fixed_bools=22/913)
#9 0.11s best:1058 next:[1059,1650] quick_restart_no_lp (fixed_bools=22/914)
#10 0.12s best:1059 next:[1060,1650] quick_restart_no_lp (fixed_bools=26/916)
#11 0.12s best:1060 next:[1061,1650] quick_restart_no_lp (fixed_bools=26/917)
#12 0.12s best:1061 next:[1062,1650] quick_restart_no_lp (fixed_bools=26/918)
#13 0.13s best:1062 next:[1063,1650] quick_restart_no_lp (fixed_bools=28/918)
#14 0.13s best:1063 next:[1064,1650] quick_restart_no_lp (fixed_bools=28/921)
#Bound 0.13s best:1063 next:[1064,1579] lb_tree_search
#15 0.13s best:1064 next:[1065,1579] quick_restart_no_lp (fixed_bools=28/924)
#Model 0.13s var:404/405 constraints:1435/1468
#16 0.13s best:1065 next:[1066,1579] quick_restart_no_lp (fixed_bools=28/930)
#17 0.13s best:1066 next:[1067,1579] quick_restart_no_lp (fixed_bools=28/932)
#18 0.14s best:1067 next:[1068,1579] quick_restart_no_lp (fixed_bools=28/935)
#19 0.14s best:1071 next:[1072,1579] quick_restart_no_lp (fixed_bools=28/946)
#20 0.15s best:1072 next:[1073,1579] quick_restart_no_lp (fixed_bools=28/950)
#21 0.15s best:1089 next:[1090,1579] quick_restart_no_lp (fixed_bools=28/966)
#22 0.15s best:1090 next:[1091,1579] quick_restart_no_lp (fixed_bools=28/966)
...
#Bound 8.73s best:1449 next:[1450,1528] lb_tree_search (nodes=13/18 rc=0 decisions=133 @root=28 restarts=0)
#Model 8.99s var:390/405 constraints:1292/1468
#Bound 9.37s best:1449 next:[1450,1527] lb_tree_search (nodes=15/20 rc=0 decisions=152 @root=28 restarts=0)
#Bound 11.79s best:1449 next:[1450,1526] lb_tree_search (nodes=78/83 rc=0 decisions=327 @root=28 restarts=0)
#Bound 12.40s best:1449 next:[1450,1525] lb_tree_search (nodes=96/104 rc=0 decisions=445 @root=28 restarts=0)
#Bound 13.50s best:1449 next:[1450,1524] lb_tree_search (nodes=123/138 rc=0 decisions=624 @root=28 restarts=0)
#Bound 15.71s best:1449 next:[1450,1523] lb_tree_search (nodes=164/180 rc=0 decisions=847 @root=29 restarts=0)
#132 16.69s best:1450 next:[1451,1523] rnd_var_lns (d=0.88 s=657 t=0.10 p=0.54 stall=53 h=folio_rnd)
#Bound 17.13s best:1450 next:[1451,1522] lb_tree_search (nodes=176/192 rc=0 decisions=1001 @root=30 restarts=0)
#Model 17.85s var:389/405 constraints:1289/1468
#Bound 19.35s best:1450 next:[1451,1521] lb_tree_search (nodes=44/44 rc=0 decisions=1112 @root=33 restarts=1)
#Bound 20.12s best:1450 next:[1451,1520] lb_tree_search (nodes=53/53 rc=0 decisions=1176 @root=34 restarts=1)
#Bound 22.08s best:1450 next:[1451,1519] lb_tree_search (nodes=114/114 rc=0 decisions=1369 @root=35 restarts=1)
#Bound 23.92s best:1450 next:[1451,1518] lb_tree_search (nodes=131/131 rc=0 decisions=1517 @root=36 restarts=1)
#Bound 25.84s best:1450 next:[1451,1517] lb_tree_search (nodes=174/174 rc=0 decisions=1754 @root=36 restarts=1)
#Bound 29.35s best:1450 next:[1451,1515] objective_lb_search
As this log is event-driven, it can be challenging to interpret. The Log Analyzer helps by automatically plotting these values in a more understandable way. Since the values at the beginning of the search are often out of scale, use the zoom function to focus on the relevant parts of the search.
 | 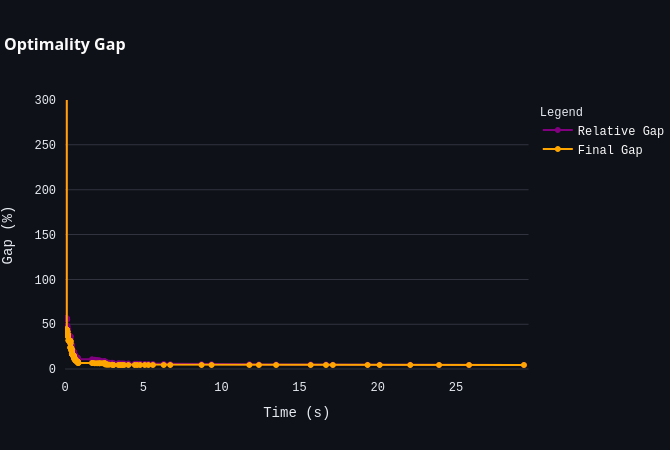 |  |
|---|---|---|
| Shows how the lower and upper bounds change over time. | Shows how quickly the optimality gap converges. | Shows how the model changes over time as new insights from the search allow the solver to fix variables. |
Subsolver Details
Now there comes a lot of information about the different subsolvers that are used. This is a very detailed part of the log and can be overwhelming. You already need to be rather deep into the details of CP-SAT to actually make any use of this information. It is primarily intended for the developers of CP-SAT. It gives you insights into how the various subsolvers have been contributing to the solution, how the otherwise hidden LP-techniques, including cutting planes, have been used, and how the different heuristics have been applied. Based on this data, you could try to tune the various parameters of CP-SAT for your problem. However, note that you will probably need a lot of experience and experiments to gain an advantage compared to the default settings.
Task timing n [ min, max] avg dev time n [ min, max] avg dev dtime
'core': 1 [ 29.95s, 29.95s] 29.95s 0.00ns 29.95s 1 [ 27.99s, 27.99s] 27.99s 0.00ns 27.99s
'default_lp': 1 [ 29.94s, 29.94s] 29.94s 0.00ns 29.94s 1 [ 21.11s, 21.11s] 21.11s 0.00ns 21.11s
'feasibility_pump': 123 [ 4.51ms, 70.61ms] 38.93ms 9.87ms 4.79s 122 [ 6.31ms, 41.77ms] 17.96ms 6.53ms 2.19s
'fj_long_default': 1 [ 10.28ms, 10.28ms] 10.28ms 0.00ns 10.28ms 1 [ 2.08ms, 2.08ms] 2.08ms 0.00ns 2.08ms
'fj_short_default': 1 [579.83us, 579.83us] 579.83us 0.00ns 579.83us 0 [ 0.00ns, 0.00ns] 0.00ns 0.00ns 0.00ns
'fs_random': 1 [ 6.57ms, 6.57ms] 6.57ms 0.00ns 6.57ms 1 [ 20.00ns, 20.00ns] 20.00ns 0.00ns 20.00ns
'fs_random_quick_restart': 1 [ 6.82ms, 6.82ms] 6.82ms 0.00ns 6.82ms 1 [ 20.00ns, 20.00ns] 20.00ns 0.00ns 20.00ns
'graph_arc_lns': 123 [ 3.65ms, 430.55ms] 169.44ms 106.16ms 20.84s 123 [ 10.00ns, 119.31ms] 61.95ms 43.70ms 7.62s
...
Clauses shared Num
'core': 137
'default_lp': 1
'lb_tree_search': 4
'max_lp': 1
'no_lp': 10
'objective_lb_search': 3
'pseudo_costs': 4
'quick_restart': 4
'quick_restart_no_lp': 74
'reduced_costs': 2
Summary
This final block of the log contains a summary by the solver. Here you find the most important information, such as how successful the search was.
You can find the original documentation here.
CpSolverResponse summary:
status: FEASIBLE # The status of the search. Can be FEASIBLE, OPTIMAL, INFEASIBLE, UNKNOWN, or MODEL_INVALID.
objective: 1450 # The value of the objective function for the best solution found.
best_bound: 1515 # The proven bound on the objective function, i.e., the best possible value.
integers: 416
booleans: 857
conflicts: 0
branches: 370
propagations: 13193
integer_propagations: 6897
restarts: 370
lp_iterations: 0
walltime: 30.4515 # The time in seconds since solver creation.
usertime: 30.4515
deterministic_time: 306.548
gap_integral: 1292.47 # The integral of the gap over time. A lower value will indicate that the solver is converging faster.
solution_fingerprint: 0xf10c47f1901c2c16 # Useful to check if two runs result in the same solution.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
How does it work?
How does it work?

CP-SAT is a versatile portfolio solver, centered around a Lazy Clause Generation (LCG) based Constraint Programming Solver, although it encompasses a broader spectrum of technologies.
In its role as a portfolio solver, CP-SAT concurrently executes a multitude of diverse algorithms and strategies, each possessing unique strengths and weaknesses. These elements operate largely independently but engage in information exchange, sharing progress when better solutions emerge or tighter bounds become available.
While this may initially appear as an inefficient approach due to potential redundancy, it proves highly effective in practice. The rationale behind this lies in the inherent challenge of predicting which algorithm is best suited to solve a given problem (No Free Lunch Theorem). Thus, the pragmatic strategy involves running various approaches in parallel, with the hope that one will effectively address the problem at hand. Note that you can also specify which algorithms should be used if you already know which strategies are promising or futile.
In contrast, Branch and Cut-based Mixed Integer Programming solvers like Gurobi implement a more efficient partitioning of the search space to reduce redundancy. However, they specialize in a particular strategy, which may not always be the optimal choice, although it frequently proves to be so.
CP-SAT employs Branch and Cut techniques, including linear relaxations and cutting planes, as part of its toolkit. Models that can be efficiently addressed by a Mixed Integer Programming (MIP) solver are typically a good match for CP-SAT as well. Nevertheless, CP-SAT’s central focus is the implementation of Lazy Clause Generation, harnessing SAT-solvers rather than relying primarily on linear relaxations. As a result, CP-SAT may exhibit somewhat reduced performance when confronted with MIP problems compared to dedicated MIP solvers. However, it gains a distinct advantage when dealing with problems laden with intricate logical constraints.
The concept behind Lazy Clause Generation involves the (incremental) transformation of the problem into a SAT-formula, subsequently employing a SAT-solver to seek a solution (or prove bounds by infeasibility). To mitigate the impracticality of a straightforward conversion, Lazy Clause Generation leverages an abundance of lazy variables and clauses.
Notably, the Cook-Levin Theorem attests that any problem within the realm of NP can be translated into a SAT-formula. Optimization, in theory, could be achieved through a simple binary search. However, this approach, while theoretically sound, lacks efficiency. CP-SAT employs a more refined encoding scheme to tackle optimization problems more effectively.
If you want to understand the inner workings of CP-SAT, you can follow the following learning path:
- Learn how to get a feasible solution based on boolean logics with SAT-solvers: Backtracking, DPLL, CDCL, VSIDS, …
- Learn how to get provably optimal solutions via classical Mixed Integer
Programming:
- Linear Programming: Simplex, Duality, Dual Simplex, …
- Understanding and Using Linear Programming (book)
- Optimization in Operations Research by Ronald Rardin (very long book also containing Mixed Integer Programming, Heuristics, and advanced topics. For those who want to dive deep.)
- Video Series by Gurobi
- Mixed Integer Programming: Branch and Bound, Cutting Planes, Branch and
Cut, …
- Gurobi Resources (website)
- Linear Programming: Simplex, Duality, Dual Simplex, …
- Learn the additional concepts of LCG Constraint Programming: Propagation, Lazy Clause Generation, …
- Learn the details of CP-SAT:
- The proto-file of the parameters (source)
- The complete source code (source)
- A recent talk by the developers of CP-SAT (video)
- Another recent talk by the developers of CP-SAT (video)
- A talk by the developers of CP-SAT (video)
If you already have a background in Mixed Integer Programming, you may directly jump into the slides of Combinatorial Optimisation and Constraint Programming. This is a full and detailed course on constraint programming, and will probably take you some time to work through. However, it gives you all the knowledge you need to understand the constraint programming part of CP-SAT.
Originally, I wrote a short introduction into each of the topics, but I decided to remove them as the material I linked to is much better than what I could have written. You can find a backup of the old version here.
What Happens in CP-SAT During Solve?
What exactly happens when you run solver.solve(model)?
-
Model Loading and Verification:
- The model is read from its protobuf representation.
- The model is verified for correctness.
-
Preprocessing (multiple iterations, controlled by
max_presolve_iterations):- Presolve (domain reduction):
- This step reduces the problem size by simplifying variable domains. For more on this, check out:
- Expansion of higher-level constraints:
- Higher-level constraints are expanded into lower-level constraints, CP-SAT actually can propagate efficiently, but which are less comfortable for you to write. See FlatZinc and Flattening for a similar process.
- Detection of equivalent variables and affine relations:
- Affine relations, such as
a * x + b = y, are identified. Read more about affine relations here.
- Affine relations, such as
- Substitution with canonical representations:
- Detected affine relations are replaced with canonical representations.
- Variable probing:
- Some variables are tested to determine if they can be fixed or if further equivalences can be identified.
- Presolve (domain reduction):
-
Loading and Relaxation:
- The preprocessed model is loaded into the underlying solver, and linear relaxations are created.
-
Solution Search:
- The solver searches for solutions and bounds until the lower and upper bounds converge or another stopping criterion is met (e.g., time limit).
- Several full subsolvers, each using a unique strategy, are run across
different threads. These strategies may include:
- More linearized models
- Aggressive restarts
- Focus on either the lower or upper bound
- Each subsolver can theoretically find the optimal solution, but some are faster than others.
-
First Solution Search and Local Search:
- Additional “first solution searchers” are launched on remaining threads. These stop once a feasible solution is found.
- Once a feasible solution is discovered, incomplete subsolvers take over, applying local search heuristics such as Large Neighborhood Search (LNS). These subsolvers attempt to improve the solution by iterating through various strategies via a Round Robin approach.
- During each LNS iteration:
- A copy of the model is made, and a solution is selected from the pool of solutions.
- A subset of variables is removed from the solution (the method for choosing this subset varies between strategies). The neighborhood of these variables is then explored for a better solution.
- The remaining variables are fixed to their current values in the copied model.
- The simplified model is presolved with the fixed variables, which often makes the model much easier to solve.
- The simplified model is then solved using a complete strategy, but with a short time limit and on a single thread.
- If a new solution is found, it’s added to the pool of solutions.
-
Solution Transformation:
- The final solution is transformed back into the original model format, allowing you to query the values of the variables as defined in your original model.
This is taken from this talk and slightly extended.
The use of linear programming techniques
As already mentioned before, CP-SAT also utilizes the (dual) simplex algorithm and linear relaxations. The linear relaxation is implemented as a propagator and potentially executed at every node in the search tree but only at lowest priority. A significant difference to the application of linear relaxations in branch and bound algorithms is that only some pivot iterations are performed (to make it faster). However, as there are likely much deeper search trees and the warm-starts are utilized, the optimal linear relaxation may still be computed, just deeper down the tree (note that for SAT-solving, the search tree is usually traversed DFS). At root level, even cutting planes such as Gomory-Cuts are applied to improve the linear relaxation.
The linear relaxation is used for detecting infeasibility (IPs can actually be more powerful than simple SAT, at least in theory), finding better bounds for the objective and variables, and also for making branching decisions (using the linear relaxation’s objective and the reduced costs).
The used Relaxation Induced Neighborhood Search RINS (LNS worker), a very successful heuristic, of course also uses linear programming.
Limitations of CP-SAT
While CP-SAT is undeniably a potent solver, it does possess certain limitations when juxtaposed with alternative techniques:
- While proficient, it may not match the speed of a dedicated SAT-solver when tasked with solving SAT-formulas, although its performance remains quite commendable.
- Similarly, for classical MIP-problems, CP-SAT may not outpace dedicated MIP-solvers in terms of speed, although it still delivers respectable performance.
- Unlike MIP/LP-solvers, CP-SAT lacks support for continuous variables, and the workarounds to incorporate them may not always be highly efficient. In cases where your problem predominantly features continuous variables and linear constraints, opting for an LP-solver is likely to yield significantly improved performance.
- CP-SAT does not offer support for lazy constraints or iterative model building, a feature available in MIP/LP-solvers and select SAT-solvers. Consequently, the application of exponential-sized models, which are common and pivotal in Mixed Integer Programming, may be restricted.
- CP-SAT is limited to the Simplex algorithm and does not feature interior point methods. This limitation prevents it from employing polynomial time algorithms for certain classes of quadratic constraints, such as Second Order Cone constraints. In contrast, solvers like Gurobi utilize the Barrier algorithm to efficiently tackle these constraints in polynomial time.
CP-SAT might also exhibit inefficiency when confronted with certain constraints, such as modulo constraints. However, it’s noteworthy that I am not aware of any alternative solver capable of efficiently addressing these specific constraints. At times, NP-hard problems inherently pose formidable challenges, leaving us with no alternative but to seek more manageable modeling approaches instead of looking for better solvers.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Alternatives
Alternatives: CP-SAT’s Place in the World of Optimization

When you begin exploring optimization, you will encounter a plethora of tools, techniques, and communities. It can be overwhelming, as these groups, while sharing many similarities, also differ significantly. They might use the same terminology for different concepts or different terms for the same concepts, adding to the confusion. Not too many experts can effectively navigate these varied communities and techniques. Often, even specialists, including professors, concentrate on a singular technique or community, remaining unaware of potentially more efficient methods developed in other circles.
If you are interested in understanding the connections between different optimization concepts, consider watching the talk Logic, Optimization, and Constraint Programming: A Fruitful Collaboration by John Hooker. Please note that this is an academic presentation and assumes some familiarity with theoretical computer science.
Let us now explore the various tools and techniques available, and see how they compare to CP-SAT. Please note that this overview is high-level and not exhaustive. If you have any significant additions, feel free to open an issue, and I will consider including them.
- Mixed Integer (Linear) Programming (MIP): MIP is a highly effective method
for solving a variety of optimization problems, particularly those involving
networks like flow or tour problems. While MIP only supports linear
constraints, making it less expressive than CP-SAT, it is often the best
choice if your model is compatible with these constraints. CP-SAT incorporates
techniques from MIP, but with limitations, including the absence of continuous
variables and incremental modeling. Consequently, pure MIP-solvers, being more
specialized, tend to offer greater efficiency for certain applications.
Notable MIP-solvers include:
- Gurobi: A commercial solver known for its state-of-the-art capabilities in MIP-solving. It offers free academic licenses, exceptional performance, user-friendliness, and comprehensive support through documentation and expert-led webinars. Gurobi is particularly impressive in handling complex, large-scale problems.
- SCIP: An open-source solver that provides a Python interface. Although not as efficient or user-friendly as Gurobi, SCIP allows extensive customization and is ideal for research and development, especially for experts needing to implement advanced decomposition techniques. If you know how to use it, you can achieve better performance than any other solver for certain problems (especially with Branch and Price).
- FICO Xpress Optimization: Another popular commercial solver. A lot of the SCIP developers seem to end up either at Gurobi or Xpress.
- COPT Cardinal Solver: A relatively new commercial solver that seems to be very strong for some problem classes.
- HiGHS: A newer solver licensed under MIT, presenting an interesting alternative to SCIP. It is possibly faster and features a more user-friendly interface, but is less versatile. For performance benchmarks, see here.
- Constraint Programming (CP): Constraint Programming is a more general
approach to optimization problems than MIP. As the name suggests, it focuses
on constraints and solvers usually come with a lot of advanced constraints
that can be used to describe your problem more naturally. A classical example
is the
AllDifferent-constraint, which is very hard to model in MIP, but would allow, e.g., to trivially model a Sudoku problem. Constraint Programming has been very successful for example in solving scheduling problems, where you have a lot of constraints that are hard to model with linear constraints. The internal techniques of CP-solvers are often more logic-based and less linear algebra-based than MIP-solvers. Popular CP-solvers are:- OR-Tools’ CP-SAT: Discussed in this primer, CP-SAT combines various optimization techniques, including those from MIP solvers, but its primary technique is Lazy Clause Generation. This approach translates problems into (Max-)SAT formulas for resolution.
- Choco: A traditional CP solver developed in Java, licensed under the BSD 4-Clause. While it may not match CP-SAT in efficiency or modernity, Choco offers significant flexibility, including the option to integrate custom propagators.
- SAT-Solvers: If your problem is actually just to find a feasible solution
for some boolean variables, you may want to use a SAT-solver. SAT-solvers are
surprisingly efficient and can often handle problems with millions of
variables. If you are clever, you can also do some optimization problems with
SAT-solvers, as CP-SAT actually does. Most SAT-solvers support incremental
modelling, and some support cardinality constraints. However, they are pretty
low-level and CP-SAT actually can achieve similar performance for many
problems. A popular library for SAT-solvers is:
- PySAT: PySAT is a Python library under MIT license that provides a nice interface to many SAT-solvers. It is very easy to use and allows you to switch between different solvers without changing your code. It is a good choice if you want to experiment with SAT-solvers.
- There are many solvers popping up every year and many of them are open source. Check out the SAT Competition to see the current state of the art. Most of the solvers are written in C or C++ and do not provide much documentation. However, as SAT-formulas are very simple and the solvers usually do not have complex dependencies, they can still be reasonably easy to use.
- Satisfiability modulo theories (SMT): SMT-solvers represent an advanced
tier above traditional SAT-solvers. They aim to check the satisfiability of
mathematical formulas by extending propositional logic with additional
theories like linear arithmetic, bit-vectors, arrays, and quantifiers. For
instance, an SMT-solver can determine if a formula is satisfiable under
conditions where all variables are integers that meet specific linear
constraints. Similar to the Lazy Clause Generation utilized by CP-SAT,
SMT-solvers usually use a SAT-solver in the backend, extended by complex
encodings and additional propagators to handle an extensive portfolio of
expressions. These solvers are commonly used in automated theorem proving and
system verification. A popular SMT-solver is:
- Z3: Developed by Microsoft and available under the MIT license, Z3 offers a robust Python interface and comprehensive documentation, making it accessible for a variety of applications.
- Nonlinear Programming (NLP): Many MIP-solvers can actually handle some
nonlinear constraints, as people noticed that some techniques are actually
more general than just for linear constraints, e.g., interior points methods
can also solve second-order cone problems. However, you will notice serious
performance downgrades as these non-linearity is much more difficult to
handle. If your constraints and objectives get too complex, they may also no
longer be a viable option. Luckily, there currently is a lot of movement in
this area and you can expect that the big solvers (like Gurobi, COPT, Xpress,
etc.) will get better and better in handling these problems. If you have
smaller optimization problems of (nearly) any kind, you may want to look into:
- SciPy: SciPy is a Python library that offers a wide range of optimization algorithms. Do not expect it to get anywhere near the performance of a specialized solver, but it gives you a bunch of different options to solve a multitude of problems.
- Modeling Languages: Modeling languages provide a high-level, user-friendly
interface for formulating optimization problems, focusing on the challenges of
developing and maintaining models that accurately reflect real-world
scenarios. These languages are solver-agnostic, allowing easy switching
between different solvers - such as from the free SCIP solver to the
commercial Gurobi - without modifying the underlying model. They also
facilitate the use of diverse techniques, like transitioning between
constraint programming and mixed integer programming. However, the trade-off
is a potential loss of control and performance for the sake of generality and
simplicity. Some of the most popular modeling languages include:
- MiniZinc: Very well-documented and free modelling language that seems to have a high reputation especially in the academic community. The amazing course on constraint programming by Pierre Flener also uses MiniZinc. It supports many backends and there are the MiniZinc Challenges, where CP-SAT won quite a lot of medals.
- AMPL: AMPL is possibly the most popular modelling language. It has free and commercial solvers. There is not only extensive documentation, but even a book on how to use it.
- GAMS: This is a commercial system which supports many solvers and also has gotten a Python-interface. I actually know the guys from GAMS as they have a location in Braunschweig. They have a lot of experience in optimization, but I have never used their software myself.
- pyomo: Pyomo is a Python library that allows you to model your optimization problem in Python and then let it solve by different solvers. It is not as high-level as AMPL or GAMS, but it is free and open source. It is also very flexible and allows you to use Python to model your problem, which is a huge advantage if you are already familiar with Python. It actually has support for CP-SAT and could be an option if you just want to have a quick solution.
- OR-Tools’ MathOpt: A very new competitor and sibling of CP-SAT. It only supports a few solvers, but may be still interesting.
- Specialized Algorithms: For many optimization problems, there are
specialized algorithms that can be much more efficient than general-purpose
solvers. Examples are:
- Concorde: Concorde is a solver for the Traveling Salesman Problem that despite its age is still blazingly fast for many instances.
- OR-Tools’ Routing Solver: OR-Tools also comes with a dedicated solver for routing problems.
- OR-Tools’ Network Flows: OR-Tools also comes with a dedicated solver for network flow problems.
- …
- Approximation Algorithms: For many difficult optimization problems, you can find scientific papers that describe approximation algorithms for them. These algorithms come with some guarantees of not being too far off from the optimal solution. Some are even proven to achieve the best possible guarantees. However, you should not directly try to implement such a paper even if it perfectly fits your problem. There are some approximation algorithms that are actually practical, but many are not. The guarantees are usually focussed on artificial worst-case scenarios, and even if the algorithms can be implemented, they may be beaten by simple heuristics. Approximation algorithms and their analysis can be quite useful for understanding the structure of your problem, but their direct practical use is limited.
- Meta-Heuristics: Instead of using a generic solver like CP-SAT, you can also try to build a custom algorithm for your problem based on some meta-heuristic pattern, like simulated annealing, genetic algorithms, or tabu search. Meta-heuristics require some coding, but once you know the pattern, they are quite straightforward to implement. While there are some libraries to generalize parts of the algorithms, you could also just write the whole algorithm yourself. This gives the advantage of truly understanding what is going on in the algorithm, but you miss a lot of advanced techniques contained in solvers like CP-SAT. For many optimization problems, you will have difficulties competing against techniques utilizing advanced solvers in terms of solution quality. If you just want a quick solution, meta-heuristics can be a good start.
As evident, there exists a diverse array of tools and techniques for solving optimization problems. CP-SAT stands out as a versatile approach, particularly well-suited for combinatorial optimization challenges. If you frequently encounter these types of problems, becoming proficient with CP-SAT is highly recommended. Its effectiveness across a broad spectrum of scenarios - excelling in many - is remarkable for a tool that is both free and open-source.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
MathOpt
MathOpt as a Modeling Layer
Google OR-Tools recently introduced a new modeling layer called
MathOpt. It provides a
solver-agnostic API for defining and solving mathematical optimization problems,
especially linear programs (LPs) and mixed-integer programs (MIPs). It is meant
as a simpler and more modern alternative to the older pywraplp interface, with
a stronger focus on usability and performance.
This is exciting because many optimization problems can naturally be formulated as LPs or MIPs, and CP-SAT is not always the right tool for those. As discussed earlier, working with continuous variables and coefficients in CP-SAT is not very convenient, since they have to be discretized carefully. With MathOpt, you can directly use continuous variables and floating-point coefficients when using a solver that supports them (for example, HiGHS or Gurobi). For certain types of problems, LP/MIP solvers can also be much more efficient than CP-SAT. When you model your problem with MathOpt, you can easily switch between different solvers and see which one works best for your case.
What is the catch when using MathOpt? It introduces a small amount of overhead
compared to calling a solver’s native API directly, and it currently supports
only linear constraints—that is, the ones you would add in CP-SAT using the
add method, excluding the !=, <, and > operators. MathOpt itself
supports continuous and unbounded variables as well as floating-point
coefficients, but these features are not available when you select CP-SAT as the
backend. If your model contains continuous variables, you will get an error,
since CP-SAT only supports integer variables and coefficients.
If you want to compare the performance of CP-SAT with a MIP solver, you still need to discretize continuous variables and coefficients when your problem requires it. Fortunately, many practical problems are purely integral, so you might not even notice this limitation in practice.
In the following, I give a brief overview of the MathOpt API.
Import and Model Creation
As in CP-SAT, you first need to import the MathOpt module and create a model instance.
from ortools.math_opt.python import mathopt as mo
model = mo.Model(name="optional_name")
Variables
Next, you can start adding variables to the model. MathOpt supports continuous,
binary, and integer variables. By default, continuous and integer variables are
non-negative (i.e., they have a lower bound of 0). You can specify different
bounds using the lb and ub parameters.
x = model.add_variable(lb=0.0, ub=10.0, name="x") # Continuous variable in [0, 10]
# Unlike CP-SAT, you do not have to name variables
nameless_x = model.add_variable(lb=0.0, ub=10.0) # Nameless variable
x_unbounded = model.add_variable(lb=-math.inf, ub=math.inf, name="x_unbounded") # Unbounded continuous variable
To create binary or integer variables, use the corresponding methods:
y = model.add_binary_variable(name="y") # Binary variable in {0, 1}
z = model.add_integer_variable(lb=0, ub=100, name="z") # Integer variable in [0, 100]
# Integer variable with no upper bound
z_unbounded = model.add_integer_variable(name="z_unbounded")
# or explicitly
z_unbounded = model.add_integer_variable(lb=0, ub=math.inf, name="z_unbounded")
 The default lower bound is 0 for all variables, and the upper bound is
infinity for continuous and integer variables. If you want a variable that can
take negative values, you must explicitly set the lower bound to |
Constraints
You can add linear constraints to the model using the add_linear_constraint
method. There are two ways to do this: the inequality/equality form and the
boxed form.
# Inequality/equality form using Python operators
model.add_linear_constraint(2 * x + 3 * y <= 10, name="constraint1")
model.add_linear_constraint(x + y + z == 5, name="constraint2")
model.add_linear_constraint(z - 2 * x >= 0, name="constraint3")
# Boxed form
model.add_linear_constraint(lb=0, expr=2 * x + 3 * y, ub=10, name="constraint1_boxed")
model.add_linear_constraint(lb=5, expr=x + y + z, ub=5, name="constraint2_boxed") # equality
model.add_linear_constraint(lb=0, expr=z - 2 * x, ub=math.inf, name="constraint3_boxed") # inequality
# Constraints do not have to be named
model.add_linear_constraint(4 * x + y <= 20)
If you want to sum over a list of terms, you can use standard Python sums as in
CP-SAT. However, MathOpt provides a more efficient function, mo.fast_sum,
which is optimized for performance.
terms = [i * x for i in range(1, 11)] # Create a list of terms
model.add_linear_constraint(mo.fast_sum(terms) <= 100, name="sum_constraint")
You can also use expression handles, which can make the model more readable and easier to maintain.
in_vars = [mo.variable(name=f"in_{i}") for i in range(1, 6)]
out_vars = [mo.variable(name=f"out_{i}") for i in range(1, 6)]
incoming_flow = mo.fast_sum(in_vars)
outgoing_flow = mo.fast_sum(out_vars)
model.add_linear_constraint(incoming_flow == outgoing_flow, name="flow_conservation")
Objective
You can define the model’s objective using the set_objective method and
specify whether you want to maximize or minimize it.
model.set_objective(3 * x + 4 * y + 2 * z, is_maximize=True) # Maximize
model.set_objective(x + 2 * z, is_maximize=False) # Minimize
Solving
To solve the model, use the mo.solve function, which takes the model, the
solver type, and optional solver parameters.
params = mo.SolveParameters(
time_limit=timedelta(seconds=30), # Time limit of 30 seconds
relative_gap_tolerance=0.01, # 1% relative gap tolerance
enable_output=True # Enable solver output
)
result = mo.solve(model, solver_type=mo.SolverType.HIGHS, params=params)
MathOpt currently supports the following solvers: GSCIP, GUROBI, GLOP,
CP_SAT, PDLP, GLPK, OSQP, ECOS, SCS, HIGHS, and SANTORINI. If
you do not have a Gurobi license, I recommend using HiGHS or GSCIP, both of
which are open-source mixed-integer programming solvers.
Inspecting Results
After solving the model, you can inspect the results through the SolveResult
object returned by mo.solve.
Check the termination reason:
term = result.termination
print(f"Termination: {term.reason.name}")
if term.detail:
print(f"Detail: {term.detail}")
Check whether a primal feasible solution was found:
if result.has_primal_feasible_solution():
print(f"Objective value: {result.objective_value()}")
values = result.variable_values()
print(f"x: {values.get(x)}, y: {values.get(y)}, z: {values.get(z)}")
else:
print("No primal feasible solution found.")
The variable_values() method returns a mapping from variables to their values.
You can also pass a list of variables to get their values in the same order,
which can be convenient if you only need a subset.
values = result.variable_values([x, y, z])
print(f"x: {values[0]}, y: {values[1]}, z: {values[2]}")
 If you are solving an LP and the underlying solver supports dual values, you
can also access the dual values of the constraints using the |
Examples
Let us look at two examples that demonstrate how to model and solve optimization problems with MathOpt.
Simplified Stigler Diet Problem
The Simplified Stigler Diet Problem is a classical optimization problem in which the goal is to select nonnegative servings of various foods to minimize the total cost while satisfying minimum nutritional requirements for calories, protein, and calcium. This model serves as a small, illustrative example of how mathematical optimization can be applied to dietary planning. The units and values used here are for demonstration purposes only and should not be interpreted as nutritional facts.
from ortools.math_opt.python import mathopt as mo
from datetime import timedelta
# --- Data -----------------------------------------------------------------
foods = ["Wheat Flour", "Milk", "Cabbage", "Beef"]
# Cost per serving (EUR)
cost = {
"Wheat Flour": 0.36,
"Milk": 0.23,
"Cabbage": 0.10,
"Beef": 1.20,
}
# Nutrients per serving (approximate / illustrative)
# Calories Protein(g) Calcium(mg)
calories = {"Wheat Flour": 364.0, "Milk": 150.0, "Cabbage": 25.0, "Beef": 250.0}
protein = {"Wheat Flour": 10.0, "Milk": 8.0, "Cabbage": 1.3, "Beef": 26.0}
calcium = {"Wheat Flour": 15.0, "Milk": 285.0, "Cabbage": 40.0, "Beef": 20.0}
# Minimum requirements
req = {
"Calories": 2000.0, # kcal
"Protein": 55.0, # g
"Calcium": 800.0, # mg
}
# --- Model ----------------------------------------------------------------
model = mo.Model(name="stigler_diet")
# Decision: servings of each food (continuous, ≥ 0)
# You could switch to integers to create a MIP variant.
servings = {f: model.add_variable(lb=0.0, name=f"servings[{f}]") for f in foods}
# Optional upper bounds to keep results tidy
for f in foods:
model.add_linear_constraint(servings[f] <= 20.0, name=f"cap[{f}]")
# --- Nutrient constraints --------------------------------------------------
model.add_linear_constraint(
mo.fast_sum(calories[f] * servings[f] for f in foods) >= req["Calories"],
name="nutrients[Calories]",
)
model.add_linear_constraint(
mo.fast_sum(protein[f] * servings[f] for f in foods) >= req["Protein"],
name="nutrients[Protein]",
)
model.add_linear_constraint(
mo.fast_sum(calcium[f] * servings[f] for f in foods) >= req["Calcium"],
name="nutrients[Calcium]",
)
# --- Objective: minimize total cost ---------------------------------------
model.set_objective(
mo.fast_sum(cost[f] * servings[f] for f in foods),
is_maximize=False,
)
# --- Solve ----------------------------------------------------------------
params = mo.SolveParameters(
time_limit=timedelta(seconds=10),
relative_gap_tolerance=1e-6, # LP, so we can be tight
enable_output=False,
)
result = mo.solve(model, solver_type=mo.SolverType.HIGHS, params=params)
# --- Report ----------------------------------------------------------------
term = result.termination
print(f"Termination: {term.reason.name}")
if not result.has_primal_feasible_solution():
print("No feasible solution found.")
return
print(f"Minimum cost: €{result.objective_value():.2f}")
# Extract chosen servings (suppress near-zeros)
values = result.variable_values()
print("\nServings:")
for f in foods:
qty = values.get(servings[f], 0.0)
if abs(qty) > 1e-9:
print(f" {f:12s}: {qty:8.3f}")
# Compute realized totals
tot_cal = sum(calories[f] * values.get(servings[f], 0.0) for f in foods)
tot_pro = sum(protein[f] * values.get(servings[f], 0.0) for f in foods)
tot_calcium = sum(calcium[f] * values.get(servings[f], 0.0) for f in foods)
print("\nNutrient totals (minimum required in parentheses):")
print(f" Calories: {tot_cal:.1f} ({req['Calories']})")
print(f" Protein : {tot_pro:.1f} ({req['Protein']})")
print(f" Calcium : {tot_calcium:.1f} ({req['Calcium']})")
Set Cover
The Set Cover Problem is a classic combinatorial optimization problem. Given a universe \( U \) of elements and a collection of subsets \( S \subseteq 2^U \), each with an associated integer cost, the goal is to select a minimum-cost collection of subsets such that every element in \( U \) is covered by at least one selected subset.
This problem appears in resource allocation, scheduling, and network design. A standard integer formulation is:
- Variables: For each subset \( S \), a binary variable \( z[S] \in {0, 1} \) indicates whether subset \( S \) is chosen.
- Constraints: For each element \( u \in U \), the sum of \( z[S] \) over all subsets \( S \) containing \( u \) must be at least 1.
- Objective: Minimize the total cost \( \sum_{S} \text{cost}[S] \cdot z[S] \).
Since all variables are integral, this problem can be modeled using CP-SAT and compared directly with MIP solvers such as Gurobi or HiGHS.
from ortools.math_opt.python import mathopt as mo
from datetime import timedelta
U = {1, 2, 3, 4, 5, 6}
subsets = {
"S1": {1, 2, 3},
"S2": {2, 4},
"S3": {3, 5, 6},
"S4": {1, 4, 6},
"S5": {2, 5},
"S6": {4, 5, 6},
}
cost = {"S1": 4, "S2": 2, "S3": 3, "S4": 3, "S5": 2, "S6": 4}
model = mo.Model(name="set_cover_cp_sat")
# Decision variables
z = {s: model.add_binary_variable(name=f"pick[{s}]") for s in subsets}
# Cover constraints
for u in U:
model.add_linear_constraint(
mo.fast_sum(z[s] for s in subsets if u in subsets[s]) >= 1,
name=f"cover[{u}]",
)
# Objective
model.set_objective(
mo.fast_sum(cost[s] * z[s] for s in subsets),
is_maximize=False,
)
# Solve with CP-SAT
params = mo.SolveParameters(time_limit=timedelta(seconds=10), enable_output=True)
result = mo.solve(model, solver_type=mo.SolverType.CP_SAT, params=params)
print(f"[SetCover] Termination: {result.termination.reason.name}")
if not result.has_primal_feasible_solution():
print("[SetCover] No feasible solution found.")
return
vals = result.variable_values()
chosen = [s for s in subsets if int(round(vals.get(z[s], 0.0)))]
total_cost = sum(cost[s] for s in chosen)
print(f"[SetCover] Minimum total cost: {total_cost}")
print("[SetCover] Chosen subsets:", ", ".join(chosen))
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Part 2: Advanced Topics
Coding Patterns for Optimization Problems

In this chapter, we will explore various coding patterns that help you structure your implementations for optimization problems using CP-SAT. These patterns become especially useful when working on complex problems that need to be solved continuously and potentially under changing requirements. While we specifically focus on CP-SAT’s Python API, many patterns can be adapted to other solvers and languages.
In many cases, specifying the model and solving it is sufficient without the need for careful structuring. However, there are situations where your models are complex and require frequent iteration, either for performance reasons or due to changing requirements. In such cases, it is crucial to have a good structure in place to ensure that you can easily modify and extend your code without breaking it, as well as to facilitate testing and comprehension. Imagine you have a complex model and need to adapt a constraint due to new requirements. If your code is not modular and your test suite is only able to test the entire model, this small change will force you to rewrite all your tests. After a few iterations, you might end up skipping the tests altogether, which is a dangerous path to follow.
Another common issue in complex optimization models is the risk of forgetting to add some trivial constraints to interlink auxiliary variables, which can render parts of the model dysfunctional. If the dysfunctional part concerns feasibility, you might still notice it if you have separately checked the feasibility of the solution. However, if it involves the objective, such as penalizing certain combinations, you may not easily notice that your solution is suboptimal, as the penalties are not applied. Furthermore, implementing complex constraints can be challenging, and a modular structure allows you to test these constraints separately to ensure they work as intended. Test-driven development (TDD) is an effective approach for implementing complex constraints quickly and reliably.
The field of optimization is highly heterogeneous, and the percentage of optimizers with a professional software engineering background seems surprisingly low. Much of the optimization work is done by mathematicians, physicists, and engineers who have deep expertise in their fields but limited experience in software engineering. They are usually highly skilled and can create excellent models, but their code is often not very maintainable and does not follow software engineering best practices. Many problems are similar enough that minimal explanation or structure is deemed sufficient—much like creating plots by copying, pasting, and adjusting a familiar template. While this approach may not be very readable, it is familiar enough for most people in the field to understand. Additionally, it is typical for mathematicians to first document the model and then implement it. From a software engineering perspective, this workflow resembles the waterfall model, which lacks agility.
There appears to be a lack of literature on agile software development in optimization, which this chapter seeks to address by presenting some patterns I have found useful in my work. I asked a few senior colleagues in the field, and unfortunately, they could not provide any useful resources either or did not even see the need for such resources. For many use cases, the simple approach is indeed sufficient. However, I have found that these patterns make my agile, test-driven workflow much easier, faster, and more enjoyable. Note that this chapter is largely based on my personal experience due to the limited availability of references. I would be happy to hear about your experiences and the patterns you have found useful in your work.
In the following sections, we will start with the basic function-based pattern and then introduce further concepts and patterns that I have found valuable. We will work on simple examples where the benefits of these patterns may not be immediately apparent, but I hope you will see their potential in more complex problems. The alternative would have been to provide complex examples, which might have distracted from the patterns themselves.
 The following patterns focus on details specific to computational
optimization. However, many optimization engineers come from mathematics or
physics backgrounds and may not have professional Python or software
engineering experience. If you are among them, I recommend familiarizing
yourself in especially with
basic data structures and their comprehensions
and elegant loops using
itertools. These tools
allow you to express your mathematical ideas in Python more elegantly in
general, and they are especially useful for optimization problems.
Additionally, there are excellent tools to automatically format, check, and
improve your code, such as ruff.
Regularly running |
Simple Function
For straightforward optimization problems, encapsulating the model creation and solving within a single function is a practical approach. This method is best suited for simpler cases due to its straightforward nature but lacks flexibility for more complex scenarios. Parameters such as the time limit and optimality tolerance can be customized via keyword arguments with default values.
The following Python function demonstrates solving a simple knapsack problem using CP-SAT. To recap, in the knapsack problem, we select items - each with a specific weight and value - to maximize total value without exceeding a predefined weight limit. Given its simplicity, involving only one constraint, the knapsack problem serves as an ideal model for introductory examples.
from ortools.sat.python import cp_model
from typing import List
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*,
time_limit: int = 900,
opt_tol: float = 0.01,
) -> List[int]:
# initialize the model
model = cp_model.CpModel()
n = len(weights) # Number of items
# Decision variables for items
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
# Capacity constraint
model.add(sum(weights[i] * x[i] for i in range(n)) <= capacity)
# Objective function to maximize value
model.maximize(sum(values[i] * x[i] for i in range(n)))
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
status = solver.solve(model)
# Extract solution
return (
# Return indices of selected items
[i for i in range(n) if solver.value(x[i])]
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]
else []
)
You can also add some more flexibility by allowing any solver parameters to be passed to the solver.
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*,
time_limit: int = 900,
opt_tol: float = 0.01,
**kwargs,
) -> List[int]:
# initialize the model
model = cp_model.CpModel()
# ...
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
for key, value in kwargs.items():
setattr(solver.parameters, key, value)
# ...
Add some unit tests in some separate file (e.g., test_knapsack.py) to ensure
that the model works as expected.
 Write the tests before you write the code. This approach is known as test-driven development (TDD) and can help you to structure your code better and to ensure that your code works as expected. It also helps you to think about the API of your function before you start implementing it. |
# Make sure you have a proper project structure and can import your function
from myknapsacksolver import solve_knapsack
def test_knapsack_empty():
# Always good to have a test for the trivial case. The more trivial the
# case, the more likely it is that you forget it.
assert solve_knapsack([], [], 0) == []
def test_knapsack_nothing_fits():
# If nothing fits, we should get an empty solution
assert solve_knapsack([10, 20, 30], [1, 2, 3], 5) == []
def test_knapsack_one_item():
# If only one item fits, we should get this item
assert solve_knapsack([10, 20, 30], [1, 2, 3], 10) == [0]
def test_knapsack_all_items():
# If all items fit, we should get all items
assert solve_knapsack([10, 20, 30], [1, 2, 3], 100) == [0, 1, 2]
Using pytest, you can run all tests in the project with pytest .. Check
Real Python for a good tutorial
on pytest.
Logging the Model Building
When working with larger optimization problems, logging the model-building process can be essential to find and fix issues. Often, the problem lies not within the solver but in the model building itself.
In the following example, we add some basic logging to the solver function to give us some insights into the model-building process. This logging can be easily activated or deactivated by the logging framework, allowing us to use it not only during development but also in production, where you usually deactivate a lot of logging to save resources.
If you do not know about the logging framework of Python, this is an excellent
moment to learn about it. I consider it an essential skill for production code
and this and similar frameworks are used for most production code in any
language. The official Python documentation contains a
good tutorial. There are people
that prefer other logging frameworks, but it comes with Python and is good
enough for most use cases, definitely better than using the badly configurable
print statement.
import logging
from ortools.sat.python import cp_model
from typing import List
# Configure the logging framework if it is not already configured.
# We are setting it to debug level, as we are still developing the code.
logging.basicConfig(format="%(asctime)s - %(message)s", level=logging.DEBUG)
_logger = logging.getLogger(__name__) # get a logger for the current module
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*, # Make the following arguments keyword-only
time_limit: int = 900,
opt_tol: float = 0.01,
) -> List[int]:
_logger.debug("Building the knapsack model")
# initialize the model
model = cp_model.CpModel()
n = len(weights) # Number of items
_logger.debug("Number of items: %d", n)
if n > 0:
if _logger.isEnabledFor(logging.DEBUG):
# Only calculate min, mean, and max if we actually log it
_logger.debug(
"Min/Mean/Max weight: %d/%.2f/%d",
min(weights),
sum(weights) / n,
max(weights),
)
_logger.debug(
"Min/Mean/Max value: %d/%.2f/%d", min(values), sum(values) / n, max(values)
)
# Decision variables for items
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
# Capacity constraint
model.add(sum(weights[i] * x[i] for i in range(n)) <= capacity)
# Objective function to maximize value
model.maximize(sum(values[i] * x[i] for i in range(n)))
# Log the model
_logger.debug("Model created with %d items", n)
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
_logger.debug(
"Starting the solution process with time limit %d seconds", time_limit
)
status = solver.solve(model)
# Extract solution
selected_items = (
[i for i in range(n) if solver.value(x[i])]
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]
else []
)
_logger.debug("Selected items: %s", selected_items)
return selected_items
We will not use logging in the following examples to save space, but you should consider adding it to your code.
 A great hack you can do with the logging framework is that you can easily hook
into your code and do analysis beyond the simple logging. You can simply write
a handler that, e.g., waits for the tag |
Custom Data Classes for Instances, Configurations, and Solutions
Incorporating serializable data classes based on strict schema to manage instances, configurations, and solutions significantly enhances code readability and maintainability. These classes also facilitate documentation, testing, and ensure data consistency across larger projects where data exchange among different components is necessary.
One popular library for this purpose is Pydantic. It is easy to use and provides substantial functionality out of the box. The following code introduces data classes for the instance, configuration, and solution of the knapsack problem. While Python’s duck typing is great for rapidly developing internal data flow, it can be problematic for interfaces. Users will often misuse the interface in unexpected ways, and you will be blamed for it. Pydantic helps mitigate these issues by providing a clear interface and validating input data. Additionally, you can create an API for your code effortlessly using FastAPI, which is built on top of Pydantic.
# pip install pydantic
from pydantic import (
BaseModel,
PositiveInt,
NonNegativeFloat,
PositiveFloat,
Field,
model_validator,
)
class KnapsackInstance(BaseModel):
# Defines the knapsack instance to be solved.
weights: list[PositiveInt] = Field(..., description="The weight of each item.")
values: list[PositiveInt] = Field(..., description="The value of each item.")
capacity: PositiveInt = Field(..., description="The capacity of the knapsack.")
@model_validator(mode="after")
def check_lengths(cls, v):
if len(v.weights) != len(v.values):
raise ValueError("Mismatch in number of weights and values.")
return v
class KnapsackSolverConfig(BaseModel):
# Defines the configuration for the knapsack solver.
time_limit: PositiveFloat = Field(
default=900.0, description="Time limit in seconds."
)
opt_tol: NonNegativeFloat = Field(
default=0.01, description="Optimality tolerance (1% gap allowed)."
)
log_search_progress: bool = Field(
default=False, description="Whether to log the search progress."
)
class KnapsackSolution(BaseModel):
# Defines the solution of the knapsack problem.
selected_items: list[int] = Field(..., description="Indices of selected items.")
objective: float = Field(..., description="Objective value of the solution.")
upper_bound: float = Field(
..., description="Upper bound of the solution, i.e., a proven limit on how good a solution could be."
)
 Your data schema should be fully prepared for the optimization process, requiring no further preprocessing. Data preparation and optimization are both complex tasks, and combining them can significantly increase complexity, making your code difficult to maintain. Ideally, your optimization code should simply iterate over the data and add the corresponding constraints and objectives to the model. |
The original code needs to be adapted to use these data classes.
from ortools.sat.python import cp_model
def solve_knapsack(
instance: KnapsackInstance, config: KnapsackSolverConfig
) -> KnapsackSolution:
model = cp_model.CpModel()
n = len(instance.weights)
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
model.add(sum(instance.weights[i] * x[i] for i in range(n)) <= instance.capacity)
model.maximize(sum(instance.values[i] * x[i] for i in range(n)))
solver = cp_model.CpSolver()
# Set solver parameters from the configuration
solver.parameters.max_time_in_seconds = config.time_limit
solver.parameters.relative_gap_limit = config.opt_tol
solver.parameters.log_search_progress = config.log_search_progress
# Solve the model and return the solution
status = solver.solve(model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=[i for i in range(n) if solver.value(x[i])],
objective=solver.objective_value,
upper_bound=solver.best_objective_bound,
)
return KnapsackSolution(selected_items=[], objective=0, upper_bound=0)
You can use the serialization and deserialization capabilities of Pydantic to quickly generate test cases based on real data. While you cannot be certain that your code is correct with such tests, they will at least notify you if the logic changes unexpectedly. If you refactor your code, you will immediately see if its behavior changes accidentally.
from datetime import datetime
from hashlib import md5
from pathlib import Path
def add_test_case(instance: KnapsackInstance, config: KnapsackSolverConfig):
"""
Quickly generate a test case based on the instance and configuration.
"""
test_folder = Path(__file__).parent / "test_data"
unique_id = (
datetime.now().strftime("%Y-%m-%d-%H-%M-%S")
+ "_"
+ md5(
(instance.model_dump_json() + config.model_dump_json()).encode()
).hexdigest()
)
subfolder = test_folder / "knapsack" / unique_id
subfolder.mkdir(parents=True, exist_ok=True)
with open(subfolder / "instance.json", "w") as f:
f.write(instance.model_dump_json())
with open(subfolder / "config.json", "w") as f:
f.write(config.model_dump_json())
solution = solve_knapsack(instance, config)
with open(subfolder / "solution.json", "w") as f:
f.write(solution.model_dump_json())
def test_saved_test_cases():
test_folder = Path(__file__).parent / "test_data"
for subfolder in test_folder.glob("knapsack/*"):
with open(subfolder / "instance.json") as f:
instance = KnapsackInstance.model_validate_json(f.read())
with open(subfolder / "config.json") as f:
config = KnapsackSolverConfig.model_validate_json(f.read())
with open(subfolder / "solution.json") as f:
solution = KnapsackSolution.model_validate_json(f.read())
new_solution = solve_knapsack(instance, config)
assert (
new_solution.objective <= solution.upper_bound
), "New solution is better than the previous upper bound: One has to be wrong."
assert (
solution.objective <= new_solution.upper_bound
), "Old solution is better than the new upper bound: One has to be wrong."
# Do not test for the selected items, as the solver might return a different solution of the same quality
You can now easily generate test cases and validate them with the following code. Ideally, you should use real instances for this, potentially by automatically saving 1% of the instances used in production.
# Define a knapsack instance
instance = KnapsackInstance(
weights=[23, 31, 29, 44, 53, 38, 63, 85, 89, 82],
values=[92, 57, 49, 68, 60, 43, 67, 84, 87, 72],
capacity=165,
)
# Define a solver configuration
config = KnapsackSolverConfig(
time_limit=10.0, opt_tol=0.01, log_search_progress=False
)
# Solve the knapsack problem
solution = solve_knapsack(instance, config)
# Add the test case to the test data folder
add_test_case(instance, config)
You can also maintain backward compatibility easily by adding default values to any new fields you add to the data classes.
 One challenge I often face is designing data classes to be as generic as possible so that they can be used with multiple solvers and remain compatible throughout various stages of the optimization process. For instance, a graph might be represented as an edge list, an adjacency matrix, or an adjacency list, each with its own pros and cons, complicating the decision of which format is optimal for all stages. However, converting between different data class formats is typically straightforward, often requiring only a few lines of code and having a negligible impact compared to the optimization process itself. Therefore, I recommend focusing on functionality with your current solver without overcomplicating this aspect. There is little harm in having to call a few conversion functions because you created separate specialized data classes. |
Solver Class
In many real-world optimization scenarios, problems may require iterative refinement of the model and solution. For instance, new constraints might only become apparent after presenting an initial solution to a user or another algorithm (like a physics simulation, which is to complex to optimize directly on). In such cases, flexibility is crucial, making it beneficial to encapsulate both the model and the solver within a single class. This setup facilitates the dynamic addition of constraints and subsequent re-solving without needing to rebuild the entire model, potentially even utilizing warm-starting techniques to improve performance.
We introduce the KnapsackSolver class, which encapsulates the entire setup and
solving process of the knapsack problem. We also use the opportunity to directly
split the model-building into smaller methods, which can be useful for more
complex models.
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self.n = len(instance.weights)
self.x = [self.model.new_bool_var(f"x_{i}") for i in range(self.n)]
self._build_model()
self.solver = cp_model.CpSolver()
def _add_constraints(self):
used_weight = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.add(used_weight <= self.instance.capacity)
def _add_objective(self):
self.model.maximize(
sum(value * x_i for value, x_i in zip(self.instance.values, self.x))
)
def _build_model(self):
self._add_constraints()
self._add_objective()
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def prohibit_combination(self, item_a: int, item_b: int):
"""
Prohibit the combination of two items in the solution.
This can be useful if, after presenting the solution to the user, they decide that these two items should not be packed together. After calling this method, you can simply call `solve` again to get a new solution obeying this constraint.
"""
self.model.add(self.x[item_a] + self.x[item_b] <= 1)
At first glance, this may look like a cumbersome interface, as we first have to
create a solver object for a specific instance and then call the solve method.
However, this structure accommodates many use cases, and I use variations of it
for most of my projects. Additionally, I sometimes add a simple function that
wraps the solver class to make it easier to use for simple cases.
instance = KnapsackInstance(weights=[1, 2, 3], values=[4, 5, 6], capacity=3)
config = KnapsackSolverConfig(time_limit=10, opt_tol=0.01, log_search_progress=True)
solver = KnapsackSolver(instance, config)
solution = solver.solve()
print(solution)
# Check the solution in a more realistic simulation.
# Assume that the simulation now notices that for some more complex reason,
# we could not express in the optimization model, the first two items should
# not be packed together. We can now prohibit this combination and solve again.
solver.prohibit_combination(0, 1)
# Solve the problem again with the new constraint, but this time
# only allow 5 seconds for the solver.
solution = solver.solve(time_limit=5)
print(solution)
Although reusing the solver class primarily spares us from rebuilding the model,
each call to solve still initiates a new search from scratch. However,
iteratively refining the model within the same solver instance is more intuitive
to code than treating each iteration as an entirely new problem. Moreover, as we
will demonstrate next, this pattern allows us to improve performance by
leveraging features like warm-starting — offering advantages over stateless
optimization functions.
Improving Performance with Warm-Starts
As the solver class retains a state and can remember the previous iterations, we can easily add optimizations that would be cumbersome to implement in a stateless function. One such optimization is warm-starting, where the solver uses the previous solution as a starting point or “hint” for the next iteration. This technique can significantly speed up the solving process, as the solver can often use the previous solution as a good starting point for repair, even if the previous solution becomes infeasible due to a newly added constraint. This will of course only have an advantage if the added constraint does not change the problem fundamentally but only requires a part of the solution to be changed.
Because repairing an infeasible hint can be computationally expensive, CP-SAT
handles this process carefully. You can instruct CP-SAT to attempt repairing the
hint by setting solver.parameters.repair_hint = True. Additionally, you can
adjust the limit on how much effort CP-SAT should spend repairing the hint using
solver.parameters.hint_conflict_limit. For example, setting
solver.parameters.hint_conflict_limit = 10 controls how many conflicts CP-SAT
will resolve before giving up.
Here is an example of how to implement this in code:
class KnapsackSolver:
# ...
def _set_solution_as_hint(self):
"""Use the current solution as a hint for the next solve."""
for i, v in enumerate(self.model.proto.variables):
v_ = self.model.get_int_var_from_proto_index(i)
assert v.name == v_.name, "Variable names should match"
self.model.add_hint(v_, self.solver.value(v_))
# Tell CP-SAT to repair the hint if it is infeasible
self.solver.parameters.repair_hint = True
self.solver.parameters.hint_conflict_limit = 20
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
# There is a solution, set it as a hint for the next solve
self._set_solution_as_hint()
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
# ...
To further improve this approach, you could add a heuristic to repair the hint. A feasible hint is much more valuable than one that needs significant repair. For instance, if the hint is infeasible due to a prohibited combination of items, you could simply drop the least valuable item to make the hint valid.
 A common mistake when trying to improve the performance of iterative optimization is adding the previous bound as a constraint. Although this approach might let CP-SAT resume directly from the previous bound, it often limits CP-SAT’s ability to find better solutions. This happens because it adds a strong constraint unrelated to the problem’s feasibility, which can interfere with various internal algorithms (such as reducing the effectiveness of linear relaxation). If bounds significantly affect performance, consider using a callback to check if the current objective is sufficiently close to the previous bound and stop the search if it is. This approach avoids interfering with CP-SAT’s optimization capabilities, though callbacks do introduce some overhead. |
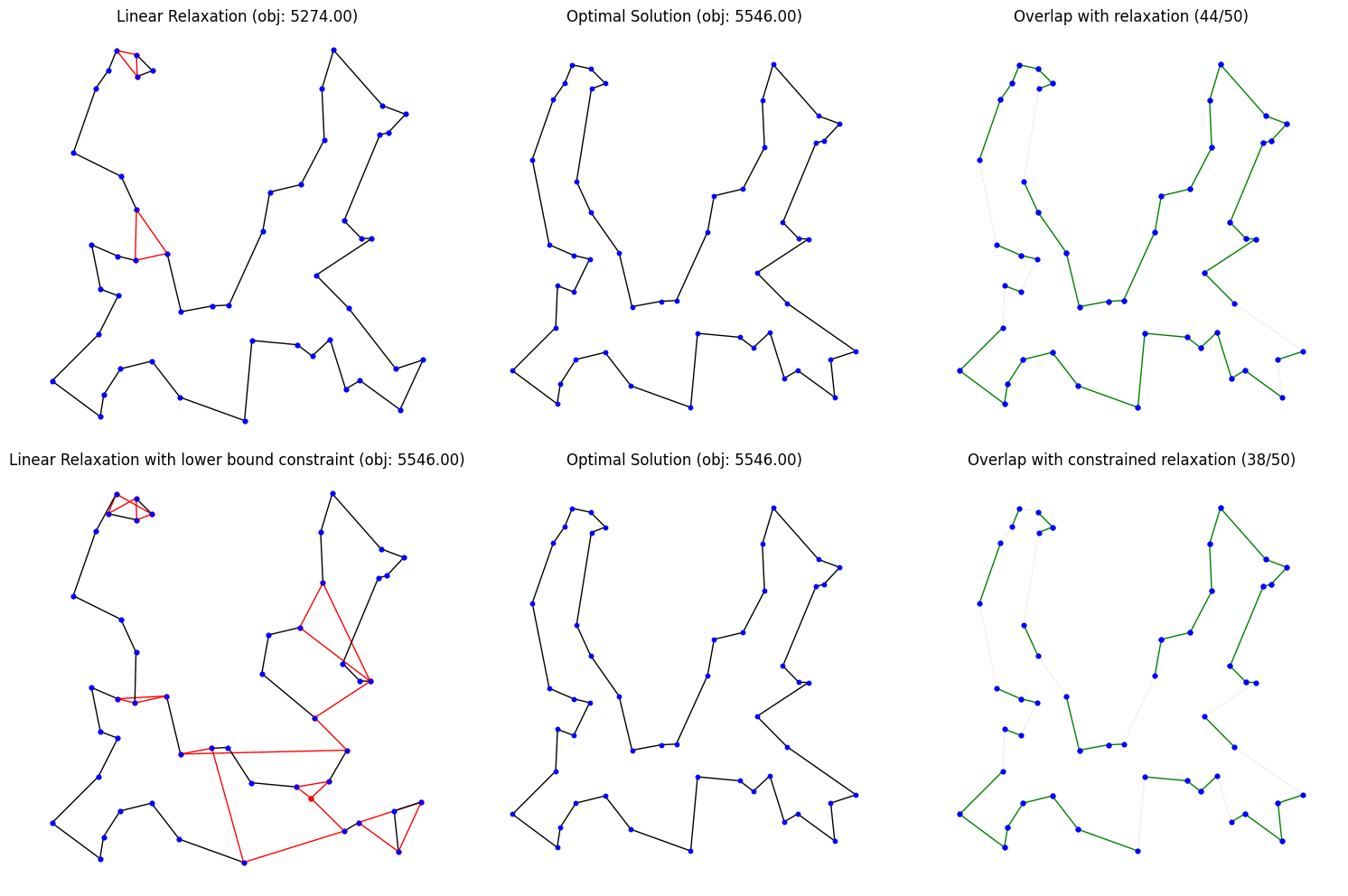 |
|---|
| This image illustrates the detrimental impact of introducing a lower bound constraint into the model on the example of the TSP. The linear relaxation visibly deteriorates: while the original relaxation coincided with the optimal solution on 44 of 50 edges, the relaxation incorporating the lower bound constraint (set to the optimal value) coincides on only 38 edges and exhibits significantly more fractional values. Branching on certain edges may also cease to provide meaningful guidance; unless one branches on a poorly chosen edge, the objective value often remains unchanged as it is dominated by the lower bound constraint. In addition to the reduced informational value of the relaxation, such constraints are also notorious for introducing numerical instabilities (however, CP-SAT is likely unaffected by this issue due to its reliance on integer arithmetic). |
Exchangeable Objective / Multi-Objective Optimization
In real-world scenarios, objectives are often not clearly defined. Typically, there are multiple objectives with different priorities, making it challenging to combine them. Consider the Knapsack problem, representing a logistics issue where we aim to transport the maximum value of goods in a single trip. Given the values and weights of the goods, our primary objective is to maximize the packed goods’ value. However, after computing and presenting the solution, we might be asked to find an alternative solution that does not fill the truck as much, even if it means accepting up to a 5% decrease in value.
 |
|---|
| Which fruit is the best one? Many problems are multi-objective and there is no clear single objective. By xkcd (CC BY-NC 2.5) |
To handle this, we can optimize in two phases. First, we maximize the value under the weight constraint. Next, we add a constraint that the value must be at least 95% of the initial solution’s value and change the objective to minimize the weight. This iterative process can continue through multiple phases, exploring the Pareto front of the two objectives. More complex problems can be tackled using similar approaches.
A challenge with this method is avoiding the creation of multiple models and restarting from scratch in each phase. Since we have a solution close to the new one and changing the objective does not influence feasibility, it is an excellent opportunity to use the current solution as a hint for the next solve.
The following code demonstrates how to extend a solver class to support exchangeable objectives. It includes fixing the current objective value to prevent degeneration and using the current solution as a hint.
We created a member _objective to store the current objective function and
added methods to set the objective to maximize value or minimize weight. We also
introduced methods to set the solution as a hint for the next solve which will
automatically be called if the solve found a feasible solution. To not
degenerate on previous objectives, we added a method to fix the current
objective value based on some ratio.
class MultiObjectiveKnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self.n = len(instance.weights)
self.x = [self.model.new_bool_var(f"x_{i}") for i in range(self.n)]
self._objective = 0
self._build_model()
self.solver = cp_model.CpSolver()
def set_maximize_value_objective(self):
"""Set the objective to maximize the value of the packed goods."""
self._objective = sum(
value * x_i for value, x_i in zip(self.instance.values, self.x)
)
self.model.maximize(self._objective)
def set_minimize_weight_objective(self):
"""Set the objective to minimize the weight of the packed goods."""
self._objective = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.minimize(self._objective)
def _set_solution_as_hint(self):
"""Use the current solution as a hint for the next solve."""
for i, v in enumerate(self.model.proto.variables):
v_ = self.model.get_int_var_from_proto_index(i)
assert v.name == v_.name, "Variable names should match"
self.model.add_hint(v_, self.solver.value(v_))
def fix_current_objective(self, ratio: float = 1.0):
"""Fix the current objective value to prevent degeneration."""
if ratio == 1.0:
self.model.add(self._objective == self.solver.objective_value)
elif ratio > 1.0:
self.model.add(self._objective <= ceil(self.solver.objective_value * ratio))
else:
self.model.add(
self._objective >= floor(self.solver.objective_value * ratio)
)
def _add_constraints(self):
"""Add the weight constraint to the model."""
used_weight = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.add(used_weight <= self.instance.capacity)
def _build_model(self):
"""Build the initial model with constraints and objective."""
self._add_constraints()
self.set_maximize_value_objective()
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
"""Solve the knapsack problem and return the solution."""
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
self._set_solution_as_hint()
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
We can use the MultiObjectiveKnapsackSolver class as follows:
config = KnapsackSolverConfig(time_limit=15, opt_tol=0.01, log_search_progress=True)
solver = MultiObjectiveKnapsackSolver(instance, config)
solution_1 = solver.solve()
# maintain at least 95% of the current objective value
solver.fix_current_objective(0.95)
# change the objective to minimize the weight
solver.set_minimize_weight_objective()
solution_2 = solver.solve(time_limit=10)
There are more advanced and precise methods for computing the Pareto front, but multi-objective optimization is a complex field of research in its own right. If your problem is already challenging with a single objective, adding more objectives will only increase the difficulty.
Using the shown approach of lexicographic optimization (with relaxation) or combining multiple objectives into a single one, for example by adding them with different weights, is often a reasonable compromise. You could also use heuristics to explore the solution space around an initial solution obtained with CP-SAT.
However, multi-objective optimization remains a challenging topic, and even experts rely on significant trial and error to achieve satisfactory results, as compromises are often unavoidable.
Variable Containers
In complex models, variables play a crucial role and can span the entire model. While managing variables as a list or dictionary may suffice for simple models, this approach becomes cumbersome and error-prone as the model’s complexity increases. A single mistake in indexing can introduce subtle errors, potentially leading to incorrect results that are difficult to trace.
As variables form the foundation of the model, refactoring them becomes more challenging as the model grows. Therefore, it is crucial to establish a robust management system early on. Encapsulating variables in a dedicated class ensures that they are always accessed correctly. This approach also allows for the easy addition of new variables or modifications in their management without altering the entire model.
Furthermore, incorporating clear query methods helps maintain the readability and manageability of constraints. Readable constraints, free from complex variable access patterns, ensure that the constraints accurately reflect the intended model.
In the following code, we introduce the _ItemSelectionVars class to the
KnapsackSolver, which acts as a container for the decision variables
associated with the knapsack items. This class not only creates these variables
but also offers several utility methods to interact with them, improving the
clarity and maintainability of the code.
from typing import Generator, Tuple, List
class _ItemSelectionVars:
def __init__(self, instance: KnapsackInstance, model: cp_model.CpModel, var_name: str = "x"):
self.instance = instance
self.x = [model.new_bool_var(f"{var_name}_{i}") for i in range(len(instance.weights))]
def __getitem__(self, i: int) -> cp_model.IntVar:
return self.x[i]
def packs_item(self, i: int) -> cp_model.IntVar:
return self.x[i]
def extract_packed_items(self, solver: cp_model.CpSolver) -> List[int]:
return [i for i, x_i in enumerate(self.x) if solver.value(x_i)]
def used_weight(self) -> cp_model.LinearExprT:
return sum(weight * x_i for weight, x_i in zip(self.instance.weights, self.x))
def packed_value(self) -> cp_model.LinearExprT:
return sum(value * x_i for value, x_i in zip(self.instance.values, self.x))
def iter_items(
self,
weight_lb: float = 0.0,
weight_ub: float = float("inf"),
value_lb: float = 0.0,
value_ub: float = float("inf"),
) -> Generator[Tuple[int, cp_model.IntVar], None, None]:
"""
An example for a more complex query method, which would allow use to
iterate over all items that fulfill certain conditions.
"""
for i, (weight, x_i) in enumerate(zip(self.instance.weights, self.x)):
if (
weight_lb <= weight <= weight_ub
and value_lb <= self.instance.values[i] <= value_ub
):
yield i, x_i
This class can be used in the KnapsackSolver that handles the higher level
logic, i.e., the high level specification of what the model should do, while
details can be hidden in the container class.
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self._item_vars = _ItemSelectionVars(instance, self.model)
self._build_model()
self.solver = cp_model.CpSolver()
def _add_constraints(self):
self.model.add(self._item_vars.used_weight() <= self.instance.capacity)
def _add_objective(self):
self.model.maximize(self._item_vars.packed_value())
def _build_model(self):
self._add_constraints()
self._add_objective()
def solve(self) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=self._item_vars.extract_packed_items(self.solver),
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def prohibit_combination(self, item_a: int, item_b: int):
self.model.add_at_most_one(self._item_vars.packs_item(item_a),
self._item_vars.packs_item(item_b))
For example,
self.model.add(self._item_vars.used_weight() <= self.instance.capacity) now
directly expresses what the constraint does, making the code more readable and
less error-prone. You can actually hide additional optimizations in the
container class, without influencing the higher-level code in the actual solver.
For example, the container class could decide to automatically replace all item
variables that cannot fit into the knapsack due to their weight with a constant.
You can also reuse the variable type, e.g., if you suddenly have two knapsacks to fill. The following code demonstrates how to quickly extend the solver to handle two knapsacks, without sacrificing readability or maintainability.
class KnapsackSolver:
def __init__(self, # ...
):
#...
self._knapsack_a = _ItemSelectionVars(instance, self.model, var_name="x1")
self._knapsack_b = _ItemSelectionVars(instance, self.model, var_name="x2")
#...
def _add_constraints(self):
self.model.add(self._knapsack_a.used_weight() <= self.instance.capacity_1)
self.model.add(self._knapsack_b.used_weight() <= self.instance.capacity_2)
self.model.add(self._knapsack_a.used_weight() + self._knapsack_b.used_weight() <= self.instance.capacity_total)
# Add a constraint that items cannot be packed in both knapsacks
for i in range(len(instance.weights)):
self.model.add_at_most_one(self._knapsack_a.packs_item(i), self._knapsack_b.packs_item(i))
def _add_objective(self):
self.model.maximize(self._knapsack_a.packed_value() + self._knapsack_b.packed_value())
 Do not create such a container class for simple models where the container would only wrap a list or a dictionary without adding any additional functionality. In such cases, directly using the list or dictionary is preferable, as it is more concise and easier to understand. The same is true for individual variables that do not need a container at all. |
Lazy Variable Construction
In models with numerous auxiliary variables, often only a subset is actually used by the constraints. Attempting to create only the variables that are needed can require complex code to ensure that exactly the right variables are generated. If the model is extended later, this process becomes even more complicated, as you may not know upfront which variables will be needed. This is where lazy variable construction comes into play. By creating variables only when they are accessed, we ensure that only necessary variables are generated, reducing memory usage and computational overhead. While this approach might be more expensive if most variables end up being used anyway, it can save significant resources when only a small subset is actually needed.
To illustrate this concept, we introduce the _CombiVariables class. This class
manages auxiliary variables that indicate when a pair of items is packed
together, allowing us to assign additional bonuses for packing certain items
together. Theoretically, the number of possible item combinations is quadratic
in the number of items, but in practice, only a few may be relevant. By creating
these variables lazily—only when they are accessed—we reduce memory usage and
computational overhead.
class _CombiVariables:
def __init__(
self,
instance: KnapsackInstance,
model: cp_model.CpModel,
item_vars: _ItemSelectionVars,
):
self.instance = instance
self.model = model
self.item_vars = item_vars
self.bonus_vars = {}
def __getitem__(self, item_pair: Tuple[int, int]) -> cp_model.IntVar:
i, j = sorted(item_pair)
if (i, j) not in self.bonus_vars:
var = self.model.NewBoolVar(f"bonus_{i}_{j}")
self.model.add(
self.item_vars.packs_item(i) + self.item_vars.packs_item(j) >= 2 * var
)
self.bonus_vars[(i, j)] = var
return self.bonus_vars[(i, j)]
In the KnapsackSolver, we can now treat these variables as if they were all
pre-created, without worrying about the underlying optimization. Note that we
have moved the creation of the objective function into the solve method, as
adding bonuses for item combinations will modify the objective function. Also,
by encapsulating item variables into a separate class (_ItemSelectionVars), we
can easily pass them around and use them in other components.
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self._item_vars = _ItemSelectionVars(instance, self.model)
self._bonus_vars = _CombiVariables(instance, self.model, self._item_vars)
self._objective_terms = [self._item_vars.packed_value()] # Initial objective terms
self.solver = cp_model.CpSolver()
def solve(self) -> KnapsackSolution:
self.model.maximize(sum(self._objective_terms))
self.solver.parameters.max_time_in_seconds = self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=self._item_vars.extract_packed_items(self.solver),
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def add_bonus(self, item_a: int, item_b: int, bonus: int):
bonus_var = self._bonus_vars[(item_a, item_b)]
self._objective_terms.append(bonus * bonus_var)
 If we are sure to only call |
Submodels
We can further enhance our modeling approach by encapsulating entire sections of the model—not just individual variables—into separate submodels. This technique is particularly useful for complex models where different components are loosely connected. By partitioning the model into smaller, more manageable submodels, we improve modularity and maintainability. Submodels communicate with the main model through shared variables, effectively hiding internal details like auxiliary variables. If requirements change, we can often reconfigure or replace specific submodels without affecting the rest of the model. In larger contexts, it is also common for logic to repeat in different optimization problems of the system, so building a collection of submodels allows us to quickly assemble new models using reusable components.
For instance, piecewise linear functions can be modeled as submodels, as
demonstrated with the PiecewiseLinearConstraint class in
piecewise_linear_function.py.
Each submodel handles a piecewise linear function independently, interfacing
with the main model through shared x and y variables. By encapsulating the
logic for each piecewise function in a dedicated class, we make it reusable and
testable in isolation.
from ortools.sat.python import cp_model
requirements_1 = (3, 5, 2)
requirements_2 = (2, 1, 3)
model = cp_model.CpModel()
buy_1 = model.new_int_var(0, 1_500, "buy_1")
buy_2 = model.new_int_var(0, 1_500, "buy_2")
buy_3 = model.new_int_var(0, 1_500, "buy_3")
produce_1 = model.new_int_var(0, 300, "produce_1")
produce_2 = model.new_int_var(0, 300, "produce_2")
model.add(produce_1 * requirements_1[0] + produce_2 * requirements_2[0] <= buy_1)
model.add(produce_1 * requirements_1[1] + produce_2 * requirements_2[1] <= buy_2)
model.add(produce_1 * requirements_1[2] + produce_2 * requirements_2[2] <= buy_3)
# You can find the PiecewiseLinearFunction and PiecewiseLinearConstraint classes in the utils directory
from piecewise_functions import PiecewiseLinearFunction, PiecewiseLinearConstraint
# Define the functions for the costs
costs_1 = [(0, 0), (1000, 400), (1500, 1300)]
costs_2 = [(0, 0), (300, 300), (700, 500), (1200, 600), (1500, 1100)]
costs_3 = [(0, 0), (200, 400), (500, 700), (1000, 900), (1500, 1500)]
f_costs_1 = PiecewiseLinearFunction(
xs=[x for x, y in costs_1], ys=[y for x, y in costs_1]
)
f_costs_2 = PiecewiseLinearFunction(
xs=[x for x, y in costs_2], ys=[y for x, y in costs_2]
)
f_costs_3 = PiecewiseLinearFunction(
xs=[x for x, y in costs_3], ys=[y for x, y in costs_3]
)
# Define the functions for the gains
gain_1 = [(0, 0), (100, 800), (200, 1600), (300, 2000)]
gain_2 = [(0, 0), (80, 1000), (150, 1300), (200, 1400), (300, 1500)]
f_gain_1 = PiecewiseLinearFunction(
xs=[x for x, y in gain_1], ys=[y for x, y in gain_1]
)
f_gain_2 = PiecewiseLinearFunction(
xs=[x for x, y in gain_2], ys=[y for x, y in gain_2]
)
# Create y >= f(x) constraints for the costs
x_costs_1 = PiecewiseLinearConstraint(model, buy_1, f_costs_1, upper_bound=False)
x_costs_2 = PiecewiseLinearConstraint(model, buy_2, f_costs_2, upper_bound=False)
x_costs_3 = PiecewiseLinearConstraint(model, buy_3, f_costs_3, upper_bound=False)
# Create y <= f(x) constraints for the gains
x_gain_1 = PiecewiseLinearConstraint(model, produce_1, f_gain_1, upper_bound=True)
x_gain_2 = PiecewiseLinearConstraint(model, produce_2, f_gain_2, upper_bound=True)
# Maximize the gains minus the costs
model.maximize(x_gain_1.y + x_gain_2.y - (x_costs_1.y + x_costs_2.y + x_costs_3.y))
Testing complex optimization models is often challenging because outputs can be sensitive to small changes in the model. Even with a good test case, detected errors may be difficult to trace. By extracting elements into submodels, you can test these submodels independently, ensuring they work correctly before integrating them into the main model.
Submodels are usually much simpler than the overall problem, making them easy to optimize and, thus, fast to test their optimal solution.
from ortools.sat.python import cp_model
def test_piecewise_linear_upper_bound_constraint():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
# Using the submodel
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
model.maximize(c.y)
# Checking its behavior
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.OPTIMAL
assert solver.value(c.y) == 10
assert solver.value(x) == 10
Alternatively, testing for feasibility or infeasibility can be a good choice, especially if the submodel does not directly correspond to an optimization problem on its own.
from ortools.sat.python import cp_model
def test_piecewise_linear_upper_bound_constraint_via_fixation():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
# Fix the variables to specific values
model.add(x == 10)
model.add(c.y == 10)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.OPTIMAL, "The model should be feasible"
def test_piecewise_linear_upper_bound_constraint_via_fixation_infeasible():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
# Fix the variables to specific values that violate the constraint
model.add(x == 10)
model.add(c.y == 11)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.INFEASIBLE, "The model should be infeasible"
Embedding CP-SAT in an Application via multiprocessing
If you want to embed CP-SAT in your application for potentially long-running optimization tasks, you can utilize callbacks to provide users with progress updates and potentially interrupt the process early. However, one issue is that the application can only react during the callback. Since the callback is not always called frequently, this may lead to problematic delays, making it unsuitable for graphical user interfaces (GUIs) or application programming interfaces (APIs).
An alternative is to let the solver run in a separate process and communicate with it using a pipe. This approach allows the solver to be interrupted at any time, enabling the application to react immediately. Python’s multiprocessing module provides reasonably simple ways to achieve this. This example showcases such an approach. However, for scaling this approach up, you will actually have to build a task queues where the solver is run by workers. Using multiprocessing can still be useful for the worker to remain responsive for stop signals while the solver is running.
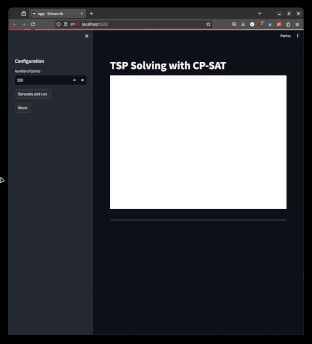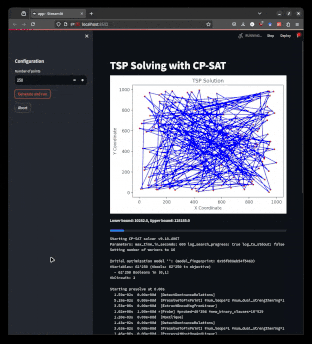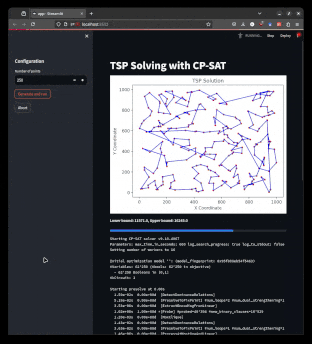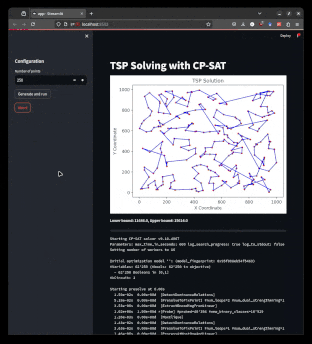 |
|---|
| Using multiprocessing, one can build a responsive interface for a solver. |
@oulianov deployed it here for you to try out in your browser.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Test-Driven Development with CP-SAT

In this chapter, we demonstrate how to apply test-driven development (TDD) principles to the nurse rostering problem using the CP-SAT solver. Our objective is to build a model that is modular, thoroughly tested, extensible, and straightforward to maintain.
I consider TDD a valuable approach for optimization problems, even though I do not follow the formal TDD cycle strictly. Writing tests early helps clarify requirements, refine problem specifications, and expose ambiguities in the initial formulation. In many real-world scenarios, the problem statement is incomplete or evolving. By expressing expectations as executable tests, we can communicate requirements more effectively and adjust them as new insights emerge.
The nurse rostering problem is particularly suitable for illustrating this approach. It represents a class of scheduling problems where constraints and objectives change frequently in response to stakeholder feedback. In such settings, modular design and systematic testing substantially reduce the cost of adapting and validating the model as requirements evolve.
For small or well-defined problems, a simple implementation with a few manual checks may suffice. However, as complexity grows and outcomes become harder to verify informally, a structured, test-driven approach proves highly beneficial. It allows the problem to be decomposed into smaller, testable components that can be incrementally implemented, validated, and refined.
This chapter does not advocate for perfection at the outset. In practice, building a working prototype often comes first, and design improvements are introduced once they offer clear benefits. The key is to maintain a balance between rapid prototyping and introducing structure and tests at the right stage of development.
We will incrementally construct a nurse rostering model using CP-SAT, guided by test-driven principles. The workflow includes defining formal data schemas for inputs and outputs, implementing solver-independent validation functions that encode constraints and objectives, and creating modular components for decision variables, constraints, and soft objectives. We conclude by combining these modules into a complete solver and verifying its solutions on test instances. However, before doing so, we will briefly review a classical approach and what can go wrong when the problem complexity increases.
 This chapter is not intended as a strict guideline but as one possible approach. I do not follow every step outlined here in every project. Instead, I aim to share principles that I have found useful in practice. Operations researchers may gain insights into software engineering practices, while software engineers may learn how to apply their skills to optimization models. Experienced optimizers may find value in comparing their own approach with the one presented here. |
|
There appears to be limited material addressing software engineering practices specifically in operations research. However, the talk Optimization Modeling: The Art of Not Making It an Art by Ronald van der Velden (Gurobi) is an excellent resource that partially overlaps with the themes discussed in this chapter. (Note: Registration with a company name and email address is required to access the content.)  |
You can find the complete code for this chapter here.
Classical Steps for Textbook Problems
Before introducing the more advanced TDD-inspired workflow, let us briefly review a classical approach to implementing optimization models, as commonly encountered in textbook exercises or university homework. This traditional approach can also be effective for many real-world problems, provided their complexity remains moderate. However, real-world problems often introduce additional challenges that are absent from well-structured academic exercises. As the problem complexity increases, this classical approach becomes difficult to manage. We will therefore explore how software engineering practices can help address these challenges.
Let us consider a concrete example: the Facility Location Problem (FLP). To set the right context, we will present it as if it were stated directly on a homework sheet:
A delivery company is planning to open new warehouses to serve its customers. There is a set \( F \) of potential warehouse locations, and a set \( C \) of customers who need to receive their orders.
Opening a warehouse at location \( i \in F \) comes with a fixed cost \( f_i \). Shipping goods from warehouse \( i \in F \) to customer \( j \in C \) costs \( c_{i,j} \).
Every customer \( j \in C \) must be served by exactly one warehouse, and a warehouse can only ship goods if it is actually opened.
The company needs to decide which warehouse locations \( i \in F \) to open and which warehouse will serve each customer \( j \in C \) so that the total cost—consisting of the opening costs \( f_i \) and the shipping costs \( c_{i,j} \)—is as small as possible.
Now, a good idea would be to highlight parameters, decisions, constraints, and objectives in the text (using different colors), and then write down the mathematical formulation of the problem in the following steps:
- Parameters: Define the problem parameters, specifying the input data for the model.
- Decision Variables: Define the variables representing the decisions or assignments to be made.
- Constraints and Objectives: Specify the constraints that must be satisfied and the objectives to be optimized.
For this problem, this would look like this:
Parameters:
- \( F \): Set of potential facility locations.
- \( C \): Set of customers.
- \( f_i \in \mathbb{N}_0 \) for \( i \in F \): Fixed cost of opening facility \( i \).
- \( c_{i,j} \in \mathbb{N}_0 \) for \( i \in F, j \in C \): Cost of serving customer \( j \) from facility \( i \).
Decision Variables:
- \( y_i \in \mathbb{B} \ \forall i \in F \): \( y_i = 1 \) if facility \( i \) is opened, and 0 otherwise.
- \( x_{i,j} \in \mathbb{B} \ \forall i \in F, j \in C \): \( x_{i,j} = 1 \) if customer \( j \) is served by facility \( i \), and 0 otherwise.
Objective Function:
Minimize the total cost of opening facilities and serving customers: \( \min \sum_{i \in F} f_i \cdot y_i + \sum_{i \in F} \sum_{j \in C} c_{i,j} \cdot x_{i,j}. \)
Constraints:
- Customer Assignment: Each customer must be served by exactly one open facility: \( \sum_{i \in F} x_{i,j} = 1 \quad \forall j \in C. \)
- Facility Activation: A customer can only be served by a facility if that facility is open: \( x_{i,j} \leq y_i \quad \forall i \in F, j \in C. \)
The mathematical notation is so compact that one can easily work through it on a whiteboard or a sheet of paper, which makes it ideal for group discussions. Such concise, precise notation also makes it easier to identify inconsistencies or errors directly at least for smaller problems.
Finally, you implement it either with your favorite optimization framework or modelling language. In case of an exercise, it is also very likely that your instructor has already provided some test instances, which you can use to verify your implementation.
from ortools.sat.python import cp_model
# 1. Parameters
F = [1, 2, 3] # Set of potential facility locations.
C = [1, 2, 3] # Set of customers.
f = {1: 100, 2: 200, 3: 150} # Fixed cost f[i] of opening facility i.
c = {1: {1: 10, 2: 20, 3: 30},
2: {1: 15, 2: 25, 3: 35},
3: {1: 20, 2: 30, 3: 40}} # Cost c[i][j] of serving customer j from facility i.
model = cp_model.CpModel()
# 2. Decision variables
y = {i: model.new_bool_var(f'y_{i}') for i in F} # y[i] = 1 if facility i is opened.
x = {(i, j): model.new_bool_var(f'x_{i}_{j}') for i in F for j in C} # x[i,j] = 1 if customer j is served by facility i.
# 3. Objective function
model.minimize(
sum(f[i] * y[i] for i in F) + sum(c[i][j] * x[i, j] for i in F for j in C)
)
# 4. Constraints
for j in C:
model.add(sum(x[i, j] for i in F) == 1) # Each customer must be served by exactly one open facility.
for i in F:
for j in C:
model.add(x[i, j] <= y[i]) # A customer can only be served by a facility if that facility is open.
# Solve the model
solver = cp_model.CpSolver()
status = solver.solve(model)
# ...
Usually you would implement this in a function; however, I often need to make models incremental, which is not compatible with stateless functions. Moreover, using classes in Python is almost as straightforward as using pure functions. Being able to manipulate the model after construction, like fixing certain variables, also makes it easier to test and debug.
I would encapsulate this code in a class to enhance reusability, resulting in an implementation similar to the following:
class FacilityLocationModel:
def __init__(self, F, C, f, c):
self.F, self.C, self.f, self.c = F, C, f, c
self.model = cp_model.CpModel()
# 2. Decision variables
self.y = {i: self.model.new_bool_var(f'y_{i}') for i in self.F} # y[i] = 1 if facility i is opened.
# ...
def solve(self, **parameters):
# Solve the model
solver = cp_model.CpSolver()
# ...
As you can see, the implementation is actually nearly identical to the mathematical formulation and many experts may opt to directly implement it, especially when using modeling languages like Pyomo, GAMS, or AMPL.
In practice, many cases are still simple enough to follow this workflow. Although the data may not be readily available or may require extensive preprocessing, and the problem statement may not yet be fully defined, it is often possible to sketch the mathematical formulation and then implement it in a single step. This is particularly feasible because many problems are essentially well-known combinatorial optimization problems, merely obscured by domain-specific terminology. With experience, you can often identify the underlying structure of the problem quickly and adapt them to custom constraints with ease.
As long as the model remains this simple, you may only need to add a few basic tests to verify that the solutions behave as expected; there is no need for modularization or extensive validation functions. Such a model is easy to understand and can be implemented within minutes. It can be presented on a single slide, and any additional structure would likely introduce unnecessary complexity rather than improving clarity.
Mathematical abstraction can simplify a problem; however, it can also become so abstract that the original problem is no longer recognizable. While the threshold varies depending on one’s background, there comes a point at which monolithic mathematical formulations become incomprehensible, and even minor modifications require significant effort. It will also be extremely difficult to debug such a model if you cannot look at components in isolation. This situation parallels a software architecture that, while initially straightforward, has accumulated complexity through incremental growth, to the point where any modification is fraught with risk and development velocity suffers.
Here are a few things that can go wrong when the model grows too complex:
- You are the only one who understands the model, making it unmaintainable by others.
- Even you no longer fully understand the model, causing simple changes to take forever or to break things—often only discovered when it fails in production.
- The model’s complexity makes it impossible to verify individual components in isolation, making root-cause analysis extremely difficult.
- Testing becomes impractical, leaving you with constant doubts about whether the model is correct.
- A subtle bug silently excludes high-quality solutions, leading to significant opportunity loss without any explicit error.
- Bad or inconsistent data goes undetected due to missing validation checks, producing incorrect results and eroding trust in your code.
- Communication with stakeholders breaks down because you lack a clear, shared language to formally specify requirements.
- The model becomes so convoluted that implementing all requirements—or even building a first useful prototype—feels impossible.
- No clear input/output data interfaces, making collaboration and integration difficult.
- …
All of these issues may fail the project, before even reaching the real challenges of optimizing scalability and ensuring real-world accuracy.
In the remainder of this chapter, we will explore how to avoid this situation by applying software engineering practices to optimization models on the example of the nurse rostering problem. We will do the following steps:
- Data Schema: Define structured schemas for the problem instance and solution, covering parameters and parts of the decision space.
- Validation Functions: Implement functions to verify feasibility and compute objective values, serving as the formal specification.
- Decision Variables: Introduce decision variables encapsulated in containers to simplify constraint and objective construction.
- Modular Constraints and Objectives: Build constraints and soft objectives as independent, testable modules.
- Solver Integration: Combine these components into a complete CP-SAT model and test it in completion to check that the components work together as expected.
 You can transition fluently between the two approaches; it is not an all-or-nothing choice. It is entirely feasible to adopt only parts of the approach described here and apply them to selected aspects of the problem. |
The Nurse Rostering Problem
Before implementing a solution, we first outline the nurse rostering problem and its initial requirements. The nurse rostering problem involves assigning a set of nurses to shifts over a defined planning horizon. Each shift has a specified demand indicating the minimum number of nurses required. The goal is to produce an assignment that satisfies all operational constraints while optimizing soft preferences and priorities. In this example, the requirements are as follows:
Constraints (Hard Requirements):
- Unavailability Constraint: A nurse must not be assigned to any shift for which they are unavailable or explicitly blocked.
- Shift Coverage Requirement: Each shift must be staffed with a sufficient number of nurses to meet its demand.
- Rest Period Constraint: A nurse must have an adequate rest period between consecutive shifts. If the interval between the end of one shift and the start of the next is too short, the nurse cannot be assigned to both.
Objectives (Soft Goals):
- Preference Satisfaction: Nurses may indicate preferences for particular shifts. The model should honor these preferences wherever possible.
- Staffing Preference: Internal staff members should be preferred over external or contract nurses when all other constraints are satisfied.
To keep the initial formulation manageable, we start with this limited set of constraints and objectives. The implementation is designed to be modular and extensible, allowing additional requirements—such as fairness, seniority, on-call shifts, and others—to be introduced later with minimal refactoring. While the initial requirements may still be easily implemented in a monolithic model, it should already be complex enough to illustrate the benefits of a more structured, test-driven approach.
 This chapter focuses on correctness, not performance. First, ensure the solution is correct; only then focus on making it efficient. Correspondingly, the implementation here may not be the most efficient. |
Instance and Solution Schema
In academic or textbook settings, one often starts with clean, well-structured data that is perfectly tailored to the problem at hand. In real-world projects, however, this is rarely the case. You are often lucky to receive any data at all—let alone data that is complete, consistent, and ready for use.
Data may not yet exist in digital form, or it may still be collected manually—perhaps even on paper. Even if a digital system is under development, it may not yet be deployed, and any available data might be outdated or incomplete. Privacy concerns or legal constraints may further restrict access to critical information, especially when working with personnel data, such as nurse schedules.
 Obtain a data sample as early as possible, even if it is only an “educated guess” or a small subset of the actual dataset. Such samples simplify the extraction of test cases and support iterative discussions with stakeholders, who often overlook trivial but important details. For instance, the model developed here does not enforce a single shift per day, focusing instead on rest periods and total working hours over a given period (e.g., a week). Stakeholders are likely to recognize such omissions as soon as they review a solution for a realistic instance. Addressing these issues typically requires an agile, iterative process, which we omit here for simplicity but which can be applied throughout all phases of this example. |
And when the data does arrive, it often brings problems of its own. It may be incomplete, contain contradictory entries, or be structured inconsistently. Excel remains a de facto standard in many organizations, which introduces risks such as data type mismatches, inconsistent formatting, or broken formulas. Even worse are schemaless databases like Firestore, which offer no guarantees about the structure or consistency of stored documents. It is not uncommon to find fields that sometimes contain integers, sometimes strings, and occasionally just vanish altogether—along with keys that are misspelled, duplicated, or silently dropped.
In such environments, any error in the data will propagate directly to your application. Your logic fails not because your model is incorrect, but because upstream inputs violate assumptions you did not realize you were making.
After enough frustrating encounters with malformed data, I became a strong proponent of defining formal data schemas as a first step in any serious optimization project. For Python, I have found Pydantic to be an excellent tool: it allows you to define input and output schemas declaratively, enforces type checks and invariants automatically, and raises clear validation errors when assumptions are violated. With these schemas in place, problems can be caught early and diagnosed easily—long before they produce incorrect results or puzzling failures.
Defining a schema is also crucial for ensuring that all collaborators (including clients) are aligned in their understanding of the problem. You may all be using the same terms—like “shift”, “start time”, or “duration”—but interpret them differently. Is that duration in seconds, minutes, or hours? Is the “shift ID” an index or a foreign key to a separate table? Without a precise schema, it is easy to make dangerous assumptions.
A vivid historical example is the loss of the Mars Climate Orbiter in 1999. The spacecraft was destroyed because one team used imperial units while another expected metric, and there was no enforced contract between the systems. The entire $327 million mission failed because of a silent mismatch in a shared data interface. While most optimization projects are not launching spacecraft, the takeaway is just as relevant: never assume shared understanding—make your assumptions explicit.
That is why I prefer to define and document both the input and output schemas at the beginning of a project, even before writing the first line of algorithmic code. It helps formalize the problem, clarifies the roles of different fields, and allows everyone to work toward the same structure. Even if the schema evolves over time (and it almost certainly will), the evolution is transparent, versioned, and easy to manage.
Below is the data schema we will be using for the nurse rostering problem. We
made two non-trivial additions: preferred_shift_weight and staff_weight.
These will unlikely be part of the initial problem formulation, but as we have
two objectives, this would allow us to easily weight the two objectives against
each other. It could be that later on, we decide that the optimization should be
lexicographic, making these weights irrelevant, but it is a good starting point
to have at least some way of balancing the two objectives. If there are more
parameters to specify the problem, e.g., switching constraints on and off, I
would create a separate NurseRosteringParameters class that contains these
parameters, instead of integrating them into the instance schema, but let us
skip that for simplicity.
"""
This module defines the data schema for the nurse rostering problem.
Note that this is just a random variant of the nurse rostering problem.
We define the instance and solution data structures using Pydantic.
"""
from datetime import datetime, timedelta
from pydantic import BaseModel, Field, NonNegativeInt, model_validator, PositiveInt
import uuid
# Semantic type aliases for clarity
NurseUid = int
ShiftUid = int
def generate_random_uid() -> int:
# Use uuid4 and convert to an integer (truncated to 64 bits for practical use)
return uuid.uuid4().int >> 64
class Nurse(BaseModel):
"""
Represents a nurse whose shifts we want to plan. Will be part of `NurseRosteringInstance`.
"""
uid: NurseUid = Field(
default_factory=generate_random_uid,
description="Unique identifier for the nurse",
)
name: str = Field(..., description="Name of the nurse")
preferred_shifts: set[ShiftUid] = Field(
..., description="List of preferred shift UIDs for the nurse"
)
blocked_shifts: set[ShiftUid] = Field(
..., description="List of blocked shift UIDs for the nurse"
)
staff: bool = Field(
...,
description="Indicates if the nurse is a staff member (True) or a contractor (False)",
)
min_time_between_shifts: timedelta = Field(
..., description="Minimum off duty time between two shifts for the same nurse"
)
preferred_shift_weight: NonNegativeInt = Field(
default=1,
description="The weight in the objective function for every assigned preference.",
)
class Shift(BaseModel):
"""
Represents a shift that needs to be covered by nurses. Will be part of `NurseRosteringInstance`.
"""
uid: ShiftUid = Field(
default_factory=generate_random_uid,
description="Unique identifier for the shift",
)
name: str = Field(..., description="Name of the shift (e.g., '2025-01-01 Morning')")
start_time: datetime = Field(
..., description="Start time of the shift as a full datetime (YYYY-MM-DD HH:MM)"
)
end_time: datetime = Field(..., description="End time of the shift as a full datetime (YYYY-MM-DD HH:MM)")
demand: NonNegativeInt = Field(
..., description="Number of nurses required for this shift"
)
class NurseRosteringInstance(BaseModel):
"""
This schema defines the INPUT for the nurse rostering problem.
"""
nurses: list[Nurse] = Field(
..., description="List of nurses in the rostering instance"
)
shifts: list[Shift] = Field(
...,
description="List of shifts that need to be covered. Shifts must be sorted in time.",
)
staff_weight: int = Field(
default=1,
description="The weight in the objective function for each assigned staff nurse.",
)
@model_validator(mode="after")
def validate_shifts_unique_uids(self):
"""
Ensure that all shifts have unique UIDs to avoid conflicts.
"""
shift_uids = {shift.uid for shift in self.shifts}
if len(shift_uids) != len(self.shifts):
raise ValueError("Shift UIDs must be unique.")
return self
@model_validator(mode="after")
def validate_nurses_unique_uids(self):
"""
Ensure that all nurses have unique UIDs to avoid conflicts.
"""
nurse_uids = {nurse.uid for nurse in self.nurses}
if len(nurse_uids) != len(self.nurses):
raise ValueError("Nurse UIDs must be unique.")
return self
@model_validator(mode="after")
def validate_shifts_sorted_by_time(self):
"""
Ensure that shifts are sorted by start time.
"""
for shift_a, shift_b in zip(self.shifts, self.shifts[1:]):
if shift_a.start_time > shift_b.start_time:
raise ValueError("Shifts must be sorted by start time.")
return self
For the solution, each shift is mapped to a list of assigned nurses. In
addition, the objective value and the timestamp at which the solution was
computed are recorded. As a potential improvement, the list[NurseUid]
structure could be replaced with a dedicated Pydantic model. This approach would
allow for the inclusion of additional shift-specific data in the future, which
cannot be directly attached to a plain list. Such a design would be
particularly advantageous when the solution must be presented in a user
interface. Nevertheless, as long as the base object is defined as a Pydantic
model, it is generally possible to maintain backward compatibility when
extending the schema, even when certain native Python elements are involved.
class NurseRosteringSolution(BaseModel):
"""
This schema defines the OUTPUT for the nurse rostering problem.
"""
nurses_at_shifts: dict[ShiftUid, list[NurseUid]] = Field(
..., description="Maps shift UIDs to lists of assigned nurse UIDs."
)
objective_value: int = Field(
description="Objective value of the computed solution."
)
timestamp: datetime = Field(
default_factory=datetime.now,
description="Time when the solution was generated. Takes little space and can be extremely useful when investigating issues with the solution. Optimally, also add the revision of the algorithm that generated the solution, e.g., by using a git commit hash.",
)
# Validation of the solution will be handled in a separate module.
With these schemas in place, it becomes immediately clear what structure the
input and output must follow. The model_validator methods let you encode
important assumptions—such as uniqueness or sorting—and they raise explicit
errors if those assumptions are violated. While this does not guarantee that all
data is actually correct, it prevents many accidental errors and makes debugging
significantly easier. By catching issues at the boundary, you gain confidence
that the optimization logic operates on well-formed inputs.
 You do not need to use the same schema for the endpoint contract and the internal representation of the optimization model. Converting between different schemas is inexpensive compared to the computational cost of solving the model. If a different representation enables more efficient model construction, introduce an additional layer. Remember that the internal schema can be modified easily, but changes to the outward-facing schema must be handled carefully to avoid breaking existing interfaces. |
Tabular Data
Many people, including myself, appreciate working with tables. In the chapter’s example project, we use a nested data structure. However, in many projects tabular data is entirely sufficient, and in such cases you should prefer this representation. In principle, any data structure can be expressed in tabular form, and most common databases, in particular relational databases accessed via SQL, are built around tables. Nevertheless, when extracting information requires complex joins or aggregations, you may need to either restructure your tables or adopt a more object-oriented format, for example by using Pydantic models as shown above. Since input data should not be modified during model construction, it is perfectly acceptable to employ both representations in parallel.
If your data can be naturally and intuitively expressed in tabular form, then you should retain this representation. Python provides excellent libraries for working with tabular data, most notably Pandas and Polars. Pandas is the most widely used library for data analysis in Python, and it benefits from a rich ecosystem of extensions and integrations. However, it can exhibit performance limitations, particularly with large datasets. Polars is a newer library that is more performance-oriented. Since optimization problems typically involve much smaller datasets than those encountered in data analysis or machine learning, the widespread use and ecosystem of Pandas usually make it the more suitable choice.
The major advantage of storing data in a Pandas DataFrame is the ability to perform aggregations, filtering, and transformations with a concise and expressive syntax. In addition, Pandas integrates well with visualization libraries such as Matplotlib and Seaborn, which allow you to easily create informative visual representations of your data.
Do you want to scale a column to the range [0, 1]? This requires only a single line of code:
df['scaled_column'] = (df['column'] - df['column'].min()) / (df['column'].max() - df['column'].min())
Do you want to filter rows based on a condition? Again, this can be achieved in one line:
filtered_df = df[df['column'] > threshold]
CP-SAT also provides integration with Pandas, as demonstrated in the following
knapsack example, where the values and weights of items are stored in a
DataFrame:
from ortools.sat.python import cp_model
import pandas as pd
# Example data: each row is an item with a weight and a value
# In production, you would likely load this from a file or database,
# which pandas has simple loaders for.
df = pd.DataFrame(
data={
"weight": [2, 4, 3, 5, 1, 6, 2, 7, 3, 4],
"value": [10, 8, 7, 6, 5, 9, 4, 3, 2, 1],
},
index=["A", "B", "C", "D", "E", "F", "G", "H", "I", "J"],
)
model = cp_model.CpModel()
# Create a Boolean variable for each item (indexed by DataFrame index)
x = model.new_bool_var_series("x", df.index)
# Use Pandas vectorized operations to build constraints and objectives
model.add((x @ df["weight"]) <= 15) # total weight limit
model.maximize(x @ df["value"]) # maximize total value
Some constraints can also be conveniently added row by row. For example, suppose we have a set of prohibited pairs of items that cannot be selected together. Such restrictions can be represented naturally as a two-column table:
prohibited_pairs_df = pd.DataFrame(
data={
"item1": ["A", "B", "C"],
"item2": ["D", "E", "F"],
}
)
# For each row, apply the corresponding constraint
for _, row in prohibited_pairs_df.iterrows():
model.add(x[row["item1"]] + x[row["item2"]] <= 1)
Suppose we have not only prohibited pairs of items but arbitrary sets of items that cannot be selected together. To express this structure in a classical tabular format, we would introduce a unique identifier for each set and a relation table that maps item identifiers to set identifiers. To build the constraints, we would first group the rows by set identifier, aggregate the corresponding item identifiers, and then add the constraint for each set. If this requirement constitutes only a small portion of the model, the tabular approach is acceptable. However, if the model relies on many such sets or lists, I recommend switching to a more object-oriented representation, as used in the nurse rostering problem in this chapter.
When working with tabular data, it is still important to enforce a strict schema, as we did with the Pydantic models above. This can be achieved with libraries such as pandera. For instance, we can require that the weights and values of the items are non-negative integers. Although this may appear trivial, errors can easily arise, for example when data is extracted from widely used Excel files somewhere in the processing pipeline.
import pandas as pd
import pandera.pandas as pa
schema = pa.DataFrameSchema({
"weight": pa.Column(int, pa.Check.ge(0)),
"value": pa.Column(int, pa.Check.ge(0)),
})
validated_df = schema.validate(df)
 Princeton Consultants provide an excellent post on Rapid Optimization Model Development with Python and pandas in 7 Steps, which offers a more detailed discussion of the model-building process with Pandas. In my own work, I am often involved in projects where the data is more graph-like or hierarchical, in which case Pydantic tends to be a more natural representation for building optimization models. I explicitly added this subsection to emphasize that using nested data with Pydantic is not the only approach, and it is not always the best one. Ultimately, you should choose the representation that best matches your data and your team. If necessary, use multiple representations in parallel, as the additional memory overhead is usually negligible. |
Solver-Agnostic Validation
With the data schemas defined, we can now implement validation functions that check whether a proposed solution satisfies all constraints. This is the first concrete step toward a test-driven workflow.
These validation functions are solver-independent, meaning they do not rely on any specific algorithm or library like CP-SAT. This makes them ideal for communicating and verifying the specification with domain experts or clients. In fact, someone with only basic programming skills could review or even contribute to these checks, reducing misunderstandings about the problem’s requirements.
In addition to feasibility, we also define the objective function here. That might seem unusual for validation logic, but it provides a clear and unambiguous specification of what we are trying to optimize. In practice, the objective function is often the most volatile part of the specification—frequently revised as new goals, costs, or incentives are introduced. By expressing it in code, we make it easier to reason about and iterate on collaboratively.
 Crafting an effective objective function requires experience. I have often observed less experienced practitioners reaching incorrect conclusions about its proper formulation. Common errors include unintentionally encoding parts of the objective as constraints or defining the objective in a way that allows undesirable trade-offs between its components. If a client provides an objective function, do not implement it blindly; instead, analyze it carefully before proceeding. |
By writing these checks up front, we make the problem precise and executable. Even without an optimization engine, we already know how to distinguish valid from invalid solutions and how to compare two feasible solutions in terms of quality. This gives us a solid foundation for developing and testing optimization algorithms in the next steps. If we are lucky, we could even use it as a feedback loop for an AI assistant to code the solution for us, although my experiences with that have been mixed so far.
The following Python module provides these validation checks and a function to compute the objective value:
"""
This module contains validation functions for nurse rostering solutions.
It is solver and algorithm agnostic, meaning it can be used to validate solutions
from any solver that produces a `NurseRosteringSolution` object. Just by providing
such functions, you have taken a huge step toward computing a solution, as you now
have a clean specification of what a valid and good solution looks like.
"""
from collections import defaultdict
from .data_schema import NurseRosteringInstance, NurseRosteringSolution
def assert_consistent_uids(
instance: NurseRosteringInstance, solution: NurseRosteringSolution
):
"""
Assert that all UIDs in the solution are part of the instance.
"""
nurse_uids = {n.uid for n in instance.nurses}
shift_uids = {s.uid for s in instance.shifts}
for shift_uid, nurse_list in solution.nurses_at_shifts.items():
if shift_uid not in shift_uids:
raise AssertionError(f"Shift {shift_uid} is not present in the instance.")
for nurse_uid in nurse_list:
if nurse_uid not in nurse_uids:
raise AssertionError(
f"Nurse {nurse_uid} is not present in the instance."
)
def assert_no_blocked_shifts(
instance: NurseRosteringInstance, solution: NurseRosteringSolution
):
"""
Assert that no nurse is assigned to a blocked shift in the solution.
"""
for nurse in instance.nurses:
for shift_uid in nurse.blocked_shifts:
if (
shift_uid in solution.nurses_at_shifts
and nurse.uid in solution.nurses_at_shifts[shift_uid]
):
raise AssertionError(
f"Nurse {nurse.uid} is assigned to blocked shift {shift_uid}."
)
def assert_demand_satisfaction(
instance: NurseRosteringInstance, solution: NurseRosteringSolution
):
"""
Assert that each shift meets its nurse demand.
"""
for shift in instance.shifts:
assigned = solution.nurses_at_shifts.get(shift.uid, [])
if len(assigned) < shift.demand:
raise AssertionError(
f"Shift {shift.uid} demand not met: {len(assigned)}/{shift.demand} assigned."
)
def assert_min_time_between_shifts(
instance: NurseRosteringInstance, solution: NurseRosteringSolution
):
"""
Assert that nurses are not assigned to shifts too close together.
"""
shifts_by_uid = {s.uid: s for s in instance.shifts}
nurse_to_shifts = defaultdict(list)
for shift_uid, nurse_uids in solution.nurses_at_shifts.items():
for nurse_uid in nurse_uids:
nurse_to_shifts[nurse_uid].append(shifts_by_uid[shift_uid])
for nurse in instance.nurses:
assigned = sorted(nurse_to_shifts[nurse.uid], key=lambda s: s.start_time)
for a, b in zip(assigned, assigned[1:]):
if b.start_time < a.end_time + nurse.min_time_between_shifts:
raise AssertionError(
f"Nurse {nurse.uid} assigned to shifts {a.uid} and {b.uid} with insufficient rest."
)
def objective_value(
instance: NurseRosteringInstance, solution: NurseRosteringSolution
) -> int:
"""
Calculate the objective value of the solution based on the instance's preferences and staff assignments.
"""
nurses_by_uid = {n.uid: n for n in instance.nurses}
obj_val = 0
for shift_uid, nurse_uids in solution.nurses_at_shifts.items():
for nurse_uid in nurse_uids:
nurse = nurses_by_uid[nurse_uid]
if shift_uid in nurse.preferred_shifts:
# Preferred shifts decrease the objective (we minimize).
obj_val -= nurse.preferred_shift_weight
if not nurse.staff:
# Non-staff nurses incur a penalty (they are more expensive).
obj_val += instance.staff_weight
return obj_val
def assert_solution_is_feasible(
instance: NurseRosteringInstance,
solution: NurseRosteringSolution,
check_objective: bool = True,
):
"""
Run all standard feasibility checks.
"""
assert_consistent_uids(instance, solution)
assert_no_blocked_shifts(instance, solution)
assert_demand_satisfaction(instance, solution)
assert_min_time_between_shifts(instance, solution)
if check_objective:
obj_val = objective_value(instance, solution)
if obj_val != solution.objective_value:
raise AssertionError(
f"Objective value mismatch: expected {obj_val}, got {solution.objective_value}."
)
The main advantage of these validation functions is that they are completely independent of any solver or optimization model. This means we do not need to optimize their performance—they are meant to be correct, clear, and easy to understand. Precise and informative error messages are essential, as these will guide you when tests fail.
For simple problems, this level of validation may appear excessive, especially since CP-SAT already uses a declarative modeling style. However, these functions provide an independent specification of the problem, which is valuable for catching misunderstandings and hidden assumptions early.
For more complex problems, these validation functions are often simpler and more intuitive than the corresponding CP-SAT constraints. For example, when enforcing minimum rest times between shifts, the validation logic directly checks for violations, whereas CP-SAT encodes permissible patterns of assignments. In that sense, validation and CP-SAT complement each other: one detects what is wrong, the other defines what is allowed.
Lastly, it is quite possible that a pure CP-SAT model will not scale sufficiently, despite all optimizations and you will have to decompose the problem. These validation functions would remain useful and safeguard you while, e.g., replacing the vanilla CP-SAT model with a large neighborhood search or a metaheuristic approach.
 You could also add unit tests for these validation functions to ensure that they raise the expected errors for invalid inputs. However, I would consider this unnecessary in most cases, as the complementary nature of validation functions and CP-SAT constraints will likely catch most inconsistencies. If a test fails, always verify whether the test itself might be incorrect. |
Decision Variables
Up to this point, we have defined the parameters of the problem (through our Pydantic schemas) and created validation functions that serve as a solver-independent specification of the constraints and objectives. These validation functions essentially describe what a valid solution must look like and how we measure its quality.
The next step is to turn this high-level specification into a formal optimization model using CP-SAT. To do so, we start by defining decision variables, which represent the core choices of our problem. For the nurse rostering problem, a natural decision variable is:
Is nurse \( i \) assigned to shift \( j \)?
This can be represented by a Boolean variable \( x_{i,j} \) that is true if nurse \( i \) works shift \( j \), and false otherwise.
Instead of managing these variables as a raw two-dimensional array, we structure them using variable containers. For each nurse, we create a container that holds their assignment variables and provides useful methods for counting shifts, iterating over assignments, and extracting the solution. This approach keeps the model modular, makes constraints easier to implement, and supports reusability when we later add new constraints or objectives.
"""
This module provides a basic container to manage the variables for a single nurse in the nurse rostering problem.
"""
from collections.abc import Iterable
from ortools.sat.python import cp_model
from .data_schema import Nurse, Shift, ShiftUid
class NurseDecisionVars:
"""
A container to create and manage the decision variables for a single nurse.
Each nurse has one Boolean variable for each shift, indicating whether the nurse is assigned to that shift.
This class also provides helper methods to iterate over assignments and extract results.
"""
def __init__(self, nurse: Nurse, shifts: list[Shift], model: cp_model.CpModel):
self.nurse = nurse
self.shifts = shifts
self.model = model
# Create one Boolean decision variable per shift for this nurse
self._x = {
shift.uid: model.new_bool_var(f"assign_{nurse.uid}_{shift.uid}")
for shift in shifts
}
def fix(self, shift_uid: ShiftUid, value: bool):
"""
Fix the assignment variable for the given shift UID to a specific value (True or False).
Useful for setting hard constraints or testing the model.
"""
if shift_uid not in self._x:
raise ValueError(
f"Shift UID {shift_uid} not found in nurse {self.nurse.uid} assignments."
)
self.model.add(self._x[shift_uid] == value)
def is_assigned_to(self, shift_uid: ShiftUid) -> cp_model.BoolVarT:
"""
Return the decision variable for the given shift UID.
This variable is True if the nurse is assigned to that shift, and False otherwise.
"""
return self._x[shift_uid]
def iter_shifts(self) -> Iterable[tuple[Shift, cp_model.BoolVarT]]:
"""
Iterate over all (shift, variable) pairs for this nurse.
"""
for shift in self.shifts:
yield shift, self.is_assigned_to(shift_uid=shift.uid)
def extract(self, solver: cp_model.CpSolver) -> list[ShiftUid]:
"""
Extract a list of shift UIDs that this nurse is assigned to in the solution.
"""
return [shift_uid for shift_uid in self._x if solver.value(self._x[shift_uid])]
By encapsulating the decision variables in this manner, the process of
constructing constraints and objectives is simplified. Each constraint module
can focus on a single nurse or a subset of shifts without dealing with the
low-level details of variable creation or indexing. The behavior of the
NurseDecisionVars class can later be modified, for example, to avoid creating
variables for shifts irrelevant to a given nurse and instead return a constant
0 when such shifts are queried. These shifts can also be skipped in
iter_shifts to improve loop efficiency. Such refactoring is straightforward
with this container-based design but would be considerably more complex when
using, for instance, a raw two-dimensional array.
Modules
Now that we have defined the decision variables, the next step is to translate the problem constraints and objectives into an optimization model. For the nurse rostering problem, we have multiple constraints that are logically independent. Instead of writing them directly into a monolithic solver script, we will implement each constraint or objective as a separate module.
This modular approach offers several benefits:
- It keeps the model organized and readable.
- Each module can be tested individually (aligned with our TDD approach).
- Adding, removing, or modifying a constraint or objective later becomes trivial—simply add or replace a module.
To ensure all modules follow the same structure, we define an abstract base
class that specifies the interface for implementing constraints and
objectives. This base class defines a single method, build, which applies the
module’s constraints and optionally returns a sub-objective expression. These
sub-objectives will later be combined to form the global objective function.
The build method takes three arguments:
- The instance, which contains the problem parameters.
- The CP-SAT model, which we modify by adding constraints.
- A list of decision variable containers (one per nurse), which gives easy access to all variables related to that nurse.
Here is the abstract base class for all modules:
import abc
from ortools.sat.python import cp_model
from .data_schema import NurseRosteringInstance
from .nurse_vars import NurseDecisionVars
class ShiftAssignmentModule(abc.ABC):
@abc.abstractmethod
def build(
self,
instance: NurseRosteringInstance,
model: cp_model.CpModel,
nurse_shift_vars: list[NurseDecisionVars],
) -> cp_model.LinearExprT:
"""
Apply the constraints and return an optional sub-objective expression.
Subclasses must implement this method to define their specific constraints and objectives.
"""
return 0
For testing, we will use a few auxiliary helper classes that significantly reduce boilerplate code when validating CP-SAT models. These helpers provide an intuitive way to assert whether a model is feasible or infeasible after constraints have been added.
You can install these helpers via pip install cpsat-utils
from cpsat_utils.testing import (
AssertModelFeasible,
AssertModelInfeasible,
assert_objective,
)
with AssertModelFeasible() as model:
# build a model that is supposed to be feasible
# if the model is infeasible, the context manager will raise an error
with AssertModelInfeasible() as model:
# build a model that is supposed to be infeasible
# if the model is feasible, the context manager will raise an error
# assert that the model is feasible and has the expected objective value
assert_objective(model=model, expected=-1.0)
These helpers are particularly useful for test-driven development (TDD) because they keep the tests concise and focused on what should happen, rather than on the mechanics of solving and checking the model. By wrapping the solver logic inside a context manager, you avoid repetitive setup code and make tests easier to read and maintain.
We will write tests using pytest, a
widely used testing framework for Python. With pytest, you simply write
functions that start with test_, and the framework will automatically discover
and execute them. To run all tests, just type pytest in your terminal, and it
will find all test files (named either test_*.py or *_test.py) and run the
contained tests.
Here is a minimal example:
# ./tests/test_example.py
def test_example():
"""
This is a simple example test that always fails.
Use it to verify that your testing framework is set up correctly.
"""
assert False # Make sure you get an error here to confirm the test framework is working.
In order to get some simple test data, we will also write some simple data generation functions.
- create_shifts: Generates a list of shifts with consecutive start times.
- create_nurse: Creates a nurse with a specified name and blocked shifts.
The code is quite simple and you can find it below:
Click to expand the code for data generation
# ./tests/generate.py
"""
A simple utility to create shifts and nurses for testing purposes.
"""
from datetime import datetime, timedelta
from nurserostering.data_schema import Shift, Nurse
def create_shifts(k: int, week: int = 0, shift_length: int = 8) -> list[Shift]:
"""
Create a list of shifts for testing.
Each shift is named "Shift {i}" and has a start time and end time.
"""
shifts = []
for i in range(k):
start_time = (
datetime(2025, 1, 1, 0, 0)
+ timedelta(hours=i * shift_length)
+ timedelta(days=week * 7)
)
end_time = (
datetime(2025, 1, 1, 0, 0)
+ timedelta(hours=(i + 1) * shift_length)
+ timedelta(days=week * 7)
)
shifts.append(
Shift(
name=f"Shift {i + 1}",
start_time=start_time,
end_time=end_time,
demand=2,
)
)
return shifts
def create_nurse(
nurse_name: str = "Test Nurse",
preferred_shifts: set[int] | None = None,
blocked_shifts: set[int] | None = None,
staff: bool = True,
min_time_between_shifts: timedelta = timedelta(hours=8),
) -> Nurse:
"""
Create a nurse with customizable attributes.
"""
if preferred_shifts is None:
preferred_shifts = set()
if blocked_shifts is None:
blocked_shifts = set()
return Nurse(
name=nurse_name,
preferred_shifts=preferred_shifts,
blocked_shifts=blocked_shifts,
staff=staff,
min_time_between_shifts=min_time_between_shifts,
)
No Blocked Shifts
When we begin implementing constraints, it is wise to start with the simplest rule possible. For our nurse rostering problem, one such rule is that a nurse cannot be assigned to a shift if they are explicitly blocked from working that shift. This models situations such as vacations, sick leave, or other forms of unavailability. If this constraint is violated, the schedule is invalid, no matter how good it is otherwise.
We will now apply a test-driven approach to implement this constraint.
Step 1: Writing the First Test (Trivial Feasibility)
Our first test checks the trivial case: a nurse with no blocked shifts should not cause any infeasibility. We do not even need to fix any assignments in this case. The purpose is to verify that the model remains valid when there are no constraints to enforce.
def test_no_blocked_shifts_trivial():
"""
A nurse with no blocked shifts should always lead to a feasible model.
"""
shifts = create_shifts(2) # two consecutive shifts
nurse = create_nurse("Nurse A", blocked_shifts=set())
instance = NurseRosteringInstance(nurses=[nurse], shifts=shifts)
with AssertModelFeasible() as model:
nurse_vars = NurseDecisionVars(nurse, shifts, model)
NoBlockedShiftsModule().build(instance, model, [nurse_vars])
This test will of course fail because we have not yet implemented the
NoBlockedShiftsModule. Let us do that next.
class NoBlockedShiftsModule(ShiftAssignmentModule):
"""
Prohibit assignment to blocked shifts.
"""
def build(
self,
instance: NurseRosteringInstance,
model: cp_model.CpModel,
nurse_shift_vars: list[NurseDecisionVars],
) -> cp_model.LinearExprT:
# TODO
return 0
Now it should pass, as we actually do not enforce any constraints yet. Let us create a second test that will check that we cannot assign a nurse to a shift they are blocked from.
Step 2: Testing Infeasibility for Blocked Shifts
If a nurse is blocked from working a shift but we force them to be assigned to it, the model should become infeasible. This confirms that our constraint actually prevents invalid assignments.
def test_no_blocked_shifts_infeasible():
"""
The model should be infeasible if we assign a nurse to a blocked shift.
"""
shifts = create_shifts(2)
nurse = create_nurse("Nurse A", blocked_shifts={shifts[0].uid})
instance = NurseRosteringInstance(nurses=[nurse], shifts=shifts)
with AssertModelInfeasible() as model:
nurse_vars = NurseDecisionVars(nurse, shifts, model)
NoBlockedShiftsModule().build(instance, model, [nurse_vars])
nurse_vars.fix(shifts[0].uid, True) # Force assignment to a blocked shift
This test should now fail, as we have not yet implemented the logic to enforce
the blocked shifts constraint. Let us implement the logic in the
NoBlockedShiftsModule.
class NoBlockedShiftsModule(ShiftAssignmentModule):
"""
Prohibit assignment to blocked shifts.
"""
def enforce_for_nurse(self, model: cp_model.CpModel, nurse_x: NurseDecisionVars):
for shift_uid in nurse_x.nurse.blocked_shifts:
# Prohibit assignment to blocked shifts
model.add(nurse_x.is_assigned_to(shift_uid=shift_uid) == 0)
def build(
self,
instance: NurseRosteringInstance,
model: cp_model.CpModel,
nurse_shift_vars: list[NurseDecisionVars],
) -> cp_model.LinearExprT:
for nurse_x in nurse_shift_vars:
self.enforce_for_nurse(model, nurse_x)
return 0 # no objective contribution
Step 3: Testing Feasibility on Non-Blocked Shifts
Finally, we check that a nurse can still work on other, non-blocked shifts. Here we assign the nurse to a shift that is allowed, and we expect the model to remain feasible.
def test_no_blocked_shifts_feasible():
"""
A nurse assigned to a non-blocked shift should remain feasible.
"""
shifts = create_shifts(2)
nurse = create_nurse("Nurse A", blocked_shifts={shifts[0].uid})
instance = NurseRosteringInstance(nurses=[nurse], shifts=shifts)
with AssertModelFeasible() as model:
nurse_vars = NurseDecisionVars(nurse, shifts, model)
NoBlockedShiftsModule().build(instance, model, [nurse_vars])
nurse_vars.fix(shifts[1].uid, True) # Assign allowed shift
Our NoBlockedShiftsModule should cover that case as well. In the following
modules, we will not perform the TDD cycle in detail, but we will still describe
the key tests and the implementation of each module. This will keep the focus on
the constraints and objectives rather than the testing mechanics.
 How do you find good test cases? A good rule of thumb is to start with simple cases that cover the basic functionality. Then add edge cases from both sides: create one case that is right on the edge of feasibility, and another that is just outside it. Any scenario that could be off by one is an excellent candidate for an edge case. |
Minimum Off Time
The minimum off time constraint enforces that a nurse cannot work two shifts that are too close together. Formally, for each nurse and for every pair of shifts, if the time between the end of one shift and the start of the next is less than the required rest period, both cannot be assigned to the nurse.
Key Tests
To verify this constraint, we first test with simple assignment patterns:
[None, True, True, None]: infeasible (two consecutive shifts without rest).[True, False, True]: feasible if the gap is long enough.[True, True]: infeasible if two consecutive shifts overlap or violate the minimum rest.
Using a helper function, we can easily run these tests with different parameters:
def run_min_rest_test(
assignments: list[bool|None],
expected_feasible: bool,
shift_length: int = 8,
min_time_in_between: timedelta = timedelta(hours=16),
):
shifts = create_shifts(len(assignments), shift_length=shift_length)
nurse = create_nurse("Nurse A", min_time_between_shifts=min_time_in_between)
instance = NurseRosteringInstance(nurses=[nurse], shifts=shifts)
context = AssertModelFeasible() if expected_feasible else AssertModelInfeasible()
with context as model:
nurse_vars = NurseDecisionVars(nurse, shifts, model)
MinTimeBetweenShifts().build(instance, model, [nurse_vars])
for s, assign in zip(shifts, assignments):
if assign is None:
continue # skip free assignments
nurse_vars.fix(s.uid, assign)
The individual tests can then be defined as follows:
def test_min_time_between_shifts_infeasible_pattern():
run_min_rest_test(
assignments=[None, True, True, None],
expected_feasible=False,
shift_length=8,
min_time_in_between=timedelta(hours=8),
)
def test_min_time_between_shifts_feasible_pattern():
run_min_rest_test(
assignments=[True, False, True],
expected_feasible=True,
shift_length=8,
min_time_in_between=timedelta(hours=8),
)
Additional test cases (e.g., single-shift, all-false, and variable-length gaps) are available in the full test file but omitted here for clarity.
 For testing feasibility, you should fix as many assignments as possible, as each fixed assignment makes it harder for the solver to maneuver around the constraints. For testing infeasibility, you should fix as few assignments as necessary, allowing the solver enough freedom to explore potential ways of circumventing the constraints. |
Implementation
For the implementation, we find for each shift of a nurse all subsequent shifts that would violate the minimum rest time if both were assigned. If the first shift is assigned, then none of these subsequent shifts can be assigned. Here we can optimize the model building by leveraging the fact that the shifts are sorted by start time.
A simpler, but less efficient, implementation would check all pairs of shifts for each nurse, and enforce that only one of them can be assigned.
class MinTimeBetweenShifts(ShiftAssignmentModule):
def enforce_for_nurse(self, model: cp_model.CpModel, nurse_x: NurseDecisionVars):
min_time_between_shifts = nurse_x.nurse.min_time_between_shifts
for i in range(len(nurse_x.shifts) - 1):
shift_i = nurse_x.shifts[i]
colliding: list[Shift] = [] # shifts that are too close to shift_i
for j in range(i + 1, len(nurse_x.shifts)):
shift_j = nurse_x.shifts[j]
if shift_i.end_time + min_time_between_shifts <= shift_j.start_time:
# Since shifts are sorted by start time, if the current shift_j starts
# after the required rest period, all subsequent shifts will also be valid.
# Therefore, we can safely break here to avoid unnecessary checks.
break
colliding.append(shift_j)
if colliding:
# if there are shifts that are too close to shift_i,
# prevent their assignment if shift_i is assigned
shift_i_selected = nurse_x.is_assigned_to(shift_i.uid)
no_colliding_selected = (
sum(nurse_x.is_assigned_to(s.uid) for s in colliding) == 0
)
model.add(no_colliding_selected).only_enforce_if(shift_i_selected)
def build(self, instance, model, nurse_shift_vars):
"""
Enforce minimum rest time between any two shifts for a nurse.
"""
for nv in nurse_shift_vars:
self.enforce_for_nurse(model, nv)
return 0 # no objective contribution
Demand Satisfaction
In the real world, every shift requires a minimum number of nurses to ensure safe and efficient operations. This requirement is captured as the demand of the shift. The demand satisfaction constraint enforces that each shift is assigned at least as many nurses as its demand specifies.
To verify this behavior, we use simple tests. In the first test, we create one shift with a demand of 2 and two available nurses, which is feasible. In the second test, we block the assignment of one of the nurses, which violates the demand requirement and should make the model infeasible.
from nurserostering.modules import DemandSatisfactionModule
from nurserostering.nurse_vars import NurseDecisionVars
from cpsat_utils.testing import AssertModelFeasible, AssertModelInfeasible
from generate import create_shifts, create_nurse
from nurserostering.data_schema import NurseRosteringInstance
def test_demand_satisfaction_met():
shifts = create_shifts(1)
shifts[0].demand = 2
nurse1 = create_nurse("N1")
nurse2 = create_nurse("N2")
instance = NurseRosteringInstance(nurses=[nurse1, nurse2], shifts=shifts)
with AssertModelFeasible() as model:
nurse_vars1 = NurseDecisionVars(nurse1, shifts, model)
nurse_vars2 = NurseDecisionVars(nurse2, shifts, model)
DemandSatisfactionModule().build(instance, model, [nurse_vars1, nurse_vars2])
def test_demand_satisfaction_understaffed():
shifts = create_shifts(1)
shifts[0].demand = 2
nurse1 = create_nurse("N1")
nurse2 = create_nurse("N2")
instance = NurseRosteringInstance(nurses=[nurse1, nurse2], shifts=shifts)
with AssertModelInfeasible() as model:
nurse_vars1 = NurseDecisionVars(nurse1, shifts, model)
nurse_vars2 = NurseDecisionVars(nurse2, shifts, model)
DemandSatisfactionModule().build(instance, model, [nurse_vars1, nurse_vars2])
nurse_vars2.fix(shifts[0].uid, False)
The corresponding implementation of the constraint is equally straightforward: we simply add a constraint that the total number of assigned nurses for a shift must be at least the shift’s demand.
class DemandSatisfactionModule(ShiftAssignmentModule):
"""
Ensure each shift meets its demand.
"""
def build(
self,
instance: NurseRosteringInstance,
model: cp_model.CpModel,
nurse_shift_vars: list[NurseDecisionVars],
) -> cp_model.LinearExprT:
for shift in instance.shifts:
assigned_nurses = [
nurse.is_assigned_to(shift_uid=shift.uid)
for nurse in nurse_shift_vars
if shift.uid in nurse._x
]
model.add(sum(assigned_nurses) >= shift.demand)
return 0
Prefer Staff
While the previous modules defined hard constraints that must be satisfied, this module introduces a soft constraint. We prefer to assign internal staff nurses over contractors, as contractors may be more expensive or less desirable for other reasons. Instead of enforcing this rule strictly, we penalize the use of contractors in the objective function. This way, the solver will try to minimize the number of contractor assignments while still satisfying all hard constraints.
Example Test:
from nurserostering.modules import PreferStaffModule, DemandSatisfactionModule
from cpsat_utils.testing import assert_objective
from generate import create_shifts, create_nurse
from nurserostering.nurse_vars import NurseDecisionVars
from nurserostering.data_schema import NurseRosteringInstance
from ortools.sat.python import cp_model
def test_prefer_staff_module():
"""
Prefer assigning the staff nurse (objective = 0).
"""
shifts = create_shifts(1)
shifts[0].demand = 1
staff = create_nurse("Staff", staff=True)
contractor = create_nurse("Contractor", staff=False)
instance = NurseRosteringInstance(nurses=[staff, contractor], shifts=shifts)
model = cp_model.CpModel()
vars_staff = NurseDecisionVars(staff, shifts, model)
vars_contractor = NurseDecisionVars(contractor, shifts, model)
solver = cp_model.CpSolver()
staff_mod = PreferStaffModule()
DemandSatisfactionModule().build(instance, model, [vars_staff, vars_contractor])
model.minimize(staff_mod.build(instance, model, [vars_staff, vars_contractor]))
assert_objective(model=model, solver=solver, expected=0.0)
assert solver.value(vars_staff.is_assigned_to(shifts[0].uid)) == 1
assert solver.value(vars_contractor.is_assigned_to(shifts[0].uid)) == 0
Implementation:
class PreferStaffModule(ShiftAssignmentModule):
def build(
self,
instance: NurseRosteringInstance,
model: cp_model.CpModel,
nurse_shift_vars: list[NurseDecisionVars],
) -> cp_model.LinearExprT:
"""
Penalize use of non-staff (contract) nurses in the objective.
"""
expr = 0
for nv in nurse_shift_vars:
if not nv.nurse.staff:
for uid in nv._x:
expr += instance.staff_weight * nv.is_assigned_to(uid)
return expr
Preferences Objective
While many of the previous modules focused on enforcing constraints,
MaximizePreferences is different: it defines what we actually want to
optimize. Nurses often have preferences for specific shifts—perhaps due to
personal schedules, skill matching, or desired working hours. A good schedule
should take these preferences into account as much as possible.
The MaximizePreferences module encodes this by assigning a negative
contribution (a reward) to the objective function whenever a nurse is assigned
to one of their preferred shifts. As our interface will minimize by default, we
negate the weight so that preferred assignments reduce the total objective
value. Note that we could have easily specified that the expression returned by
build should be maximized.
This module is therefore not a soft constraint but a true objective: among all feasible schedules, it guides the solver to find one that maximizes nurse satisfaction.
Example Test:
from nurserostering.modules import MaximizePreferences, DemandSatisfactionModule
from cpsat_utils.testing import assert_objective
from generate import create_shifts, create_nurse
from nurserostering.nurse_vars import NurseDecisionVars
from nurserostering.data_schema import NurseRosteringInstance
from ortools.sat.python import cp_model
def test_maximize_preferences_module():
"""
Prefer assigning the nurse to their preferred shift (objective = -1).
"""
shifts = create_shifts(1)
shifts[0].demand = 1
nurse = create_nurse("Preferred Nurse", preferred_shifts={shifts[0].uid})
instance = NurseRosteringInstance(nurses=[nurse], shifts=shifts)
model = cp_model.CpModel()
nurse_vars = NurseDecisionVars(nurse, shifts, model)
solver = cp_model.CpSolver()
pref_mod = MaximizePreferences()
DemandSatisfactionModule().build(instance, model, [nurse_vars])
model.minimize(pref_mod.build(instance, model, [nurse_vars]))
assert_objective(model=model, solver=solver, expected=-1.0)
assert (
solver.value(nurse_vars.is_assigned_to(shifts[0].uid)) == 1
), "Nurse should be assigned to their preferred shift"
Implementation:
class MaximizePreferences(ShiftAssignmentModule):
def build(
self,
instance: NurseRosteringInstance,
model: cp_model.CpModel,
nurse_shift_vars: list[NurseDecisionVars],
) -> cp_model.LinearExprT:
"""
Reward assignments that match nurse preferences by reducing the objective value.
"""
expr = 0
for nv in nurse_shift_vars:
for uid in nv.nurse.preferred_shifts:
expr += -nv.nurse.preferred_shift_weight * nv.is_assigned_to(uid)
return expr
Full Solver
At this point, we have implemented all the necessary modules: the constraints,
soft constraints, and objectives. The next step is to combine these components
into a complete optimization model. The NurseRosteringModel class is
responsible for orchestrating all modules, building the CP-SAT model, and
extracting the solution.
from ortools.sat.python import cp_model
from .nurse_vars import NurseDecisionVars
from .data_schema import NurseRosteringInstance, NurseRosteringSolution
from .modules import (
ShiftAssignmentModule,
NoBlockedShiftsModule,
DemandSatisfactionModule,
MinTimeBetweenShifts,
MaximizePreferences,
PreferStaffModule,
)
class NurseRosteringModel:
"""
A compact and extensible solver for the nurse rostering problem using CP-SAT.
"""
def __init__(
self, instance: NurseRosteringInstance, model: cp_model.CpModel | None = None
):
self.instance = instance
self.model = model or cp_model.CpModel()
self.nurse_vars = [
NurseDecisionVars(nurse, instance.shifts, self.model)
for nurse in instance.nurses
]
self.modules: list[ShiftAssignmentModule] = [
NoBlockedShiftsModule(),
DemandSatisfactionModule(),
MinTimeBetweenShifts(),
MaximizePreferences(),
PreferStaffModule(),
]
objective = sum(
module.build(instance, self.model, self.nurse_vars) # type: ignore
for module in self.modules
)
self.model.minimize(objective)
def solve(
self,
log_search_progress: bool = True,
max_time_in_seconds: float = 60.0,
**solver_params,
) -> NurseRosteringSolution:
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = log_search_progress
solver.parameters.max_time_in_seconds = max_time_in_seconds
for key, value in solver_params.items():
setattr(solver.parameters, key, value)
status = solver.solve(self.model)
if status == cp_model.INFEASIBLE:
raise ValueError("The model is infeasible.")
elif status not in (cp_model.OPTIMAL, cp_model.FEASIBLE):
raise ValueError("Solver failed to find a feasible solution.")
nurses_at_shifts = {}
for nurse_model in self.nurse_vars:
for shift_uid in nurse_model.extract(solver):
nurses_at_shifts.setdefault(shift_uid, []).append(nurse_model.nurse.uid)
return NurseRosteringSolution(
nurses_at_shifts=nurses_at_shifts,
objective_value=round(solver.objective_value),
)
To demonstrate the full workflow, we can test the solver with a small but non-trivial instance. The following test sets up 7 days with 3 shifts per day (morning, day, and night), resulting in 21 shifts. The nurses have a mix of preferences, blocked shifts, and max shift limits, creating an interesting scheduling challenge.
def test_fixed_instance():
base_date = datetime(2025, 1, 1)
shift_length = 8
shifts = []
# 7 days, 3 shifts/day = 21 shifts
for day in range(7):
for idx, hour in enumerate([0, 8, 16]): # Morning, Day, Night
start = base_date + timedelta(days=day, hours=hour)
end = start + timedelta(hours=shift_length)
shifts.append(
Shift(
name=f"Day {day+1} Shift {idx+1}",
start_time=start,
end_time=end,
demand=2 if hour == 8 else 1, # Higher demand for day shifts
)
)
# Total demand: 7*2 (day) + 7*1 (morning) + 7*1 (night) = 28 + 7 + 7 = 42 shifts needed
nurses = [
Nurse(
name="Alice (prefers mornings, no Sundays)",
preferred_shifts={s.uid for s in shifts if s.start_time.hour == 0},
blocked_shifts={s.uid for s in shifts if s.start_time.weekday() == 6},
staff=True,
min_time_between_shifts=timedelta(hours=10),
preferred_shift_weight=3,
),
Nurse(
name="Bob (prefers nights)",
preferred_shifts={s.uid for s in shifts if s.start_time.hour == 16},
blocked_shifts=set(),
staff=True,
min_time_between_shifts=timedelta(hours=10),
preferred_shift_weight=3,
),
Nurse(
name="Clara (prefers weekends, blocks weekdays)",
preferred_shifts={
s.uid for s in shifts if s.start_time.weekday() in {5, 6}
},
blocked_shifts={s.uid for s in shifts if s.start_time.weekday() < 5},
staff=True,
min_time_between_shifts=timedelta(hours=10),
preferred_shift_weight=2,
),
Nurse(
name="Dan (no preferences)",
preferred_shifts=set(),
blocked_shifts=set(),
staff=True,
min_time_between_shifts=timedelta(hours=8),
preferred_shift_weight=1,
),
Nurse(
name="Eve (contractor, prefers day shifts)",
preferred_shifts={s.uid for s in shifts if s.start_time.hour == 8},
blocked_shifts=set(),
staff=False,
min_time_between_shifts=timedelta(hours=10),
preferred_shift_weight=2,
),
Nurse(
name="Frank (prefers day shifts)",
preferred_shifts={s.uid for s in shifts if s.start_time.hour == 8},
blocked_shifts=set(),
staff=True,
min_time_between_shifts=timedelta(hours=10),
preferred_shift_weight=2,
),
Nurse(
name="Grace (prefers mornings)",
preferred_shifts={s.uid for s in shifts if s.start_time.hour == 0},
blocked_shifts=set(),
staff=True,
min_time_between_shifts=timedelta(hours=10),
preferred_shift_weight=3,
),
Nurse(
name="Heidi (contractor, no preferences)",
preferred_shifts=set(),
blocked_shifts=set(),
staff=False,
min_time_between_shifts=timedelta(hours=8),
preferred_shift_weight=1,
),
]
instance = NurseRosteringInstance(
nurses=nurses, shifts=sorted(shifts, key=lambda s: s.start_time), staff_weight=2
)
model = NurseRosteringModel(instance)
solution = model.solve()
assert solution is not None, "The solution should not be None"
assert_solution_is_feasible(instance, solution)
Nurses
| Name & Description | Staff/Contractor | Min Rest | Preferences | Blocked Shifts |
|---|---|---|---|---|
| Alice (prefers mornings, no Sundays) | Staff | ≥ 10h | 7 shifts (weight 3) | 3 shifts |
| Bob (prefers nights) | Staff | ≥ 10h | 7 shifts (weight 3) | — |
| Clara (prefers weekends, blocks weekdays) | Staff | ≥ 10h | 6 shifts (weight 2) | 15 shifts |
| Dan (no preferences) | Staff | ≥ 8h | — | — |
| Eve (contractor, prefers day shifts) | Contractor | ≥ 10h | 7 shifts (weight 2) | — |
| Frank (prefers day shifts) | Staff | ≥ 10h | 7 shifts (weight 2) | — |
| Grace (prefers mornings) | Staff | ≥ 10h | 7 shifts (weight 3) | — |
| Heidi (contractor, no preferences) | Contractor | ≥ 8h | — | — |
Shift Coverage
| Day | Morning (S1) | Day (S2) | Night (S3) |
|---|---|---|---|
| D1 | Alice, Grace | Dan, Frank | Bob |
| D2 | Alice, Grace | Dan, Frank | Bob |
| D3 | Alice, Grace | Eve, Frank | Bob |
| D4 | Alice, Clara, Grace | Dan, Frank | Bob |
| D5 | Clara, Grace | Eve, Frank | Bob |
| D6 | Alice, Grace | Eve, Frank | Bob |
| D7 | Alice, Grace | Dan, Frank | Bob |
Automatic Test Extraction from Production
Because we use pydantic for input and output, serializing test cases from production is straightforward. You can save instances and solutions to JSON and re-load them later for regression tests.
# export instance and solution to JSON
with open("instance.json", "w") as f:
f.write(instance.model_dump_json())
with open("solution.json", "w") as f:
f.write(solution.model_dump_json())
You can then load these files in your tests:
from nurserostering.data_schema import NurseRosteringInstance, NurseRosteringSolution
def test_load_instance_and_solution():
with open("instance.json", "r") as f:
instance = NurseRosteringInstance.model_validate_json(f.read())
with open("solution.json", "r") as f:
solution = NurseRosteringSolution.model_validate_json(f.read())
assert instance is not None, "Instance should not be None"
assert solution is not None, "Solution should not be None"
# should still be feasible
assert_solution_is_feasible(instance, solution)
# reoptimize the solution
model = NurseRosteringModel(instance)
new_solution = model.solve(max_time_in_seconds=10.0)
assert new_solution is not None, "New solution should not be None"
assert_solution_is_feasible(instance, new_solution)
assert new_solution.objective_value == solution.objective_value, "Objective value should match"
Actually, you can also just dump them into a folder and then make the test iterate over all the files in that folder. Instead of just writing the objective value into the solution, you could also add the time it took to solve the instance, which can be useful for performance testing. With a bunch of such files collected, you could then start to refactor and optimize your code, with a minimum of regression risk in correctness or performance. However, keep in mind that the performance of CP-SAT (and other such solvers) can vary between runs, so do not be too strict with the performance tests.
Instead of relying solely on historical data for testing, you can shadow your production model with a development or experimental model. This approach allows you not only to verify correctness but also to directly compare the performance of both models, providing strong confidence that your modifications enhance the model without disrupting production. If you already have a monitoring tool in place, integrating shadow solutions is likely straightforward. This technique is so popular that nextmv offers built-in support for it.
Property-based Testing
As a final point, I briefly discuss property-based testing. Richard Oberdieck, a senior optimizer with expertise in testing, favors this approach and considers unit-based testing less suitable for his purposes. He argues that optimization models are difficult to decompose and that testing individual equations has limited value.
The problem in this chapter has been deliberately simplified. In typical projects, my unit tests target constraints or modules that consist of sets of lower-level constraints and equations. Many of the tests presented here are indeed excessive for the simplified setting.
These observations underscore that no single workflow fits all applications; you should not force my personal style onto your needs. I also vary my approach substantially depending on the problem and context. Property-based testing may be a strong fit for your needs; therefore, I now briefly outline its core ideas.
Property-based testing is a methodology in which you specify general properties that your code must satisfy and then rely on a tool to automatically generate a wide range of test cases to verify these properties. This approach is particularly valuable for optimization problems, where the solution space is large and complex. Conceptually, it resembles automated sampling of possible inputs and checking whether the corresponding outputs fulfill the required criteria.
Unlike naive random testing, libraries such as Hypothesis use strategies to systematically generate inputs and, if a failure occurs, they attempt to shrink the failing case to a minimal counterexample. Hypothesis also stores examples so that failures can be reproduced deterministically.
If, like me, you were initially taught that tests should be deterministic, this may appear unsettling. However, in practice you only need to encounter a bug once; afterward, you can add a deterministic regression test to ensure it does not reoccur. When you are uncertain which edge cases to test, property-based testing provides an effective way to uncover them.
One widely used Python library for property-based testing is Hypothesis. It enables you to define strategies for generating test data and then automatically executes your tests with a diverse set of inputs.
|
A clear and engaging introduction to property-based testing with Hypothesis is provided in this 21-minute YouTube video by ArjanCode.  |
With property-based testing, the guiding questions typically take the following form:
- For any valid instance of my optimization problem, does the solver return a feasible solution (or report infeasibility correctly)?
- For any valid instance of the nurse rostering problem, is there always sufficient staffing to cover every shift?
The phrase “for any valid instance” is central: you must specify to Hypothesis how to generate inputs that satisfy schema invariants. Hypothesis then attempts to falsify your assumption by searching for counterexamples, often targeting edge cases. This approach complements unit tests: you still want a small set of clear, deterministic unit tests for well-understood components, while using property-based tests to explore a much wider space of inputs without bloating the test suite.
Let us begin with a simple example of a property-based test to illustrate the
basic concept. In this case, we test the built-in sorted function and verify
three properties:
from collections import Counter
from hypothesis import given, strategies as st
@given(st.lists(st.integers()))
def test_sort_properties(xs):
sorted_xs = sorted(xs)
# Property 1: Sorting does not change the length
assert len(sorted_xs) == len(xs)
# Property 2: Sorted list is monotonically non-decreasing
for a, b in zip(sorted_xs, sorted_xs[1:]):
assert a <= b
# Property 3: Sorting does not lose or duplicate elements
assert Counter(sorted_xs) == Counter(xs)
In this example, we verify that for any list of integers, applying sorted
preserves the list length, produces a sequence in non-decreasing order, and
returns a permutation of the input. Hypothesis automatically generates a wide
variety of integer lists, runs the test against them, and shrinks any failures
to the smallest counterexample.
Here would be the inputs that hypothesis tested automatically:
[][0][26242, -1963][-121][8436][15719][-19093982987237563430026067407172463954][-3922][-3922, 1364][-923437505601415702][-923437505601415702, 1030000614][-923437505601415702, -923437505601415702][-28265][-30093, -2983, -30440][-30093, -30440, -30440][-30093][-40, 111940892136851798167905802830994768244, -28043, 7, 20215, 1370480367, 7446, -39][-40, 111940892136851798167905802830994768244, -28043, 7, 20215, 1370480367, 20215, -39][-40, 111940892136851798167905802830994768244, 111940892136851798167905802830994768244, 7, 20215, 1370480367, 20215, -39][-40, 111940892136851798167905802830994768244, 111940892136851798167905802830994768244, 7, -39, 1370480367, 20215, -39][-40, 111940892136851798167905802830994768244, 111940892136851798167905802830994768244, 7, 111940892136851798167905802830994768244, 1370480367, 20215, -39][1370480367, 111940892136851798167905802830994768244, 111940892136851798167905802830994768244, 7, 111940892136851798167905802830994768244, 1370480367, 20215, -39][1370480367, 1370480367, 111940892136851798167905802830994768244, 7, 111940892136851798167905802830994768244, 1370480367, 20215, -39][8328, 6129][8328][-114, 12990, -114, 27, -16229, -19256, 928][-114, 12990, -114, 27, -16229, -16229, 928][-114, 12990, -114, 27, -16229, -114, 928][-114, 12990, -114, -114, -16229, -114, 928][-114, 12990, -114, -114, -16229, 928, 928][-114, 12990, -114, -114, -16229, 928, -114][-114, 12990, -114, -114, 928, 928, 928][-7, -79, -1133414645][-79, -79, -1133414645][-79, -79, -79][-1482, -30293, -23505, -7340][-22323, 93][-22323, -22323][2353, 13157][2353, 2353][2353][7714][13297, -12682, -26, 2588, -5696, 18, 10030, 22][13297, -12682, -26, 2588, -5696, 18, 22, 22][13297, -12682, -26, 2588, -5696, 18][13297, 2588, -26, 2588, -5696, 18][13297, 2588, -26][23480, -82, 46, 26111, 32207, -3830610785522322019, 63408623014671325114394083743435908480, 61, -20775, -1100012486, 0, -5724957629946085877, -1248, 64, 21, 13771, 721, 4, 81, -11615, -75, -31640, -15547, -5831, 2113][23480, -82, 46, 26111, 32207, -3830610785522322019, 63408623014671325114394083743435908480, 61, -20775, -1100012486, 0, -5724957629946085877, -1248, 64, 21, 2113, 721, 4, 81, -11615, -75, -31640, -15547, -5831, 2113][23480, -82, 46, 26111, 32207, -3830610785522322019, 63408623014671325114394083743435908480, 61, -20775, -1100012486, 0, -5724957629946085877, -1248, 64, 21][23480, -82, 46, 26111, 32207, -3830610785522322019, 63408623014671325114394083743435908480, 61, -20775, -1100012486, 0, -5724957629946085877, -1248, 21, 21][23480, -82, -1248, 26111, 32207, -3830610785522322019, 63408623014671325114394083743435908480, 61, -20775, -1100012486, 0, -5724957629946085877, -1248, 21, 21][23480, -82, -1248, 26111, 32207, -3830610785522322019, 63408623014671325114394083743435908480, 61, -20775, -1100012486, 0, -5724957629946085877, -1248, 61, 21][23480, -82, -1248, 26111, 63408623014671325114394083743435908480, -3830610785522322019, 63408623014671325114394083743435908480, 61, -20775, -1100012486, 0, -5724957629946085877, -1248, 61, 21][-78711666441691544779522005139678058413, 9413, -28, -25429, 1138913225, 119, 15206, -14631, 13620, 22066, 73, -930][-78711666441691544779522005139678058413, 22066, -28, -25429, 1138913225, 119, 15206, -14631, 13620, 22066, 73, -930][-78711666441691544779522005139678058413, 22066, -28, 119, 1138913225, 119, 15206, -14631, 13620, 22066, 73, -930][-78711666441691544779522005139678058413, 15206, -28, 119, 1138913225, 119, 15206, -14631, 13620, 22066, 73, -930][119, 15206, -28, 119, 1138913225, 119, 15206, -14631, 13620, 22066, 73, -930][119, 15206, -28, 73, 1138913225, 119, 15206, -14631, 13620, 22066, 73, -930][119, 15206, -28, 73, 1138913225, 73, 15206, -14631, 13620, 22066, 73, -930][-10367, -28534][-10367, -10367][-15, -97, 20993, 86, -3483807830384175452, 17981, 5590988155335024430, 21910677380750136143640822796681648827, -11734, 10, -23457][-15, -97, 20993, 86, -3483807830384175452, 17981, 5590988155335024430, -11734, -11734, 10, -23457][-15, -97, 20993, 86, -3483807830384175452, 17981, 5590988155335024430, -23457, -11734, 10, -23457][-15, 10, 20993, 86, -3483807830384175452, 17981, 5590988155335024430, -23457, -11734, 10, -23457][-15, 10, 20993, 86, -3483807830384175452, 17981, 5590988155335024430, -11734, -11734, 10, -23457][-15, 10, 20993, 86, -3483807830384175452, 17981, 5590988155335024430, -11734, 17981, 10, -23457][29141, -30, -5793, 102, -16130, -5, -9949, 676613804, -61, 12368][29141, -30, -5793, 102, 676613804, -5, -9949, 676613804, -61, 12368][-61, -30, -5793, 102, 676613804, -5, -9949, 676613804, -61, 12368][-61, -9949, -5793, 102, 676613804, -5, -9949, 676613804, -61, 12368][-61, -9949, 12368, 102, 676613804, -5, -9949, 676613804, -61, 12368][-61, -9949, 12368, 102, 676613804, -5, -61, 676613804, -61, 12368][105, -124, 29994, 4704, 23985, 5651302969633935431, -21152, 476047859, 23285, 7392, 12][23285, -124, 29994, 4704, 23985, 5651302969633935431, -21152, 476047859, 23285, 7392, 12][23285, -124, 29994, 4704, 5651302969633935431, 5651302969633935431, -21152, 476047859, 23285, 7392, 12][23285, -124, 29994, 23285, 5651302969633935431, 5651302969633935431, -21152, 476047859, 23285, 7392, 12][23285, -124, 29994, 23285, 7392, 5651302969633935431, -21152, 476047859, 23285, 7392, 12][23285, -124, 29994, 7392, 7392, 5651302969633935431, -21152, 476047859, 23285, 7392, 12][2105491908, 8597804526551328604, 7275042865703570734][2105491908, 2105491908, 7275042865703570734][2105491908, 7275042865703570734, 7275042865703570734][7275042865703570734, 2105491908, 7275042865703570734][2105491908, 2105491908, 2105491908][29243, -1704064901, 29484][29243, 29484, 29484][29484, 29484, 29484][-19703, -88, -6578, 121][1070832594, 17504][1070832594, 1070832594][-69][15301, 479652285201667946][479652285201667946, 479652285201667946][479652285201667946][516195269, 10059, -61, -106, 6213, -83, -15699][6213, 10059, -61, -106, 6213, -83, -15699][6213, 10059, -61, -106, 6213, -83, -83][6213, 10059, -61, -106, -83, -83, -83]
We now apply property-based testing to the nurse rostering problem. The central challenge is to define a strategy that generates valid instances of the problem. In particular, the generated instances must satisfy the data schema: unique UIDs; valid time intervals for shifts; and consistent references between nurses, shifts, and assignments. Because constructing instances that are always feasible is difficult, we instead check the following property: within a fixed time limit, the solver either returns a feasible solution that passes an independent validator or reports the instance as infeasible or unknown. This choice may miss false infeasibilities but suffices for this illustrative example.
from datetime import datetime, timedelta
from hypothesis import given, strategies as st
from hypothesis.strategies import composite
from nurserostering.data_schema import NurseRosteringInstance, Shift, Nurse
from nurserostering.solver import NurseRosteringModel
from nurserostering.validation import assert_solution_is_feasible
# --- Helper strategies ---
# A datetime in Jan 2025
_dt_jan_2025 = st.datetimes(
min_value=datetime(2025, 1, 1, 0, 0, 0),
max_value=datetime(2025, 1, 31, 23, 59, 59),
)
@composite
def shift_strategy(draw):
"""
Build a Shift with end_time > start_time.
"""
name = draw(st.text(min_size=1, max_size=10))
start = draw(_dt_jan_2025)
# Duration between 4h and 12h
duration_hours = draw(st.integers(min_value=4, max_value=12))
end = start + timedelta(hours=duration_hours)
# Demand can be zero per schema (NonNegativeInt); keep small
demand = draw(st.integers(min_value=0, max_value=3))
# uid is auto-generated by schema default_factory
return Shift(
name=name,
start_time=start,
end_time=end,
demand=demand,
)
def _subset_of_uids(shift_uids, max_size=5):
"""
Produce a strategy for a set subset of the given shift_uids.
"""
# sampled_from requires a sequence, not a set
return st.sets(
st.sampled_from(list(shift_uids)),
max_size=max_size,
)
@composite
def nurse_strategy(draw, shift_uids):
"""
Build a Nurse whose preferred/blocked sets are subsets of the provided shift_uids.
"""
name = draw(st.text(min_size=1, max_size=10))
staff = draw(st.booleans())
min_tbs = timedelta(hours=8) # fixed, as in your original
pref_weight = draw(st.integers(min_value=0, max_value=5)) # NonNegativeInt
# Independent subsets; may overlap (schema does not forbid)
preferred = draw(_subset_of_uids(shift_uids, max_size=5))
blocked = draw(_subset_of_uids(shift_uids, max_size=5))
# uid is auto-generated by schema default_factory
return Nurse(
name=name,
preferred_shifts=preferred,
blocked_shifts=blocked,
staff=staff,
min_time_between_shifts=min_tbs,
preferred_shift_weight=pref_weight,
)
@composite
def instance_strategy(draw):
"""
Build a NurseRosteringInstance that passes all schema validators:
- Unique nurse/shift UIDs (handled by defaults).
- Shifts sorted by start_time.
- Nurses' preference/blocked sets reference existing shift UIDs.
"""
# Make and sort shifts by start_time
num_shifts = draw(st.integers(min_value=10, max_value=20))
shifts = [draw(shift_strategy()) for _ in range(num_shifts)]
shifts.sort(key=lambda s: s.start_time)
shift_uids = [s.uid for s in shifts]
# Build nurses referencing these shift_uids
num_nurses = draw(st.integers(min_value=5, max_value=10))
nurses = [draw(nurse_strategy(shift_uids)) for _ in range(num_nurses)]
staff_weight = draw(st.integers(min_value=0, max_value=5))
return NurseRosteringInstance(
nurses=nurses,
shifts=shifts,
staff_weight=staff_weight,
)
# --- Property test ---
@given(instance=instance_strategy())
def test_solver_finds_feasible_solution(instance):
model = NurseRosteringModel(instance)
try:
solution = model.solve(max_time_in_seconds=10.0)
assert_solution_is_feasible(instance, solution)
except ValueError:
# If the model is infeasible, we accept that as a valid outcome.
# Ensuring that the input is feasible would be a little more complex.
pass
 See Richard Oberdieck’s example repository, which demonstrates property-based testing for an optimization problem using Hypothesis. Consult the /docs directory for additional textual explanation; note that the documentation is incomplete at present. |
Conclusion
In this chapter, we developed a complete nurse rostering solver using CP-SAT within a test-driven framework. The modular design enabled us to separate constraints from objectives, create targeted tests, and iterate with confidence. While this methodology is not always the fastest path to a working solution, it proves highly effective for problems that evolve over time.
We also highlighted alternative approaches—such as tabular data representations and property-based testing—emphasizing that you should select the methods that best suit your specific context. The key takeaway is that software engineering principles can be successfully applied to optimization modeling, thereby enhancing both reliability and maintainability.
 This chapter primarily emphasized correctness. However, once your solution is working correctly, you may discover that it does not scale sufficiently well. In the chapter Benchmarking your Model, you will learn how to benchmark models to evaluate improvements in performance and scalability. The testing framework developed here helps maintain correctness during performance optimization. Frequently, enhancing efficiency involves slight modifications to the problem formulation—such as approximating non-linear elements with linear ones or relaxing constraints that can usually be repaired in postprocessing with minimal loss of solution quality. Adapting these changes may require adjustments to your tests, but typically you can reuse many of them. |
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Building an Optimization API (DRAFT)
In this chapter, we will create a basic optimization service that performs computations on a cluster rather than on the client side. This service can be extended with a straightforward frontend, allowing non-technical users to access the optimization capabilities. By encapsulating your optimization code within an easy-to-use API, integration into larger systems becomes more streamlined, and the separation of algorithm development from deployment is achieved.
While this chapter does not cover every aspect of building a production-ready API, it will address many important points of it. This foundational knowledge will enable you to collaborate effectively with your integration experts to finalize the implementation details, or even do it yourself.
To illustrate these principles, we will develop a simple optimization model for the Traveling Salesman Problem (TSP). Users will be able to submit an instance of the TSP, and the API will return a solution. The primary challenge, compared to many other APIs, is that the TSP is an NP-hard problem, and the CP-SAT solver may need several minutes to solve even moderately sized instances. Additionally, we cannot run the solver on the web server; instead, we must distribute the computation across a cluster. If many requests are received simultaneously, a request may need to wait before computation can start.
Therefore, this will not be a simple “send request, get response” API. Instead, we will implement a task queue, returning a task ID that users can use to check the status of their computation and retrieve the result once it is ready. To enhance user experience, we will allow users to specify a webhook URL, which we will call once the computation is complete.
You should be able to easily adapt this API to your own optimization problems, allowing you to quickly service your optimization algorithms to your colleagues.
Specifying the Essential Endpoints
Before we start coding, we should specify the endpoints our API will expose, so we know what we need to implement. This is something you can directly share with the coworkers who will implement the frontend or other parts of the system, so they know what to expect and can start working on their parts. It is usually simple to change the details of the payloads later, but changing the flow of the API can be much more complex.
The fundamental operations we will support are:
- POST /jobs: This endpoint will accept a JSON payload containing the TSP instance. The API will create a new task, store the instance, and return a task ID. The payload will also allow users to specify a webhook URL to call once the computation is complete.
- GET /jobs/{task_id}: This endpoint will return the status of the task with the given ID.
- GET /jobs/{task_id}/solution: This endpoint will return the solution of the task with the given ID, once it is available.
- DELETE /jobs/{task_id}: This endpoint will cancel the task with the given ID.
- GET /jobs: This endpoint will return a list of all tasks, including their status and metadata.
By defining these endpoints, we ensure that our API is robust and capable of handling the core functionalities required for managing and solving TSP instances. This structure will facilitate user interactions, from submitting tasks to retrieving solutions and monitoring the status of their requests.
Once we have successfully launched or TSP optimization service, we can
anticipate requests to extend our optimization capabilities to other problems.
Therefore, we should add the prefix /tsp_solver/v1 to all endpoints to
facilitate future expansions of our API with additional solvers, e.g.,
knapsack_solver/v1, or /tsp_solver/v2_experimental.
You may ask why we do not just create a new project for each solver and then just stick them together on a higher level. The reason is that we may want to share the same infrastructure for all solvers, especially the task queue and the worker cluster. This can not only be easier to maintain, but also cheaper as resources can be shared. Therefore, it makes sense to keep them in the same project. However, it will make sense to separate the actual algorithms from the API code, and only import the algorithms into our API project. We will not do this in this chapter, but I personally prefer the algorithms to be as separated as possible as they are often complex enough on their own.
Architecture
Having outlined the requirements, we will now consider the architecture of our system. The system will incorporate the following components:
-
FastAPI for implementing the endpoints: FastAPI is a modern, high-performance web framework for building APIs with Python. We will use FastAPI to define API endpoints and handle HTTP requests due to its simplicity, speed, and automatic interactive API documentation.
-
Redis as a database and communication interface with the workers: Redis is an in-memory data structure store that can function as a database, cache, and message broker. We will utilize Redis for its speed and efficiency in storing and sharing tasks and solutions, which allows quick access and automatic expiration of data when it is no longer needed.
-
Workers managed with RQ (Redis Queue): RQ is a simple Python library for queuing jobs and processing them in the background with workers. This enables our API to handle tasks asynchronously, offloading computationally expensive processes to background workers and thereby improving the API’s responsiveness.
To easily manage these components, we will use Docker and Docker Compose to containerize the API, Redis, and worker instances. This will allow us to quickly set up and run the service either locally or in a cloud environment.
 We will ignore security aspects in this chapter. This service should be only for internal use within the own network and not be exposed to the internet. If you want to expose it, you should add authentication, rate limiting, and other security measures. |
Project Structure
As we only have a single solver in this project, we will neither separate the solver from the API nor encapsulate the API, but use a simple, flat structure. You can find the complete project in ./examples/optimization_api.
├── app
│ ├── __init__.py
│ ├── config.py
│ ├── db.py
│ ├── main.py
│ ├── models.py
│ ├── solver.py
│ └── tasks.py
├── docker-compose.yml
├── Dockerfile
└── requirements.txt
Let us quickly go through the components of the project:
-
Requirements: We define the necessary Python packages in a
requirements.txtfile to ensure that the environment can be easily set up and replicated. This file includes all dependencies needed for the project.requirements.txtare rather outdated, but they are the simplest way to just install the dependencies in our container. -
Docker Environment:
Dockerfile: The Dockerfile specifies the Docker image and environment setup for the API. It ensures that the application runs in a consistent environment across different machines.docker-compose.yml: This file configures the services required for the project, including the API, Redis, and worker instances. Docker Compose simplifies the process of managing multiple containers, ensuring they are correctly built and started in the right order. A simpledocker-compose up -d --buildwill get the whole system up and running.
-
Solver Implementation:
./app/solver.py: This module contains the implementation of the TSP solver using CP-SAT. It also specifies the expected input and output data.
-
Request and Response Models:
./app/models.py: This module specifies further data models for API requests and responses.
-
Database:
./app/db.py: This module implements a proxy class to interact with Redis, abstracting database operations for storing and retrieving job requests, statuses, and solutions.
-
Config:
./app/config.py: This module provides configuration functions to set up the database connection and task queue. By centralizing configuration, we ensure that other parts of the application do not need to manage connection details, making the codebase more modular and easier to maintain.
-
Tasks:
./app/tasks.py: This module defines the tasks to be outsourced to workers, which right now only includes the optimization job. Our web server will only need to get a reference to the task functions in order to queue them, but not actually run anything of this code. For the workers, this file will be the entry point.
-
API:
./app/main.py: This module implements the FastAPI application with routes for submitting jobs, checking job statuses, retrieving solutions, and canceling jobs. This is the entry point for the web server.
Running the Application
To run the application, we use Docker and Docker Compose to build and run the containers. This ensures the API and its dependencies are correctly set up. Once the containers are running, you can interact with the API via HTTP requests.
Docker Environment
We use Docker to ensure a consistent development and production environment.
Docker allows us to package our application with all its dependencies into a
standardized unit for software development. Docker Compose is used to manage
multi-container applications, defining and running multi-container Docker
applications. As the web server and the workers essentially share the same code,
just with different entry points, we can use the same Docker image for both. The
different entry points will be specified in the docker-compose.yml.
Dockerfile
# Use an official Python runtime as a parent image
FROM python:3.12-slim
# Set the working directory in the container
WORKDIR /app
# Copy the requirements file into the container at /app
COPY requirements.txt /
# Install any needed packages specified in requirements.txt
RUN pip install --no-cache-dir -r /requirements.txt
# Copy the current directory contents into the container at /app
COPY ./app /app
docker-compose.yml
To get our composition of containers, with the API, Redis, and the workers up
and running, we use the following docker-compose.yml file:
services:
optimization_api_fastapi: # The web server
build: .
container_name: optimization_api_fastapi
ports: # exposing the API on port 80. Change this if you want to use a different port.
- "80:80"
depends_on: # Ensuring that the web server starts after the database.
- optimization_api_redis
command: python3 -m uvicorn main:app --host 0.0.0.0 --port 80 --reload
optimization_api_redis: # The database. We use the official Redis image.
image: redis:latest
container_name: optimization_api_redis
optimization_api_worker: # The worker
build: .
command: # Running this command will make our container a worker instead of a web server.
rq worker --with-scheduler --url redis://optimization_api_redis:6379/1
depends_on: # Ensuring that the worker starts after the database, as it needs to connect to it.
- optimization_api_redis
deploy:
replicas: 2 # Adding two workers for parallel processing
The docker-compose.yml file sets up three services:
optimization_api_fastapi: This service builds the FastAPI application, exposes it on port 80, and ensures it starts after Redis is available.optimization_api_redis: This service sets up the Redis database from the official Redis image. We just need to remember the name of the container to connect to it.optimization_api_worker: This service builds the worker, which processes tasks from the queue. We can scale the number of workers by increasing the number of replicas. Theoretically, these workers could be run on different machines to scale horizontally.
Solver
In this section, we will explore the implementation of the optimization
algorithm that we will deploy as an API. Specifically, we will focus on a simple
implementation of the Traveling Salesman Problem (TSP) using the add_circuit
constraint from the CP-SAT solver in OR-Tools.
The solver is the core component of our application, responsible for finding the optimal solution to the TSP instance provided by the user. The algorithm is implemented directly in the API project for simplicity. However, for more complex optimization algorithms, it is advisable to separate the algorithm into a distinct module or project. This separation facilitates isolated testing and benchmarking of the algorithm and improves the development process, especially when working in a team where different teams might maintain the API and the optimization algorithm.
# ./app/solver.py
from typing import Callable
from ortools.sat.python import cp_model
from pydantic import BaseModel, Field
# ---------------------------------------------------------------------
# A precise definition of the input and output data for the TSP solver.
# ---------------------------------------------------------------------
class DirectedEdge(BaseModel):
source: int = Field(..., ge=0, description="The source node of the edge.")
target: int = Field(..., ge=0, description="The target node of the edge.")
cost: int = Field(..., ge=0, description="The cost of traversing the edge.")
class TspInstance(BaseModel):
num_nodes: int = Field(
..., gt=0, description="The number of nodes in the TSP instance."
)
edges: list[DirectedEdge] = Field(
..., description="The directed edges of the TSP instance."
)
class OptimizationParameters(BaseModel):
timeout: int = Field(
default=60,
gt=0,
description="The maximum time in seconds to run the optimization.",
)
class TspSolution(BaseModel):
node_order: list[int] | None = Field(
..., description="The order of the nodes in the solution."
)
cost: float = Field(..., description="The cost of the solution.")
lower_bound: float = Field(..., description="The lower bound of the solution.")
is_infeasible: bool = Field(
default=False, description="Whether the instance is infeasible."
)
# ---------------------------------------------------------------------
# The TSP solver implementation using the CP-SAT solver from OR-Tools.
# ---------------------------------------------------------------------
class TspSolver:
def __init__(
self, tsp_instance: TspInstance, optimization_parameters: OptimizationParameters
):
self.tsp_instance = tsp_instance
self.optimization_parameters = optimization_parameters
self.model = cp_model.CpModel()
self.edge_vars = {
(edge.source, edge.target): self.model.new_bool_var(
f"x_{edge.source}_{edge.target}"
)
for edge in tsp_instance.edges
}
self.model.minimize(
sum(
edge.cost * self.edge_vars[(edge.source, edge.target)]
for edge in tsp_instance.edges
)
)
self.model.add_circuit(
[(source, target, var) for (source, target), var in self.edge_vars.items()]
)
def solve(self, log_callback: Callable[[str], None] | None = None):
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = self.optimization_parameters.timeout
if log_callback:
solver.parameters.log_search_progress = True
solver.log_callback = log_callback
status = solver.Solve(self.model)
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
return TspSolution(
node_order=[
source
for (source, target), var in self.edge_vars.items()
if solver.value(var)
],
cost=solver.objective_value,
lower_bound=solver.best_objective_bound,
)
if status == cp_model.INFEASIBLE:
return TspSolution(
node_order=None,
cost=float("inf"),
lower_bound=float("inf"),
is_infeasible=True,
)
return TspSolution(
node_order=None,
cost=float("inf"),
lower_bound=solver.best_objective_bound,
)
 CP-SAT itself uses Protobuf for its input, output, and configuration. Having well-defined data models can help prevent many “garbage in, garbage out” issues and ease integration with other systems. It also facilitates testing and debugging, as you can simply serialize a specific scenario. For configuration, having default values is very helpful, as it allows you to extend the configuration without breaking backward compatibility. This can be a significant advantage, as you usually do not know all requirements upfront. Pydantic performs this job very well and can be used for the web API as well. Protobuf, while not Python-specific and therefore more versatile, is more complex to use and lacks the same flexibility as Pydantic. |
Request and Response Models
In this section, we will define the request and response models for the API. These models will facilitate the communication between the client and the server by ensuring that the data exchanged is structured and validated correctly.
The models are defined in the models.py file and include the necessary data
structures for submitting a TSP job request and tracking the status of the job.
# ./app/models.py
"""
This file contains the implementation of additional data models for the optimization API.
"""
from datetime import datetime
from pydantic import BaseModel, HttpUrl, Field
from uuid import UUID, uuid4
from solver import OptimizationParameters, TspInstance
The TspJobRequest model encapsulates the information required to submit a TSP
job to the API. It includes the TSP instance, optimization parameters, and an
optional webhook URL for notifications upon job completion.
class TspJobRequest(BaseModel):
"""
A request model for a TSP job.
"""
tsp_instance: TspInstance = Field(..., description="The TSP instance to solve.")
optimization_parameters: OptimizationParameters = Field(
default_factory=OptimizationParameters,
description="The optimization parameters.",
)
webhook_url: HttpUrl | None = Field(
default=None, description="The URL to call once the computation is complete."
)
An request could look as follows:
{
"tsp_instance": {
"num_nodes": 4,
"edges": [
{"source": 0, "target": 1, "cost": 1},
{"source": 1, "target": 2, "cost": 2},
{"source": 2, "target": 3, "cost": 3},
{"source": 3, "target": 0, "cost": 4},
],
},
"optimization_parameters": {"timeout": 5},
"webhook_url": null,
},
The TspJobStatus model is used to track the status of a TSP job. It provides
fields to monitor various stages of the job lifecycle, from submission to
completion.
class TspJobStatus(BaseModel):
"""
A response model for the status of a TSP job.
"""
task_id: UUID = Field(default_factory=uuid4, description="The ID of the task.")
status: str = Field(default="Submitted", description="The status of the task.")
submitted_at: datetime = Field(
default_factory=datetime.now, description="The time the task was submitted."
)
started_at: datetime | None = Field(
default=None, description="The time the task was started."
)
completed_at: datetime | None = Field(
default=None, description="The time the task was completed."
)
error: str | None = Field(
default=None, description="The error message if the task failed."
)
These models ensure that the data exchanged between the client and the server is well-defined and validated.
Database
In this section, we will implement a database proxy to store the tasks and solutions. For simplicity, we use Redis, which serves as both our database and task queue. This approach minimizes the need to set up additional databases and leverages Redis’s key-value storage and automatic data expiration features.
The TspJobDbConnection class encapsulates the interactions with the Redis
database. It provides methods to register new jobs, update job statuses,
retrieve job requests, statuses, and solutions, list all jobs, and delete jobs.
# ./app/db.py
"""
This file contains a proxy class to interact with the database.
We are using Redis as the database for this example, but the implementation
can be easily adapted to other databases, as the proxy class abstracts the
database operations.
"""
import json
from models import TspJobStatus, TspJobRequest
from solver import TspSolution
from uuid import UUID
import redis
from typing import Optional, List
import logging
The class is initialized with a Redis client and an expiration time for the
stored data. The _get_data method is a helper that retrieves and parses JSON
data from Redis by key.
class TspJobDbConnection:
def __init__(self, redis_client: redis.Redis, expire_time: int = 24 * 60 * 60):
"""Initialize the Redis connection and expiration time."""
self._redis = redis_client
self._expire_time = expire_time
logging.basicConfig(level=logging.INFO)
def _get_data(self, key: str) -> Optional[dict]:
"""Get data from Redis by key and parse JSON."""
try:
data = self._redis.get(key)
if data is not None:
return json.loads(data)
except redis.RedisError as e:
logging.error(f"Redis error: {e}")
return None
The get_request, get_status, and get_solution methods retrieve a TSP job
request, status, and solution, respectively, by their task ID.
def get_request(self, task_id: UUID) -> Optional[TspJobRequest]:
"""Retrieve a TSP job request by task ID."""
data = self._get_data(f"request:{task_id}")
return TspJobRequest(**data) if data else None
def get_status(self, task_id: UUID) -> Optional[TspJobStatus]:
"""Retrieve a TSP job status by task ID."""
data = self._get_data(f"status:{task_id}")
return TspJobStatus(**data) if data else None
def get_solution(self, task_id: UUID) -> Optional[TspSolution]:
"""Retrieve a TSP solution by task ID."""
data = self._get_data(f"solution:{task_id}")
return TspSolution(**data) if data else None
The set_solution method stores a TSP solution in Redis with an expiration
time. The register_job method registers a new TSP job request and status in
Redis.
def set_solution(self, task_id: UUID, solution: TspSolution) -> None:
"""Set a TSP solution in Redis with an expiration time."""
try:
self._redis.set(
f"solution:{task_id}", solution.model_dump_json(), ex=self._expire_time
)
except redis.RedisError as e:
logging.error("Redis error: %s", e)
def register_job(self, request: TspJobRequest) -> TspJobStatus:
"""Register a new TSP job request and status in Redis."""
job_status = TspJobStatus()
try:
pipeline = self._redis.pipeline()
pipeline.set(
f"status:{job_status.task_id}",
job_status.model_dump_json(),
ex=self._expire_time,
)
pipeline.set(
f"request:{job_status.task_id}",
request.model_dump_json(),
ex=self._expire_time,
)
pipeline.execute()
except redis.RedisError as e:
logging.error("Redis error: %s", e)
return job_status
The update_job_status method updates the status of an existing TSP job. The
list_jobs method lists all TSP job statuses.
def update_job_status(self, job_status: TspJobStatus) -> None:
"""Update the status of an existing TSP job."""
try:
self._redis.set(
f"status:{job_status.task_id}",
job_status.model_dump_json(),
ex=self._expire_time,
)
except redis.RedisError as e:
logging.error("Redis error: %s", e)
def list_jobs(self) -> List[TspJobStatus]:
"""List all TSP job statuses."""
try:
status_keys = self._redis.keys("status:*")
data = self._redis.mget(status_keys)
return [TspJobStatus(**json.loads(status)) for status in data if status]
except redis.RedisError as e:
logging.error("Redis error: %s", e)
return []
The delete_job method deletes a TSP job request, status, and solution from
Redis.
def delete_job(self, task_id: UUID) -> None:
"""Delete a TSP job request, status, and solution from Redis."""
try:
pipeline = self._redis.pipeline()
pipeline.delete(f"status:{task_id}")
pipeline.delete(f"request:{task_id}")
pipeline.delete(f"solution:{task_id}")
pipeline.execute()
except redis.RedisError as e:
logging.error("Redis error: %s", e)
Configuration
The database and task queue require a connection to be established before they
can be used. We provide get_db_connection and get_task_queue functions in
the config.py file for three primary reasons:
- To ensure that the database and task queue are properly set up with the correct connection details. If we change the Redis host, we only need to update it in one place.
- To integrate these functions into FastAPI’s dependency injection system, ensuring that the database and task queue are available to the API endpoints without establishing the connection in each endpoint. This approach also facilitates testing with a different database.
- To allow both the FastAPI application and the workers to use the same configuration functions, despite having different entry points.
# ./app/config.py
"""
This file contains the configuration for the optimization API.
For this simple project, it only sets up the database connection and the task queue.
The other parts of the API should not be aware of the specific connection details.
"""
from db import TspJobDbConnection
import redis
from rq import Queue
def get_db_connection() -> TspJobDbConnection:
"""Provides a TspJobDbConnection instance."""
redis_client = redis.Redis(
host="optimization_api_redis", port=6379, decode_responses=True, db=0
)
return TspJobDbConnection(redis_client=redis_client)
def get_task_queue() -> Queue:
"""Provides a Redis Queue instance."""
redis_client = redis.Redis(host="optimization_api_redis", port=6379, db=1)
return Queue(connection=redis_client)
Tasks
With the database in place, we can create the tasks that will run the
optimization. The optimization will run in a separate process and use the
database to communicate with the web server. To keep things simple, we will pass
only the job reference to the task. The task will fetch the necessary data from
the database and update the database with the results. Additionally, by
including an if __name__ == "__main__": block, we allow the tasks to be run
via an external task queue as system commands.
The tasks.py file contains functions and logic for running the optimization
job in a separate worker process.
# ./app/tasks.py
"""
This file is responsible for running the optimization job in a separate worker.
"""
from config import get_db_connection
from models import TspJobRequest, TspJobStatus
from solver import TspSolver
from datetime import datetime
from uuid import UUID
from db import TspJobDbConnection
import httpx
import logging
The send_webhook function sends a POST request to the specified webhook URL
with the job status. This allows for asynchronous notifications when the
computation is complete.
def send_webhook(job_request: TspJobRequest, job_status: TspJobStatus) -> None:
if job_request.webhook_url:
try:
# Send a POST request to the webhook URL
response = httpx.post(
url=f"{job_request.webhook_url}", json=job_status.model_dump_json()
)
response.raise_for_status() # Raise an error for bad responses
except httpx.HTTPStatusError as e:
logging.error(
f"HTTP error occurred: {e.response.status_code} - {e.response.text}"
)
except Exception as e:
logging.error(f"An error occurred: {e}")
The run_optimization_job function fetches the job request from the database,
runs the optimization algorithm, and stores the solution back in the database.
It also updates the job status and sends a webhook notification upon completion.
def run_optimization_job(
job_id: UUID, db_connection: TspJobDbConnection | None = None
) -> None:
"""
Will fetch the job request from the database, run the optimization algorithm,
and store the solution back in the database. Finally, it will send a webhook
to the URL specified in the job. This function may be run on a separate worker,
which is why we do not pass or return data directly, but rather use the database.
"""
if db_connection is None:
db_connection = get_db_connection()
job_status = db_connection.get_status(job_id)
job_request = db_connection.get_request(job_id)
if job_status is None or job_request is None:
return # job got deleted
job_status.status = "Running"
job_status.started_at = datetime.now()
db_connection.update_job_status(job_status)
solver = TspSolver(job_request.tsp_instance, job_request.optimization_parameters)
solution = solver.solve(log_callback=print)
db_connection.set_solution(job_id, solution)
job_status.status = "Completed"
job_status.completed_at = datetime.now()
db_connection.update_job_status(job_status)
send_webhook(job_request, job_status)
API
In this final section, we will build the actual API using FastAPI. This API will expose endpoints to submit TSP job requests, check job statuses, retrieve solutions, cancel jobs, and list all jobs. FastAPI provides an efficient and easy-to-use framework for building web APIs with Python.
The main.py file contains the FastAPI application setup and the API routes.
For simplicity, all routes are included in a single file, but in larger
projects, it is advisable to separate them into different modules.
# ./app/main.py
"""
This file contains the main FastAPI application.
For a larger project, we would move the routes to separate files, but for this example, we keep everything in one file.
"""
from uuid import UUID
from fastapi import FastAPI, APIRouter, HTTPException, Depends
from models import TspJobRequest, TspJobStatus
from solver import TspSolution
from config import get_db_connection, get_task_queue
from tasks import run_optimization_job
The FastAPI application is initialized with a title and description. An API router is created to group the routes related to the TSP solver.
app = FastAPI(
title="My Optimization API",
description="This is an example on how to deploy an optimization algorithm based on CP-SAT as an API.",
)
tsp_solver_v1_router = APIRouter(tags=["TSP_solver_v1"])
The post_job endpoint allows users to submit a new TSP job. The job is
registered in the database, and the optimization task is enqueued in the task
queue for asynchronous processing.
@tsp_solver_v1_router.post("/jobs", response_model=TspJobStatus)
def post_job(
job_request: TspJobRequest,
db_connection=Depends(get_db_connection),
task_queue=Depends(get_task_queue),
):
"""
Submit a new job to solve a TSP instance.
"""
job_status = db_connection.register_job(job_request)
# enqueue the optimization job in the task queue.
# Will return immediately, the job will be run in a separate worker.
task_queue.enqueue(
run_optimization_job,
job_status.task_id,
# adding a 60 second buffer to the job timeout
job_timeout=job_request.optimization_parameters.timeout + 60,
)
return job_status
The get_job endpoint returns the status of a specific job identified by its
task ID.
@tsp_solver_v1_router.get("/jobs/{task_id}", response_model=TspJobStatus)
def get_job(task_id: UUID, db_connection=Depends(get_db_connection)):
"""
Return the status of a job.
"""
status = db_connection.get_status(task_id)
if status is None:
raise HTTPException(status_code=404, detail="Job not found")
return status
The get_solution endpoint returns the solution of a specific job if it is
available.
@tsp_solver_v1_router.get("/jobs/{task_id}/solution", response_model=TspSolution)
def get_solution(task_id: UUID, db_connection=Depends(get_db_connection)):
"""
Return the solution of a job, if available.
"""
solution = db_connection.get_solution(task_id)
if solution is None:
raise HTTPException(status_code=404, detail="Solution not found")
return solution
The cancel_job endpoint deletes or cancels a job. It does not immediately stop
the job if it is already running.
@tsp_solver_v1_router.delete("/jobs/{task_id}")
def cancel_job(task_id: UUID, db_connection=Depends(get_db_connection)):
"""
Deletes/cancels a job. This will *not* immediately stop the job if it is running.
"""
db_connection.delete_job(task_id)
The list_jobs endpoint returns a list of all jobs and their statuses.
@tsp_solver_v1_router.get("/jobs", response_model=list[TspJobStatus])
def list_jobs(db_connection=Depends(get_db_connection)):
"""
List all jobs.
"""
return db_connection.list_jobs()
Finally, we include the API router in the FastAPI application under the
/tsp_solver/v1 prefix.
app.include_router(tsp_solver_v1_router, prefix="/tsp_solver/v1")
Running the Application
After you have run docker-compose up -d --build, you can access the API at
http://localhost:80/docs. This will open the Swagger UI, where you can test
the API. You can submit a job, check the status, and retrieve the solution. You
can also cancel a job or list all jobs.
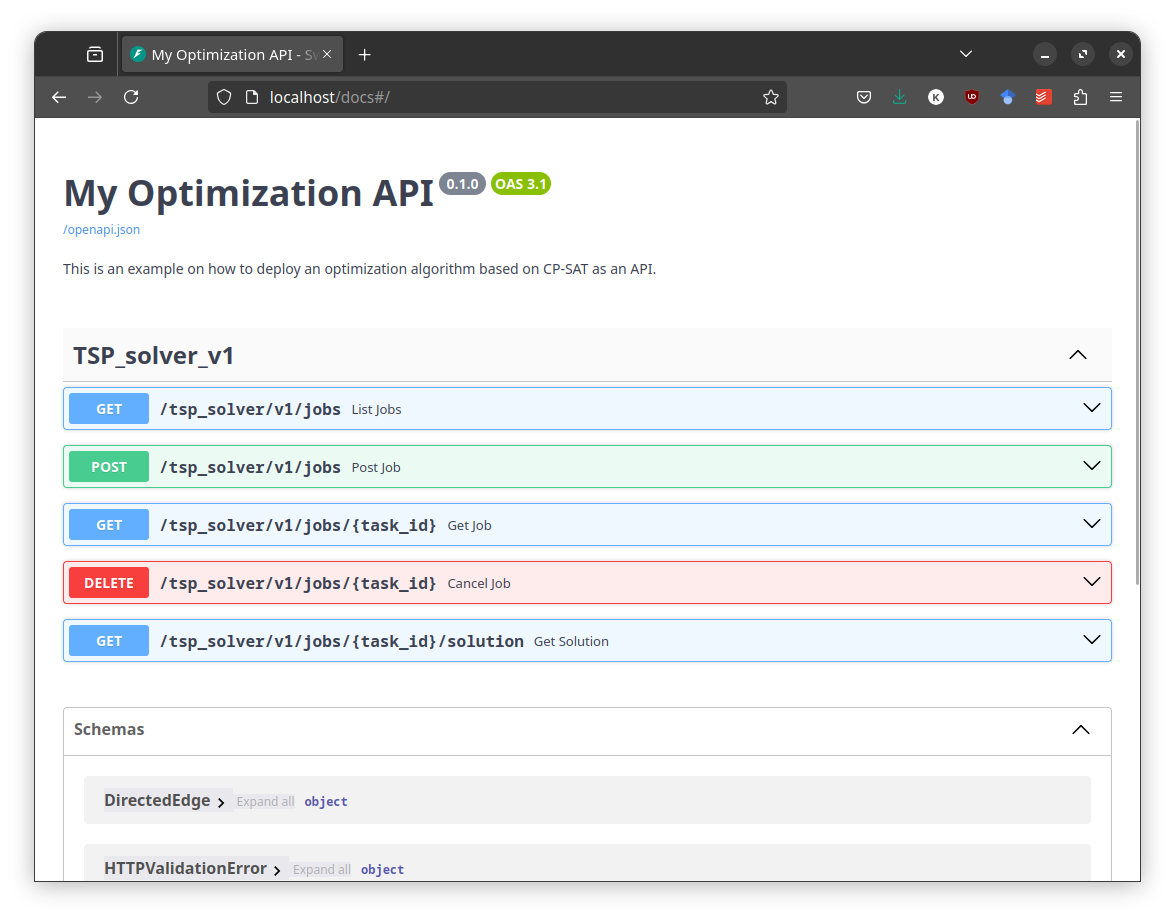 |
|---|
| FastAPI comes with a built-in Swagger UI that allows you to interact with the API. |
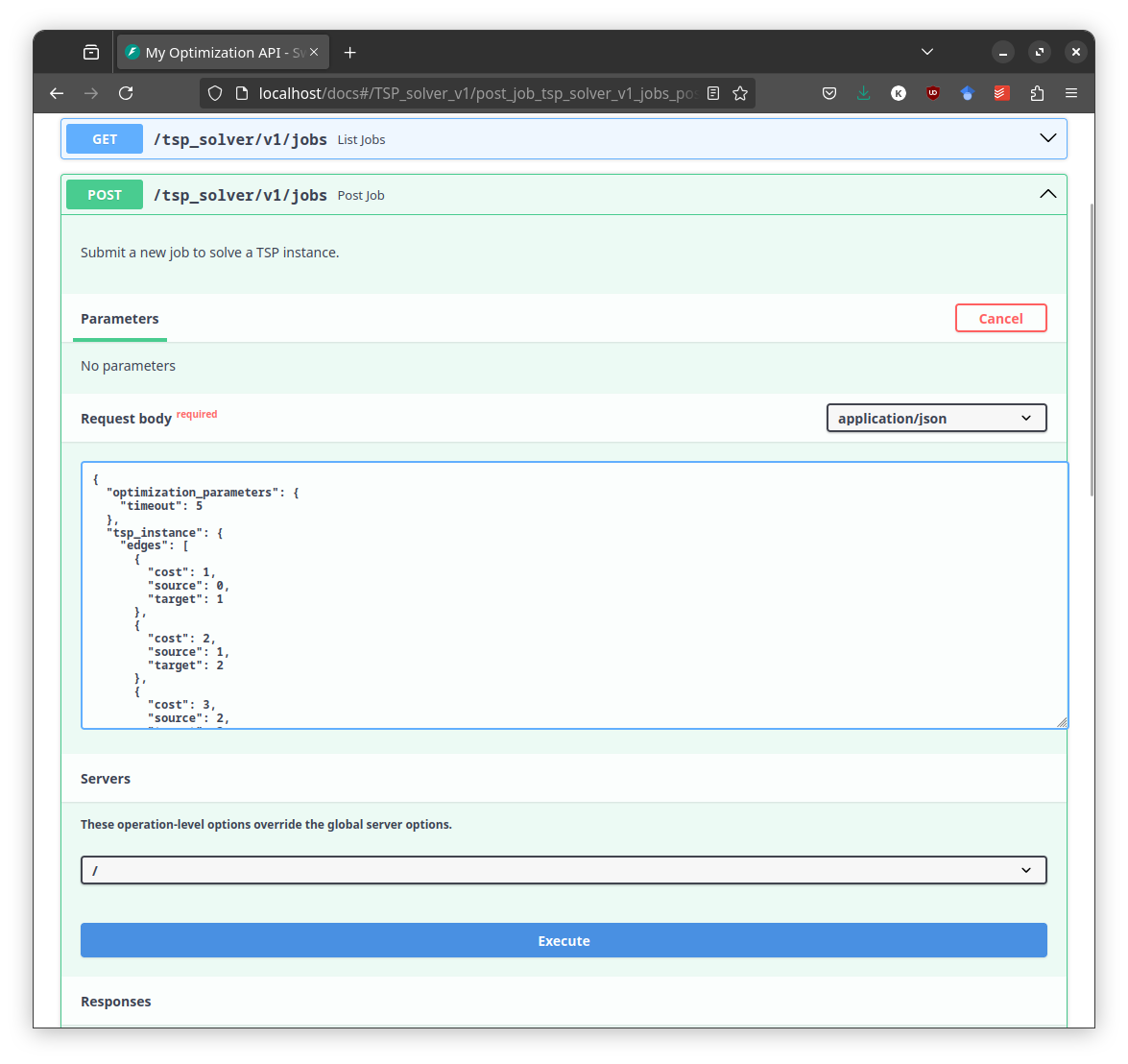 |
|---|
| By clicking on “try it out” you can directly submit a job to the API. |
Here is an instance to try it out: (click to expand)
{
"optimization_parameters": {
"timeout": 5
},
"tsp_instance": {
"num_nodes": 15,
"edges": [
{ "source": 0, "target": 1, "cost": 82 },
{ "source": 1, "target": 0, "cost": 82 },
{ "source": 0, "target": 2, "cost": 35 },
{ "source": 2, "target": 0, "cost": 35 },
{ "source": 0, "target": 3, "cost": 58 },
{ "source": 3, "target": 0, "cost": 58 },
{ "source": 0, "target": 4, "cost": 9 },
{ "source": 4, "target": 0, "cost": 9 },
{ "source": 0, "target": 5, "cost": 13 },
{ "source": 5, "target": 0, "cost": 13 },
{ "source": 0, "target": 6, "cost": 91 },
{ "source": 6, "target": 0, "cost": 91 },
{ "source": 0, "target": 7, "cost": 72 },
{ "source": 7, "target": 0, "cost": 72 },
{ "source": 0, "target": 8, "cost": 16 },
{ "source": 8, "target": 0, "cost": 16 },
{ "source": 0, "target": 9, "cost": 50 },
{ "source": 9, "target": 0, "cost": 50 },
{ "source": 0, "target": 10, "cost": 80 },
{ "source": 10, "target": 0, "cost": 80 },
{ "source": 0, "target": 11, "cost": 92 },
{ "source": 11, "target": 0, "cost": 92 },
{ "source": 0, "target": 12, "cost": 28 },
{ "source": 12, "target": 0, "cost": 28 },
{ "source": 0, "target": 13, "cost": 17 },
{ "source": 13, "target": 0, "cost": 17 },
{ "source": 0, "target": 14, "cost": 97 },
{ "source": 14, "target": 0, "cost": 97 },
{ "source": 1, "target": 2, "cost": 14 },
{ "source": 2, "target": 1, "cost": 14 },
{ "source": 1, "target": 3, "cost": 32 },
{ "source": 3, "target": 1, "cost": 32 },
{ "source": 1, "target": 4, "cost": 41 },
{ "source": 4, "target": 1, "cost": 41 },
{ "source": 1, "target": 5, "cost": 52 },
{ "source": 5, "target": 1, "cost": 52 },
{ "source": 1, "target": 6, "cost": 58 },
{ "source": 6, "target": 1, "cost": 58 },
{ "source": 1, "target": 7, "cost": 20 },
{ "source": 7, "target": 1, "cost": 20 },
{ "source": 1, "target": 8, "cost": 1 },
{ "source": 8, "target": 1, "cost": 1 },
{ "source": 1, "target": 9, "cost": 54 },
{ "source": 9, "target": 1, "cost": 54 },
{ "source": 1, "target": 10, "cost": 75 },
{ "source": 10, "target": 1, "cost": 75 },
{ "source": 1, "target": 11, "cost": 15 },
{ "source": 11, "target": 1, "cost": 15 },
{ "source": 1, "target": 12, "cost": 45 },
{ "source": 12, "target": 1, "cost": 45 },
{ "source": 1, "target": 13, "cost": 94 },
{ "source": 13, "target": 1, "cost": 94 },
{ "source": 1, "target": 14, "cost": 41 },
{ "source": 14, "target": 1, "cost": 41 },
{ "source": 2, "target": 3, "cost": 82 },
{ "source": 3, "target": 2, "cost": 82 },
{ "source": 2, "target": 4, "cost": 44 },
{ "source": 4, "target": 2, "cost": 44 },
{ "source": 2, "target": 5, "cost": 83 },
{ "source": 5, "target": 2, "cost": 83 },
{ "source": 2, "target": 6, "cost": 91 },
{ "source": 6, "target": 2, "cost": 91 },
{ "source": 2, "target": 7, "cost": 78 },
{ "source": 7, "target": 2, "cost": 78 },
{ "source": 2, "target": 8, "cost": 51 },
{ "source": 8, "target": 2, "cost": 51 },
{ "source": 2, "target": 9, "cost": 6 },
{ "source": 9, "target": 2, "cost": 6 },
{ "source": 2, "target": 10, "cost": 81 },
{ "source": 10, "target": 2, "cost": 81 },
{ "source": 2, "target": 11, "cost": 77 },
{ "source": 11, "target": 2, "cost": 77 },
{ "source": 2, "target": 12, "cost": 93 },
{ "source": 12, "target": 2, "cost": 93 },
{ "source": 2, "target": 13, "cost": 97 },
{ "source": 13, "target": 2, "cost": 97 },
{ "source": 2, "target": 14, "cost": 33 },
{ "source": 14, "target": 2, "cost": 33 },
{ "source": 3, "target": 4, "cost": 66 },
{ "source": 4, "target": 3, "cost": 66 },
{ "source": 3, "target": 5, "cost": 47 },
{ "source": 5, "target": 3, "cost": 47 },
{ "source": 3, "target": 6, "cost": 54 },
{ "source": 6, "target": 3, "cost": 54 },
{ "source": 3, "target": 7, "cost": 39 },
{ "source": 7, "target": 3, "cost": 39 },
{ "source": 3, "target": 8, "cost": 98 },
{ "source": 8, "target": 3, "cost": 98 },
{ "source": 3, "target": 9, "cost": 90 },
{ "source": 9, "target": 3, "cost": 90 },
{ "source": 3, "target": 10, "cost": 5 },
{ "source": 10, "target": 3, "cost": 5 },
{ "source": 3, "target": 11, "cost": 27 },
{ "source": 11, "target": 3, "cost": 27 },
{ "source": 3, "target": 12, "cost": 61 },
{ "source": 12, "target": 3, "cost": 61 },
{ "source": 3, "target": 13, "cost": 95 },
{ "source": 13, "target": 3, "cost": 95 },
{ "source": 3, "target": 14, "cost": 19 },
{ "source": 14, "target": 3, "cost": 19 },
{ "source": 4, "target": 5, "cost": 34 },
{ "source": 5, "target": 4, "cost": 34 },
{ "source": 4, "target": 6, "cost": 10 },
{ "source": 6, "target": 4, "cost": 10 },
{ "source": 4, "target": 7, "cost": 20 },
{ "source": 7, "target": 4, "cost": 20 },
{ "source": 4, "target": 8, "cost": 44 },
{ "source": 8, "target": 4, "cost": 44 },
{ "source": 4, "target": 9, "cost": 33 },
{ "source": 9, "target": 4, "cost": 33 },
{ "source": 4, "target": 10, "cost": 29 },
{ "source": 10, "target": 4, "cost": 29 },
{ "source": 4, "target": 11, "cost": 36 },
{ "source": 11, "target": 4, "cost": 36 },
{ "source": 4, "target": 12, "cost": 62 },
{ "source": 12, "target": 4, "cost": 62 },
{ "source": 4, "target": 13, "cost": 77 },
{ "source": 13, "target": 4, "cost": 77 },
{ "source": 4, "target": 14, "cost": 63 },
{ "source": 14, "target": 4, "cost": 63 },
{ "source": 5, "target": 6, "cost": 73 },
{ "source": 6, "target": 5, "cost": 73 },
{ "source": 5, "target": 7, "cost": 6 },
{ "source": 7, "target": 5, "cost": 6 },
{ "source": 5, "target": 8, "cost": 91 },
{ "source": 8, "target": 5, "cost": 91 },
{ "source": 5, "target": 9, "cost": 5 },
{ "source": 9, "target": 5, "cost": 5 },
{ "source": 5, "target": 10, "cost": 61 },
{ "source": 10, "target": 5, "cost": 61 },
{ "source": 5, "target": 11, "cost": 11 },
{ "source": 11, "target": 5, "cost": 11 },
{ "source": 5, "target": 12, "cost": 91 },
{ "source": 12, "target": 5, "cost": 91 },
{ "source": 5, "target": 13, "cost": 7 },
{ "source": 13, "target": 5, "cost": 7 },
{ "source": 5, "target": 14, "cost": 88 },
{ "source": 14, "target": 5, "cost": 88 },
{ "source": 6, "target": 7, "cost": 52 },
{ "source": 7, "target": 6, "cost": 52 },
{ "source": 6, "target": 8, "cost": 86 },
{ "source": 8, "target": 6, "cost": 86 },
{ "source": 6, "target": 9, "cost": 48 },
{ "source": 9, "target": 6, "cost": 48 },
{ "source": 6, "target": 10, "cost": 13 },
{ "source": 10, "target": 6, "cost": 13 },
{ "source": 6, "target": 11, "cost": 31 },
{ "source": 11, "target": 6, "cost": 31 },
{ "source": 6, "target": 12, "cost": 91 },
{ "source": 12, "target": 6, "cost": 91 },
{ "source": 6, "target": 13, "cost": 62 },
{ "source": 13, "target": 6, "cost": 62 },
{ "source": 6, "target": 14, "cost": 30 },
{ "source": 14, "target": 6, "cost": 30 },
{ "source": 7, "target": 8, "cost": 79 },
{ "source": 8, "target": 7, "cost": 79 },
{ "source": 7, "target": 9, "cost": 94 },
{ "source": 9, "target": 7, "cost": 94 },
{ "source": 7, "target": 10, "cost": 58 },
{ "source": 10, "target": 7, "cost": 58 },
{ "source": 7, "target": 11, "cost": 12 },
{ "source": 11, "target": 7, "cost": 12 },
{ "source": 7, "target": 12, "cost": 81 },
{ "source": 12, "target": 7, "cost": 81 },
{ "source": 7, "target": 13, "cost": 2 },
{ "source": 13, "target": 7, "cost": 2 },
{ "source": 7, "target": 14, "cost": 89 },
{ "source": 14, "target": 7, "cost": 89 },
{ "source": 8, "target": 9, "cost": 15 },
{ "source": 9, "target": 8, "cost": 15 },
{ "source": 8, "target": 10, "cost": 94 },
{ "source": 10, "target": 8, "cost": 94 },
{ "source": 8, "target": 11, "cost": 23 },
{ "source": 11, "target": 8, "cost": 23 },
{ "source": 8, "target": 12, "cost": 50 },
{ "source": 12, "target": 8, "cost": 50 },
{ "source": 8, "target": 13, "cost": 79 },
{ "source": 13, "target": 8, "cost": 79 },
{ "source": 8, "target": 14, "cost": 65 },
{ "source": 14, "target": 8, "cost": 65 },
{ "source": 9, "target": 10, "cost": 68 },
{ "source": 10, "target": 9, "cost": 68 },
{ "source": 9, "target": 11, "cost": 81 },
{ "source": 11, "target": 9, "cost": 81 },
{ "source": 9, "target": 12, "cost": 34 },
{ "source": 12, "target": 9, "cost": 34 },
{ "source": 9, "target": 13, "cost": 21 },
{ "source": 13, "target": 9, "cost": 21 },
{ "source": 9, "target": 14, "cost": 16 },
{ "source": 14, "target": 9, "cost": 16 },
{ "source": 10, "target": 11, "cost": 10 },
{ "source": 11, "target": 10, "cost": 10 },
{ "source": 10, "target": 12, "cost": 12 },
{ "source": 12, "target": 10, "cost": 12 },
{ "source": 10, "target": 13, "cost": 60 },
{ "source": 13, "target": 10, "cost": 60 },
{ "source": 10, "target": 14, "cost": 61 },
{ "source": 14, "target": 10, "cost": 61 },
{ "source": 11, "target": 12, "cost": 36 },
{ "source": 12, "target": 11, "cost": 36 },
{ "source": 11, "target": 13, "cost": 78 },
{ "source": 13, "target": 11, "cost": 78 },
{ "source": 11, "target": 14, "cost": 79 },
{ "source": 14, "target": 11, "cost": 79 },
{ "source": 12, "target": 13, "cost": 54 },
{ "source": 13, "target": 12, "cost": 54 },
{ "source": 12, "target": 14, "cost": 33 },
{ "source": 14, "target": 12, "cost": 33 },
{ "source": 13, "target": 14, "cost": 29 },
{ "source": 14, "target": 13, "cost": 29 }
]
}
}
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
CP-SAT vs. ML vs. QC
Classical Optimization vs. Machine Learning (and the impact of Quantum Computing)
A prevalent discussion in today’s landscape revolves around whether Machine Learning (ML) or Quantum Computing (QC) could replace classical optimization methods such as CP-SAT. In this chapter, we will explore the fundamental differences between Machine Learning and Optimization, demonstrating that these fields are not interchangeable but rather complementary to each other. By understanding their distinct strengths and applications, we can better leverage each approach to solve complex problems effectively.
Following our discussion on these differences, a common question arises: will Quantum Computing render classical optimization techniques obsolete? To address this, we will delve into the basic challenges facing Quantum Computing in the context of Optimization and explain why its impact may be less significant than often anticipated. This section aims to debunk several myths, some of which are perpetuated by proponents of Quantum Computing.
Machine Learning excels at predicting outcomes based on historical data, identifying patterns, and making informed guesses, such as estimating the best solution to an optimization problem based on data patterns. It is adept at learning and generalizing from data, even if the data is imperfect, provided there is sufficient quantity. On the other hand, Optimization is powerful for systematically searching for the best solution based on a well-defined mathematical model, capable of optimizing variables and constraints with precision, often requiring minimal data. For example, in planning delivery routes, ML can predict driving times and resource needs based on historical factors, whereas an optimization solver like CP-SAT is better suited to determining the most efficient routes by evaluating the interdependencies and constraints systematically. Both fields enhance decision-making processes when used together, leveraging ML’s predictive capabilities and Optimization’s rigorous solution-finding methods.
In the article Four Key Differences Between Mathematical Optimization And Machine Learning, Edward Rothberg, the CEO of Gurobi, highlights four key differences between Machine Learning and Optimization:
- Analytical Focus: ML is primarily a predictive tool that identifies patterns in historical data to forecast future events, whereas Optimization is a prescriptive tool that uses a digital twin of your environment to recommend the best possible decisions.
- Typical Applications: ML is commonly used for tasks like fraud detection, speech recognition, and product recommendations—often consumer-facing applications. Optimization is leveraged for operational decision-making in areas like production planning, scheduling, and shipment routing.
- Adaptability: ML can suffer from “model drift” if the environment changes significantly, requiring retraining with new data. Optimization models, however, can be updated more seamlessly to reflect changes in real time but usually need more upfront effort to build.
- Maturity: Both fields have roots tracing back decades, but Optimization has largely settled into a “plateau of productivity,” while ML is currently at the “peak of inflated expectations” and may face a phase of disillusionment before stabilizing into broader adoption.
 You do not have to read this section if you are not interested in my arguments. The TL;DR is that neither Machine Learning nor Quantum Computing will make CP-SAT (and similar methods) obsolete any time soon, if ever. However, Machine Learning is a valuable complement to Optimization. |
|
ML ain’t your only hammer: adding mathematical optimisation to the data scientist’s toolbox: This 20-minute talk by Dr. Jack Simpson introduces data scientists with a machine learning focus to mathematical optimization, highlighting how it prescribes optimal decisions under complex constraints and complements ML forecasts.  |
Using GenAI/LLMs for Optimization
It is indeed possible to ask ChatGPT (or similar large language models) to solve certain optimization problems, and in simpler cases (like the Knapsack Problem) it often succeeds by automatically writing Python code that calls an external solver (e.g., HiGHs). Although this approach may work for small instances, it generally runs much slower than a dedicated solver and can introduce subtle errors. In the example below, ChatGPT took around 10 seconds, whereas a specialized solver would have solved the same instance almost instantly:
 |  |
|---|---|
| Asking ChatGPT to solve a Knapsack Problem, which it does successfully… | …but under the hood, it relies on an external solver. |
More advanced versions of ChatGPT (e.g., ChatGPT 4) can tackle somewhat larger problems but still fall short of solvers like CP-SAT that systematically evaluate massive search spaces with efficient backtracking and pruning. Large language models process information sequentially in short “turns”, have limited context windows, and lack specialized heuristics - factors that make them prone to logical missteps and slower performance as the problem size grows. Repeatedly generating code or text also creates overhead, and verifying solutions can require multiple iterations of prompting, further compounding the time cost.
Because of these limitations, LLMs are unlikely to replace robust solvers for substantial or complex optimization tasks anytime soon. However, current research on hybrid AI-OR methods aims to combine the flexibility of LLMs (such as quick prototyping and model building) with the powerful search capabilities of dedicated solvers. As this field evolves, LLMs may increasingly assist in formulating or refining optimization models while specialized engines focus on the computationally intensive search. We will revisit these possibilities in the upcoming section on “Model Building with GenAI/LLMs”.
To dig a little deeper into the limitations of LLMs for optimization, consider the following articles:
- LLM-ify me - Optimization edition: A blog post exploring the potential of LLMs for optimization.
- Mind Evolution and the frontier of LLM-based optimization solvers: An article from the Feasible newsletter discussing the potential of LLMs for optimization.
- Why Solving Multi-agent Path Finding with Large Language Models has not Succeeded Yet
- Look Further Ahead: Testing the Limits of GPT-4 in Path Planning
- Extracting Problem Structure with LLMs for Optimized SAT Local Search: This paper demonstrates how an LLM can be used to automatically generate start heuristics from Python code that models a problem as a SAT instance using the PySAT library. These start heuristics provide the initial phase for a SAT solver, helping it begin the search from a more promising assignment and enabling it to solve additional instances that would remain unsolved otherwise.
Reinforcement Learning
In some cases, an actually viable alternative to optimization solvers like CP-SAT is Reinforcement Learning. Reinforcement learning can be highly effective for optimizing very complex problems that are too intricate to model with simple mathematical formulations. During my dissertation, I applied reinforcement learning to optimize a multi-agent system where developing a comprehensive mathematical model was infeasible due to the excessive number of variables and constraints required to capture the system’s dynamics. Additionally, manually crafted heuristics proved unable to compete with the performance of a straightforward reinforcement learning agent, which I implemented with minimal effort using Stable Baselines. However, despite reinforcement learning agents being capable of performing many more iterations to learn about the solution space compared to large language models (LLMs), they still lack the structured and efficient search capabilities inherent in classical solvers. Furthermore, designing an appropriate reward function for reinforcement learning can be challenging and often involves significant trial and error.
Combining Machine Learning and Optimization
Instead of trying to replace optimization solvers like CP-SAT with machine learning, a more promising approach is to combine the two fields. This can be achieved in several ways, such as using machine learning to predict parameters for optimization problems, building optimization proxies, or integrating machine learning within solvers to guide internal decisions. These methods leverage the strengths of both fields to enhance decision-making processes and improve solution quality.
Predict-Then-Optimize Variants
Predict-Then-Optimize is a framework that combines machine learning with optimization. The basic version involves two simple steps: predict and then optimize. First, a standard ML model (e.g., a regression) is trained to estimate unknown parameters of the optimization problem, such as costs or demands, using conventional loss functions like mean squared error. Next, these predicted parameters are passed to an optimization solver (such as CP-SAT), which produces a best-possible solution—say, a schedule, route, or resource allocation—based on the estimated inputs. This approach is effective when the model’s predictive accuracy is reasonably high, but it can falter if small errors in the predictions cause large downstream impacts on the decision.
To improve decision quality, more advanced, “decision-focused” variants of Predict-Then-Optimize incorporate the solver’s objective directly into the ML training process. Rather than merely minimizing standard predictive error, these methods seek to minimize “regret”—the gap between the cost of the solver’s solution under predicted parameters and the cost of the true optimal solution. By repeatedly using the solver (or an approximation) during training, they compute how prediction mistakes translate into suboptimal decisions, and feed this information back to the ML model’s parameters. As a result, the model learns to predict in a way that preserves or improves the final solution’s quality, even if the raw predictive accuracy on each parameter is not perfectly precise.
Check out this great lecture by Elias Khalil which was part of a summer school.
 Uncertainty and unknown parameters frequently arise in optimization problems. While the predict-then-optimize framework offers a straightforward approach, its more advanced variants can help address some of its limitations. For even greater robustness, techniques such as robust optimization, stochastic programming, and others provide more effective solutions, especially in highly uncertain environments, though they come with increased complexity. Numerous research studies explore these and additional methods, with the optimal choice depending heavily on the specific application. |
Optimization Proxies
An optimization proxy is a machine learning model trained to approximate the input-output behavior of an optimization solver, enabling near-instant decisions once deployed. Typically, one gathers a large set of problem instances, solves them offline using a traditional solver to generate “ground truth” solutions, and then trains an ML model to map inputs (e.g., demands, costs) to outputs (the solver’s decisions). In real-time or large-scale simulation settings—such as power systems, scheduling, or routing—using the learned proxy bypasses the usual heavy solve times, providing solutions (or near-solutions) almost instantly. Because the training data comes directly from the solver, no manual labeling is required; any number of instances can be generated offline.
However, optimization proxies excel only when repeatedly solving relatively similar models under stable conditions, and they can struggle when complex feasibility constraints or drastically changing problem parameters arise. Though they have found very useful applications in areas like power networks, many other optimization contexts involve too many shifting variables or intricate constraints for a simple proxy to handle reliably. Substantial changes to the problem’s structure often require retraining or extensive model adaptation. As a result, while proxies can be a powerful add-on to speed up certain classes of problem instances, they are by no means a universal replacement for classical solvers.
A short 4min explanation is given by Pascal Van Hentenryck. And a longer version can be found here.
Model Building with GenAI/LLMs
An increasingly valuable application of LLMs (or generative AI) in optimization is assisting with the model building process. Rather than trying to solve an optimization problem directly, which is often ineffective, these models can help set up the initial model that a specialized solver will handle. Many optimization models share similar structures and differ only in certain details, making LLMs useful for producing core components. Tools like GitHub Co-Pilot can already generate complex parts of a model, yet they may also introduce subtle errors that are hard to detect, such as off by one mistakes, inverted constraints, or swapped indices. It is therefore best to use LLMs as a source of inspiration and verify their output carefully; otherwise, the time you save coding might be spent on debugging.
Moreover, your optimization model often represents the backbone of a real world problem, so it is crucial to understand how it aligns with the underlying operational or business context. While LLMs can expedite coding, they cannot replace the human expertise needed to approximate and simplify real world complexities. If the scenario is critical, you may not want to rely too heavily on an AI-based approach at this stage. That said, several research projects and commercial products are already exploring this idea:
- A Research Project at Stanford
- Gurobi AI Modeling (Quick Overview)
- Quantagonia provides a solver you can interact with via chat
- Robust and Adaptive Optimization under a Large Language Model Lens: A research paper exploring using LLMs for robust optimization.
- DualSchool: How Reliable are LLMs for Optimization Education?: This paper shows that LLMs still struggle with simple, recipe-based tasks like dualizing linear programs.
Learning instead of Guessing
Machine learning can also be integrated inside solvers, guiding internal decisions such as branching strategies, cut selection, or matrix scaling. Rather than relying on hand-tuned rules alone, the solver gathers data across diverse problem instances and learns which algorithmic choices best reduce run time or improve numerical stability. For instance, a model can predict whether “local” or “global” cutting planes will be more effective on a given instance, or whether certain scaling methods will avoid ill-conditioned bases. By treating these decisions as regression tasks - estimating speedup or stability improvements - machine learning lets the solver adapt and self-tune, ultimately performing better on a wide spectrum of problems without sacrificing generality.
This lecture by Timo Berthold (FICO) gives a good overview of the topic. It has been part of the CO@Work 2024 summer school, which I actually attended and consider to be absolutely amazing and if you get the chance to attend, I highly recommend it (as long as you already are on PhD-level, as it is intense).
A three-hour tutorial by various experts on the topic (including Elias Khalil and Andrea Lodi), can be found here. I highly recommend watching it, if you are interested in the topic as I had many “aha” moments during this tutorial.

|
Why Quantum Computing Will (Probably) Not Have a Big Impact on Optimization
Before closing this chapter, let us also discuss the impact of Quantum Computing on Optimization, as this is a question I am frequently asked, usually directly after having explained why ChatGPT cannot replace CP-SAT.
You often hear claims that quantum computing will revolutionize optimization, especially regarding the Traveling Salesman Problem (TSP). These claims frequently state that a new quantum algorithm can solve TSP (a challenging yet practically important combinatorial optimization problem) for small instance sizes, while a classical computer would supposedly need billions of years to handle as few as 20 nodes. (In reality, some published papers still only address four nodes.) Unfortunately, such claims usually hinge on a theoretical worst-case runtime of around \( O(n^2 2^n) \) for the TSP, which is not representative of how the problem is handled in practice.
 For an accessible and insightful discussion on the myths and exaggerated expectations surrounding quantum computing, consult the freely available book What You Shouldn’t Know About Quantum Computers by Chris Ferrie. This resource offers an excellent opportunity to critically examine common misconceptions often perpetuated by science fiction and popular science literature. |
Although the best-known quantum algorithm runs in \( O(1.728^n) \), which is somewhat better than \( O(n^2 2^n) \), it remains exponential and grows very quickly. Since the TSP is NP-hard, it is unlikely we will ever discover a (quantum or classical) algorithm whose worst-case runtime does not explode with instance size. Moreover, real-world or average-case performance can be vastly different from worst-case performance. In fact, TSP can already be solved effectively for large instances on classical computers, so many bold claims about quantum computing’s purported advantages in optimization can be misleading or simply incorrect.
To date, there is no strong evidence suggesting that quantum computing will have a major impact on optimization. Many experts believe that, at best, quantum computing might offer only a modest performance advantage in this domain, though it may have significant implications for cryptology.
 At a recent consortium meeting, a consultant from a logistics optimization firm made a particularly noteworthy remark. According to them, even with the advent of a fully functional quantum computer equipped with thousands of flawless qubits, its primary utility would lie in marketing. Beyond that, it would be little more than “metal trash,” offering no tangible value for their customers’ use cases. This statement prompted humorous objections from quantum experts regarding the “metal trash” comment. Nevertheless, the broader sentiment that quantum computing is overhyped in the optimization domain was widely shared. |
To put the Traveling Salesman Problem’s difficulty into historical perspective: In the mid-20th century, the TSP attracted attention through challenges offering substantial prize money for solving relatively small instances of 33 to 49 cities - already far larger than those currently tackled by many quantum researchers. As Newsweek reported in 1954:
“By an ingenious application of linear programming - a mathematical tool recently used to solve production-scheduling problems - it took only a few weeks for the California experts to calculate by hand the shortest route to cover the 49 cities.”
Remarkably, they not only found the shortest route, but also proved it was the shortest, all by hand in the 1950s. You can read more details in this blog post. Nowadays, there is even an iPhone app that can solve instances of around 1,000 TSP cities to optimality in mere seconds. Larger-scale instances (up to 85,900 nodes, solved in 2006) and near-optimal solutions for millions of cities illustrate how far classical methods have come. In that sense, quantum computers have a considerable way to go before they can beat even a human with pen and paper, let alone a classical computer.
Misjudging the difficulty of certain combinatorial problems famously led one puzzle inventor into unexpected financial trouble. His creation, The Eternity Puzzle, offered a £1,000,000 prize to anyone who could solve it—a sum that some early estimates suggested might never be claimed in a human lifespan, given the vast number of possible configurations. However, instead of brute-forcing every possibility, two Cambridge mathematicians employed advanced techniques to dramatically narrow the search space. Similarly, CP-SAT leverages a variety of behind-the-scenes strategies to tackle complex problems more efficiently than most would imagine—indeed, many of the methods used to solve The Eternity Puzzle resemble what CP-SAT does in a more general way.
Thanks to these refined methods, the puzzle was solved in under 18 months - much sooner than anticipated. Although rumors circulated that the puzzle’s inventor, Christopher Monckton, was forced to sell his mansion to pay the prize, this appears to have been more of a publicity stunt; in reality, he could afford to cover the loss. He later released a successor puzzle, which has proven far more difficult and remains unsolved.
Quantum computers exploit superposition and entanglement to evaluate multiple solutions in parallel. However, they do not simply evaluate all \( n! \) permutations at once and automatically return the best one - an assumption that, unfortunately, is still common. Once you measure the output of a quantum algorithm, you effectively collapse the wavefunction, ending up with a single measured state. Thus, careful algorithm design is required to boost the probability of measuring the correct solution, often requiring many repeated measurements. A relevant quantum algorithm in this context is Grover’s Algorithm, which offers a quadratic speedup in unstructured searches (e.g., from \( O(2^n) \) to \( O(\sqrt{2^n}) \)). However, TSPs and other optimization problems have enough internal structure in practice that classical approaches can exploit it, often rendering Grover’s quadratic speedup unimpressive by comparison.
Quantum computers also come with significant drawbacks relative to classical computers. Their quantum state collapses upon measurement, preventing techniques like “early abort” or classical branch-and-bound pruning, where large portions of the search space can be discarded based on intermediate results. Classical algorithms rely on this kind of dynamic pruning to speed up the search. Quantum computing sacrifices flexibility for parallel evaluation—an advantage in unstructured or purely guesswork-based problems, but most practical optimization problems have exploitable structure. While there may be ways around these limitations and, in theory, quantum computers are more powerful than classical ones, whether this yields substantial real-world benefits for optimization remains unclear.
In some sense, quantum computers face challenges reminiscent of GPU computing: both process many data points in parallel (Single-Instruction, Multiple-Data), but lose out on some flexibility since every thread must follow identical instructions. Even for GPUs, applying them effectively to large-scale optimization has proven tricky, though progress continues.
If you want more perspectives on the topic, the following articles may be of interest:
- Challenges and Opportunities in Quantum Optimization: This preprint gives on 72 pages an extensive and well-written overview of the state of the art in quantum optimization. While the conclusion sounds quite optimistic, the paper is very clear about the current limitations and challenges. while it caters a scientific audience, it is still quite accessible.
- The travelling salesperson problem and the challenges of near-term quantum advantage: In this paper, Smith-Miles et al. argue why the TSP is unlikely to benefit from quantum computing in the foreseeable future. They also draw parallels to the failed attempts to solve the TSP with neural networks.
- Understanding instance hardness for optimisation algorithms: Methodologies, open challenges and post-quantum implications: This paper states that “it seems likely that there will be no quantum advantage for the TSP” due to challenges in tuning the parameters of QUBOs to even yield feasible solutions. However, it considers unconstrained optimization problems such as the MAX-CUT to have a higher chance of benefiting from quantum computing.
- Disentangling Hype from Practicality: On Realistically Achieving Quantum Advantage Gives strong arguments why it can be hard to achieve quantum advantage in practice, especially why quadratic speedup algorithms like Grover’s Algorithm will not suffice.
- Quantum advantage for NP approximation? For REAL this time?: A blog post by Scott Aaronson, a well-known quantum computing expert, offering a critical take on the QAOA algorithm and its claimed advantages.
- Challenges and opportunities in quantum optimization: A balanced discussion by a group of researchers, highlighting potential opportunities without making unfounded claims.
- Quantum Annealing versus Digital Computing: An Experimental Comparison: This paper compares quantum annealing to classical computing for optimization problems and found no indication of a quantum advantage.
 I do not claim to be an expert in quantum computing, so please interpret my remarks with appropriate caution. This book is an open-source project; therefore, if you have any corrections or suggestions to help improve the material for the community, feel free to open an issue or submit a pull request on GitHub. |
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Large Neighborhood Search
Using CP-SAT for Bigger Problems with Large Neighborhood Search

CP-SAT is great at solving small and medium-sized problems. But what if you have a really big problem on your hands? One option might be to use a special kind of algorithm known as a “meta-heuristic”, like a genetic algorithm. But these can be hard to set up and might not even give you good results.
Sometimes you will see new algorithms with cool-sounding names in scientific papers. While tempting, these are often just small twists on older methods and might leave out key details that make them work. If you are interested, there’s a discussion about this issue in a paper by Sörensen, called “Metaheuristics – The Metaphor Exposed”.
The good news? You do not have to implement an algorithm that simulates the mating behavior of forest frogs to solve your problem. If you already know how to use CP-SAT, you can stick with it to solve big problems without adding unnecessary complications. Even better? This technique, called Large Neighborhood Search, often outperforms all other approaches.
What Sets Large Neighborhood Search Apart?
Many traditional methods generate several “neighbor” options around an existing solution and pick the best one. However, making each neighbor solution takes time, limiting how many you can examine.
Large Neighborhood Search (LNS) offers a more efficient approach. Instead of generating neighbors one by one, LNS formulates a “mini-problem” that modifies parts of the current solution. This often involves randomly selecting some variables, resetting them, and using CP-SAT (or a similar tool) to find the optimal new values within the context of the remaining solution. This method, known as “destroy and repair,” allows for a broader exploration of neighbor solutions without constructing each one individually.
Moreover, LNS can easily be mixed with other methods like genetic algorithms. If you are already using a genetic algorithm, you could supercharge it by applying CP-SAT to find the best possible crossover of two or more existing solutions. It is like genetic engineering, but without any ethical worries!
When looking into the logs of CP-SAT, you may notice that it uses LNS itself to find better solutions.
8 incomplete subsolvers: [feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, rins/rens, rnd_cst_lns, rnd_var_lns]
Why does it not suffice to just run CP-SAT if it already solves the problem with LNS? The reason is that CP-SAT has to be relatively problem-agnostic. It has no way of knowing the structure of your problem and thus cannot use this information to improve the search. You on the other hand know a lot about your problem and can use this knowledge to implement a more efficient version.
Literature:
- General Paper on LNS-variants: Pisinger and Ropke - 2010
- A generic variant (RINS), that is also used by CP-SAT: Danna et al. 2005
We will now look into some examples to see this approach in action.
Example 1: Knapsack
You are given a knapsack that can carry a certain weight limit \( C \), and you have various items \( I \) you can put into it. Each item \( i\in I \) has a weight \( w_i \) and a value \( v_i \). The goal is to pick items to maximize the total value while staying within the weight limit.
\[ \max \sum_{i \in I} v_i x_i \]
\[ \text{s.t.} \sum_{i \in I} w_i x_i \leq C \]
\[ x_i \in \{0,1\} \]
This is one of the simplest NP-hard problems and can be solved with a dynamic programming approach in pseudo-polynomial time. CP-SAT is also able to solve many large instances of this problem in an instant. However, its simple structure makes it a good example to demonstrate the use of Large Neighborhood Search, even if the algorithm will not be of much use for this problem.
A simple idea for the LNS is to delete some elements from the current solution, compute the remaining capacity after deletion, select some additional items from the remaining items, and try to find the optimal solution to fill the remaining capacity with the deleted items and the newly selected items. Repeat this until you are happy with the solution quality. The number of items you delete and select can be fixed such that the problem can be easily solved by CP-SAT. You can find a full implementation under examples/lns_knapsack.ipynb.
Let us look only on an example here:
Instance: \( C=151 \), \( I=I_{0}(w=12, v=37),I_{1}(w=16, v=49),I_{2}(w=20, v=53),I_{3}(w=11, v=14),I_{4}(w=19, v=42), \) \( \quad I_{5}(w=13, v=53),I_{6}(w=18, v=54),I_{7}(w=16, v=56),I_{8}(w=14, v=45),I_{9}(w=12, v=39), \) \( \quad I_{10}(w=11, v=42),I_{11}(w=19, v=43),I_{12}(w=12, v=43),I_{13}(w=19, v=66),I_{14}(w=20, v=54), \) \( \quad I_{15}(w=13, v=54),I_{16}(w=12, v=33),I_{17}(w=12, v=38),I_{18}(w=14, v=43),I_{19}(w=15, v=28), \) \( \quad I_{20}(w=11, v=47),I_{21}(w=10, v=31),I_{22}(w=20, v=97),I_{23}(w=10, v=35),I_{24}(w=19, v=56), \) \( \quad I_{25}(w=11, v=33),I_{26}(w=12, v=38),I_{27}(w=15, v=45),I_{28}(w=17, v=58),I_{29}(w=11, v=48), \) \( \quad I_{30}(w=15, v=32),I_{31}(w=17, v=67),I_{32}(w=15, v=43),I_{33}(w=16, v=41),I_{34}(w=18, v=42), \) \( \quad I_{35}(w=14, v=44),I_{36}(w=20, v=45),I_{37}(w=13, v=50),I_{38}(w=17, v=57),I_{39}(w=17, v=33), \) \( \quad I_{40}(w=17, v=49),I_{41}(w=12, v=21),I_{42}(w=14, v=37),I_{43}(w=20, v=74),I_{44}(w=14, v=55), \) \( \quad I_{45}(w=10, v=25),I_{46}(w=16, v=26),I_{47}(w=10, v=37),I_{48}(w=18, v=63),I_{49}(w=16, v=39), \) \( \quad I_{50}(w=16, v=57),I_{51}(w=16, v=47),I_{52}(w=10, v=43),I_{53}(w=12, v=30),I_{54}(w=12, v=40), \) \( \quad I_{55}(w=19, v=48),I_{56}(w=12, v=39),I_{57}(w=14, v=43),I_{58}(w=17, v=35),I_{59}(w=19, v=51), \) \( \quad I_{60}(w=16, v=48),I_{61}(w=19, v=72),I_{62}(w=16, v=45),I_{63}(w=19, v=88),I_{64}(w=15, v=20), \) \( \quad I_{65}(w=17, v=49),I_{66}(w=14, v=40),I_{67}(w=14, v=27),I_{68}(w=19, v=51),I_{69}(w=10, v=37), \) \( \quad I_{70}(w=15, v=42),I_{71}(w=13, v=29),I_{72}(w=20, v=87),I_{73}(w=13, v=28),I_{74}(w=15, v=38), \) \( \quad I_{75}(w=19, v=77),I_{76}(w=13, v=35),I_{77}(w=17, v=55),I_{78}(w=13, v=39),I_{79}(w=10, v=26), \) \( \quad I_{80}(w=15, v=32),I_{81}(w=12, v=40),I_{82}(w=11, v=21),I_{83}(w=18, v=82),I_{84}(w=13, v=41), \) \( \quad I_{85}(w=12, v=27),I_{86}(w=15, v=35),I_{87}(w=18, v=48),I_{88}(w=15, v=64),I_{89}(w=19, v=62), \) \( \quad I_{90}(w=20, v=64),I_{91}(w=13, v=45),I_{92}(w=19, v=64),I_{93}(w=18, v=83),I_{94}(w=11, v=38), \) \( \quad I_{95}(w=10, v=30),I_{96}(w=18, v=65),I_{97}(w=19, v=56),I_{98}(w=12, v=41),I_{99}(w=17, v=36) \)
Initial solution of value 442: \( \{I_{0}, I_{1}, I_{2}, I_{3}, I_{4}, I_{5}, I_{6}, I_{7}, I_{8}, I_{9}\} \)
We will now repeatedly delete 5 items from the current solution and try to fill the newly gained capacity with an optimal solution built from the deleted items and 10 additional items. Note that this approach essentially considers \( 2^{5+10}=32768 \) neighbored solutions in each iteration. However, we could easily scale it up to consider \( 2^{100+900}\sim 10^{300} \) neighbored solutions in each iteration thanks to the implicit representation of the neighbored solutions and CP-SAT ability to prune large parts of the search space.
Round 1 of LNS algorithm:
- Deleting the following 5 items from the solution: \( \{I_{0}, I_{7}, I_{8}, I_{9}, I_{6}\} \)
- Repairing solution by considering the following subproblem:
- Subproblem: \( C=72 \), \( I=\{I_{6},I_{9},I_{86},I_{13},I_{47},I_{73},I_{0},I_{8},I_{7},I_{38},I_{57},I_{11},I_{60},I_{14}\} \)
- Computed the following solution of value 244 for the subproblem: \( \{I_{8}, I_{9}, I_{13}, I_{38}, I_{47}\} \)
- Combining \( \{I_{1}, I_{2}, I_{3}, I_{4}, I_{5}\}\cup \{I_{8}, I_{9}, I_{13}, I_{38}, I_{47}\} \)
- New solution of value 455: \( \{I_{1}, I_{2}, I_{3}, I_{4}, I_{5}, I_{8}, I_{9}, I_{13}, I_{38}, I_{47}\} \)
Round 2 of LNS algorithm:
- Deleting the following 5 items from the solution: \( \{I_{3}, I_{13}, I_{2}, I_{9}, I_{1}\} \)
- Repairing solution by considering the following subproblem:
- Subproblem: \( C=78 \), \( I=\{I_{13},I_{9},I_{84},I_{41},I_{15},I_{42},I_{74},I_{16},I_{3},I_{1},I_{2},I_{67},I_{50},I_{89},I_{43}\} \)
- Computed the following solution of value 275 for the subproblem: \( \{I_{1}, I_{15}, I_{43}, I_{50}, I_{84}\} \)
- Combining \( \{I_{4}, I_{5}, I_{8}, I_{38}, I_{47}\}\cup \{I_{1}, I_{15}, I_{43}, I_{50}, I_{84}\} \)
- New solution of value 509: \( \{I_{1}, I_{4}, I_{5}, I_{8}, I_{15}, I_{38}, I_{43}, I_{47}, I_{50}, I_{84}\} \)
Round 3 of LNS algorithm:
- Deleting the following 5 items from the solution: \( \{I_{8}, I_{43}, I_{84}, I_{1}, I_{50}\} \)
- Repairing solution by considering the following subproblem:
- Subproblem: \( C=79 \), \( I=\{I_{84},I_{76},I_{34},I_{16},I_{37},I_{20},I_{8},I_{43},I_{50},I_{1},I_{12},I_{35},I_{53}\} \)
- Computed the following solution of value 283 for the subproblem: \( \{I_{8}, I_{12}, I_{20}, I_{37}, I_{50}, I_{84}\} \)
- Combining \( \{I_{4}, I_{5}, I_{15}, I_{38}, I_{47}\}\cup \{I_{8}, I_{12}, I_{20}, I_{37}, I_{50}, I_{84}\} \)
- New solution of value 526: \( \{I_{4}, I_{5}, I_{8}, I_{12}, I_{15}, I_{20}, I_{37}, I_{38}, I_{47}, I_{50}, I_{84}\} \)
Round 4 of LNS algorithm:
- Deleting the following 5 items from the solution: \( \{I_{37}, I_{4}, I_{20}, I_{5}, I_{15}\} \)
- Repairing solution by considering the following subproblem:
- Subproblem: \( C=69 \), \( I=\{I_{37},I_{4},I_{20},I_{15},I_{82},I_{41},I_{56},I_{76},I_{85},I_{5},I_{32},I_{57},I_{7},I_{67}\} \)
- Computed the following solution of value 260 for the subproblem: \( \{I_{5}, I_{7}, I_{15}, I_{20}, I_{37}\} \)
- Combining \( \{I_{8}, I_{12}, I_{38}, I_{47}, I_{50}, I_{84}\}\cup \{I_{5}, I_{7}, I_{15}, I_{20}, I_{37}\} \)
- New solution of value 540: \( \{I_{5}, I_{7}, I_{8}, I_{12}, I_{15}, I_{20}, I_{37}, I_{38}, I_{47}, I_{50}, I_{84}\} \)
Round 5 of LNS algorithm:
- Deleting the following 5 items from the solution: \( \{I_{38}, I_{12}, I_{20}, I_{47}, I_{37}\} \)
- Repairing solution by considering the following subproblem:
- Subproblem: \( C=66 \), \( I=\{I_{20},I_{47},I_{37},I_{86},I_{58},I_{56},I_{54},I_{38},I_{12},I_{39},I_{68},I_{75},I_{66},I_{2},I_{99}\} \)
- Computed the following solution of value 254 for the subproblem: \( \{I_{12}, I_{20}, I_{37}, I_{47}, I_{75}\} \)
- Combining \( \{I_{5}, I_{7}, I_{8}, I_{15}, I_{50}, I_{84}\}\cup \{I_{12}, I_{20}, I_{37}, I_{47}, I_{75}\} \)
- New solution of value 560: \( \{I_{5}, I_{7}, I_{8}, I_{12}, I_{15}, I_{20}, I_{37}, I_{47}, I_{50}, I_{75}, I_{84}\} \)
Example 2: Different Neighborhoods for the Traveling Salesman Problem
Simply removing a portion of the solution and then trying to fix it is not the most effective approach. In this section, we will explore various neighborhoods for the Traveling Salesman Problem (TSP). The geometry of TSP not only permits advantageous neighborhoods but also offers visually appealing representations. When you have several neighborhood strategies, they can be dynamically integrated using an Adaptive Large Neighborhood Search (ALNS).
The image illustrates an optimization process for a tour that needs to traverse the green areas, factoring in turn costs, within an embedded graph (mesh). The optimization involves choosing specific regions (highlighted in red) and calculating the optimal tour within them. As iterations progress, the initial tour generally improves, although some iterations may not yield any enhancement. Regions in red are selected due to the high cost of the tour within them. Once optimized, the center of that region is added to a tabu list, preventing it from being chosen again.
 |
|---|
| Large Neighbordhood Search for Coverage Path Planning by repeatedly selecting a geometric region (red) and optimizing the tour within it. The red parts of the tour highlight the changes in the iteration. Read from left to right, and from up to down. |
How can you determine the appropriate size of a region to select? You have two main options: conduct preliminary experiments or adjust the size adaptively during the search. Simply allocate a time limit for each iteration. If the solver does not optimize within that timeframe, decrease the region size. Conversely, if it does, increase the size. Utilizing exponential factors will help the size swiftly converge to its optimal dimension. However, it’s essential to note that this method assumes subproblems are of comparable difficulty and may necessitate additional conditions.
For the Euclidean TSP, as opposed to a mesh, optimizing regions is not straightforward. Multiple effective strategies exist, such as employing a segment from the previous tour rather than a geometric region. By implementing various neighborhoods and evaluating their success rates, you can allocate a higher selection probability to the top-performing ones. This approach is demonstrated in an animation crafted by two of my students, Gabriel Gehrke and Laurenz Illner. They incorporated four distinct neighborhoods and utilized ALNS to dynamically select the most effective one.
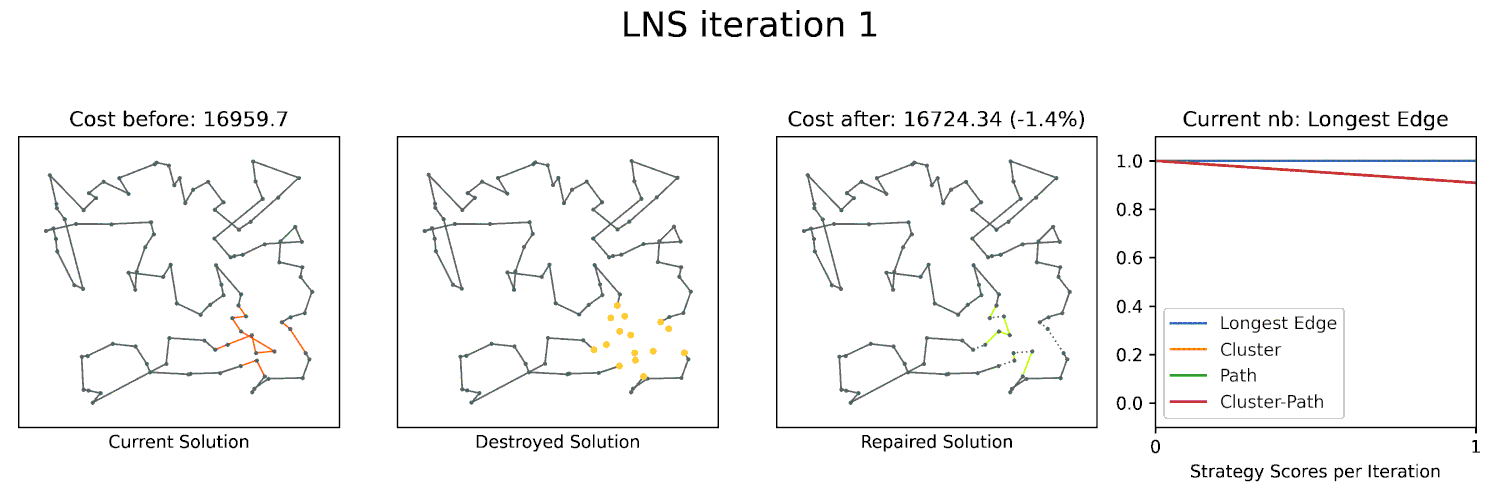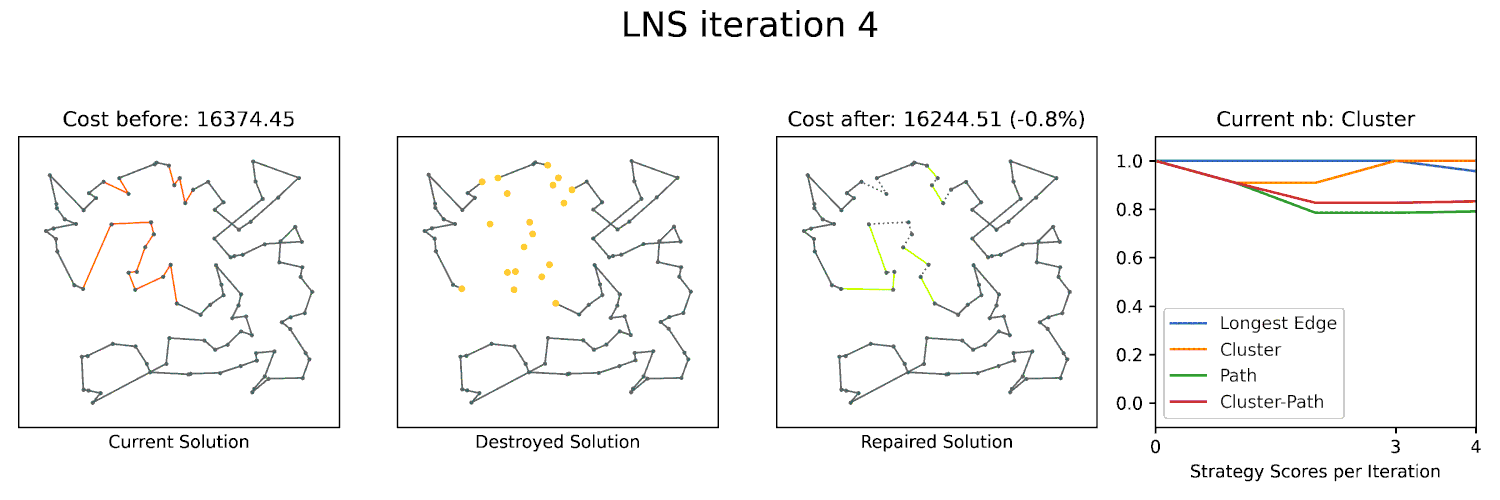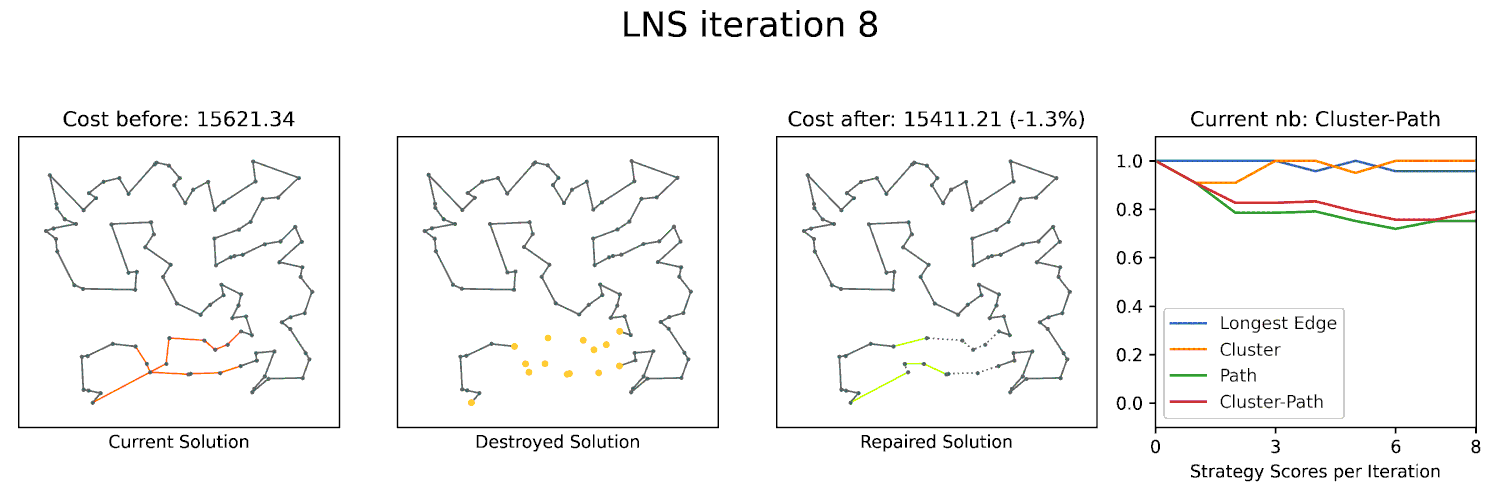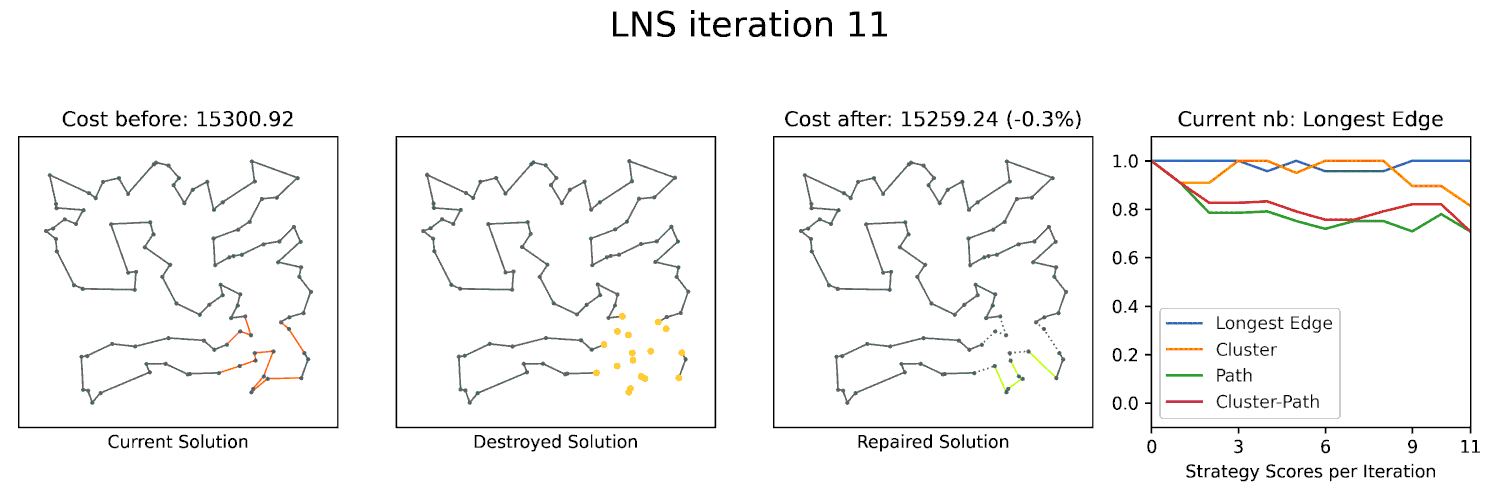 |
|---|
| Animation of an Adaptive Large Neighborhood Search for the classical Traveling Salesman Problem. It uses four different neighborhood strategies which are selected randomly with a probability based on their success rate in previous iterations. If you check the logs of the latest (v9.8) version of CP-SAT, it also rates the performance of its LNS-strategies and uses the best performing strategies more often (UCB1-algorithm). |
Multi-Armed Bandit: Exploration vs. Exploitation
Having multiple strategies for each iteration of your Large Neighborhood Search (LNS) is beneficial, but how do you decide which one to use? While you could select a strategy at random, this approach is inefficient because it is unlikely to choose the best one. Alternatively, you could stick to the strategy that performed well in the past, but there may be a better option you have not tried yet. This brings us to the classic exploration vs. exploitation dilemma. On one hand, you want to exploit strategies that have proven successful, but on the other, you need to explore new strategies to discover potentially better ones.
Fortunately, this issue has been widely studied as the Multi-Armed Bandit Problem, and there are numerous effective solutions available. One popular approach is the Upper Confidence Bound (UCB1) algorithm. I wanted to highlight this dilemma to make you aware that many experts have already tackled it and developed sophisticated strategies.
In practice, CP-SAT schedules its LNS strategies using a simple round-robin
method, as reflected by their equal number of calls in the logs. Whenever a
worker thread finishes its work, it will execute an iteration with the next
strategy in the list, leading to a fair distribution of calls. In this case, we
can see that the 'routing_path_lns' strategy was the most successful,
improving the incumbent solution 41 times out of 65 calls. There might be room
for performance improvements by employing a more advanced strategy selection
algorithm. However, it is important to recognize the relatively low number of
calls to each strategy in combination with diminishing and noisy returns. If you
only have a few iterations, a more advanced algorithm may not have enough data
to make reliable decisions.
LNS stats Improv/Calls Closed Difficulty TimeLimit
'graph_arc_lns': 5/65 49% 0.26 0.10
'graph_cst_lns': 4/65 54% 0.47 0.10
'graph_dec_lns': 3/65 49% 0.26 0.10
'graph_var_lns': 4/66 55% 0.56 0.10
'rins/rens': 23/66 39% 0.03 0.10
'rnd_cst_lns': 12/66 50% 0.19 0.10
'rnd_var_lns': 6/66 52% 0.36 0.10
'routing_path_lns': 41/65 48% 0.10 0.10
'routing_random_lns': 24/65 52% 0.26 0.10
 We have found the following simple procedure effective:
|
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.
Benchmarking your Model
Benchmarking your Model

This chapter explores methods for comparing the performance of different models applied to complex problems, where the basic model leaves room for improvement — either in runtime or in solution quality, especially when the model cannot always be solved to optimality. As a scientist writing a paper on a new model (or, more likely, a new algorithm that internally uses a model), this will be the default case as research on a problem that can already be solved well is hard to publish. Whether you aim merely to evaluate whether your new approach outperforms the current one or intend to prepare a formal scientific publication, you face the same challenges; in the latter case, however, the process becomes more extensive and formalized (but this may also be true for the first case depending on your manager).
 In some cases, the primary performance bottleneck may not lie within CP-SAT
itself but rather in the Python code used to generate the model.
Identifying the most resource-intensive segments of your Python code is
therefore essential. The profiler
Scalene has proven to be
particularly effective for pinpointing such issues. In many situations, simple
logging statements (e.g.,
|
During the explorative phase, when you probe different ideas, you will likely select one to five instances that you can run quickly and compare. However, for most applications, this number is insufficient, and you risk overfitting your model to these instances — gaining performance improvements on them but sacrificing performance on others. You may even limit your model’s ability to solve certain instances.
A classic example involves deactivating specific CP-SAT search strategies or preprocessing steps that have not yielded benefits on the selected instances. If your instance set is large enough, the risk is low; however, if you have only a few instances, you may remove the single strategy necessary to solve a particular class of problems. Modern solvers include features that impose a modest overhead on simple instances but enable solving otherwise intractable cases. This trade-off is worthwhile: do not sacrifice the ability to solve complex instances for a marginal performance gain on simple ones. Therefore, always benchmark your changes properly before deploying them to production, even if you do not plan to publish your results scientifically.
Note that this chapter focuses solely on improving the performance of your model with respect to its specific formulation; it does not address the evaluation of the model’s accuracy or its business value. When tackling a real-world problem, where your model is merely an approximation of reality, it is essential to also consider refining the approximation and monitoring the real-world performance of the resulting solutions. In some cases, simpler formulations not only yield better outcomes but are also easier to optimize for.
No-Free-Lunch Theorem and Timeouts
The no‐free‐lunch theorem and timeouts complicate benchmarking more than you might have anticipated. The no‐free‐lunch theorem asserts that no single algorithm outperforms all others across every instance, which is especially true for NP‐hard problems. Consequently, improving performance on some instances often coincides with degradations on others. It is essential to assess whether the gains justify the losses.
Another challenge arises when imposing a time limit to prevent individual instances from running indefinitely. Without such a limit, benchmark runs can become prohibitively long. However, including aborted runs in the dataset complicates performance evaluation, as it remains unclear whether a solver would have found a solution shortly after the timeout or was trapped in an infinite loop. Discarding all instances that timed out on a particular model restricts the evaluation to simpler instances, even though the more complex ones are often of greater interest. Conversely, discarding all models that timed out on any instance may leave no viable candidates, as any solver is likely to fail on at least one instance in a sufficiently large benchmark set. Whether the goal is to find a provably optimal solution, the best solution within a fixed time limit, or simply any feasible solution, it is essential to enable comparisons over data sets that include unknown outcomes.
Example: Nurse Rostering Problem Benchmark
Let us examine the performance of CP-SAT, Gurobi, and Hexaly on a Nurse Rostering Problem to illustrate the additional challenge of selecting an appropriate time limit. Nurse rostering is a complex yet common problem in which nurses must be assigned to shifts while satisfying a variety of constraints. Since CP-SAT, Gurobi, and Hexaly differ significantly in their underlying algorithms, the comparison reveals pronounced performance differences. However, such patterns can also be observed when using the same solver across instances, albeit usually not as pronounced.
The following two plots illustrate the value of the incumbent solution (i.e., the best solution found so far) and the best proven lower bound during the search. These are challenging instances, and only Gurobi is able to find an optimal solution.
Notably, the best-performing solver changes depending on the allotted computation time. For this problem, Hexaly excels at finding good initial solutions quickly but tends to stall thereafter. CP-SAT requires slightly more time to get started but demonstrates steady progress. In contrast, Gurobi begins slowly but eventually makes substantial improvements.
So, which solver is best for this problem?
 |
|---|
| Performance comparison of CP-SAT, Gurobi, and Hexaly on instance 19 of the Nurse Rostering Problem Benchmark. Hexaly starts strong but is eventually overtaken by CP-SAT. Gurobi surpasses Hexaly near the end by a small margin. CP-SAT and Gurobi converge to nearly the same lower bound. |
 |
|---|
| Performance comparison of CP-SAT, Gurobi, and Hexaly on instance 20 of the Nurse Rostering Problem Benchmark. Hexaly again performs well early but is outperformed by CP-SAT. Gurobi maintains a poor incumbent value for most of the runtime but eventually makes a significant improvement and proves optimality. The optimal solution is visibly superior to CP-SAT’s best solution. CP-SAT is unable to prove a meaningful lower bound for this instance. |
 These two plots (and even this specific problem) are insufficient to draw definitive conclusions about the overall performance of the solvers. Nevertheless, it is remarkable that our beloved open-source solver, CP-SAT, performs so well against the commercial solvers Gurobi and Hexaly in this context. |
If provably optimal solutions are required, Gurobi may be the most suitable choice; however, the likelihood of achieving optimality is low for most instances. If your instances are expected to grow in size and require fast solutions, Hexaly might be preferable, as it appears highly effective at finding good solutions quickly. This observation is also supported by preliminary results on larger instances, for which neither CP-SAT nor Gurobi find any feasible solution. CP-SAT, by contrast, offers a strong compromise between the two: although it starts more slowly, it maintains consistent progress throughout the search.
 A commonly used metric for convergence is the primal integral, which measures the area under the curve of the incumbent solution value over time. It provides a single scalar that summarizes how quickly a solver improves its best-known solution. CP-SAT reports a related metric: the integral of the logarithm of the optimality gap, which also accounts for the quality of the bound. These metrics offer an objective measure of solver progress over time, though they may not fully capture problem-specific or subjective priorities. |
Defining Your Benchmarking Goals
The first step is to determine your specific requirements and how best to measure solver performance accordingly. It is not feasible to manually plot performance for every instance and assign scores based on subjective impressions; such an approach does not scale and lacks objectivity and reproducibility. Instead, you should define a concrete metric that accurately reflects your goals. One strategy is to carefully select benchmark instances that are still likely to be solved to optimality, with the expectation that performance trends will generalize to larger instances. Another to decide for a fixed time limit we are willing to wait for a solution, and then measure how well each solver performs under these constraints. While no evaluation method will be perfect, it is essential to remain aware of potential threats to the validity of your results. Let us go through some common scenarios.
 Empirical studies on algorithms have historically faced some tension within the academic community, where theoretical results are often viewed as more prestigious or fundamental. The paper Needed: An Empirical Science of Algorithms by John Hooker (1994) offers a valuable historical and philosophical perspective on this issue. |
Common Benchmarking Scenarios and Visualization Techniques
Several common benchmarking scenarios arise in practice. To select an appropriate visualization or evaluation method, it is important to first identify which scenario applies to your case and to recognize which tools are better suited for other contexts. Avoid choosing the most visually appealing or complex plot by default; instead, select the one that best serves your analytical goals. Keep in mind that the primary purpose of a plot is to make tabular data more accessible and easier to interpret. It does not replace the underlying tables, nor does it provide definitive answers.
-
Instances are always solved to optimality, and only runtime matters. This is the simplest benchmarking scenario. If every instance can be solved to optimality and your only concern is runtime, you can summarize performance using the mean (relative) runtime or visualize it using a basic box plot. The primary challenge here lies in choosing the appropriate type of mean (e.g., arithmetic, geometric, harmonic) and selecting representative instances that reflect production-like conditions. For this case, the rest of the chapter may be skipped.
-
Optimal or feasible solutions are sought, but may not always be found within the time limit. When timeouts occur, runtimes for unsolved instances become unknown, making traditional means unreliable. In such cases, cactus plots are an effective way to visualize solver performance, even in the presence of incomplete data.
-
The goal is to find the best possible solution within a fixed time limit. Here, the focus is on solution quality under time constraints, rather than on whether optimality is reached. Performance plots are especially suitable for this purpose, as they reveal how closely each solver or model approaches the best-known solution across the benchmark set.
-
Scalability analysis: how performance evolves with instance size. If you are analyzing how well a model scales, i.e., how large an instance it can solve to optimality and how the optimality gap grows thereafter, split plots are a good choice. They show runtime for solved instances and optimality gap for those that exceed the time limit, allowing for a unified view of scalability.
-
Multi-metric performance comparison against a baseline. When you want a quick, intuitive overview of how your model performs across several metrics, such as runtime, objective value, and lower bound, scatter plots with performance zones are ideal. They provide a clear comparative visualization, making it easy to spot outliers and trade-offs across dimensions.
 Use the SIGPLAN Empirical Evaluation Checklist if your evaluation has to satisfy academic standards. |
Quickly Comparing to a Baseline Using Scatter Plots
Scatter plots with performance zones are, in my experience, highly effective for
quickly comparing the performance of a prototype against a baseline across
multiple metrics. While these plots do not provide a formal quantitative
evaluation, they offer a clear visual overview of how performance has shifted.
Their key advantages are their intuitive readability and their ability to
accommodate NaN values. They are particularly useful for identifying outliers,
though they can be less effective when too many points overlap or when data
ranges vary significantly (sometimes, a log scale can help here).
Consider the following example table, which compares a basic optimization model
with a prototype model in terms of runtime, objective value, and lower bound.
The runtime is capped at 90 seconds, and if no optimal solution is found within
this limit, the objective value is set to NaN. A run only terminates before
the time limit if an optimal solution is found.
Example Data
| instance_name | strategy | runtime | objective | lower_bound |
|---|---|---|---|---|
| att48 | Prototype | 89.8327 | 33522 | 33522 |
| att48 | Baseline | 90.1308 | 33522 | 33369 |
| eil101 | Prototype | 90.0948 | 629 | 629 |
| eil101 | Baseline | 43.8567 | 629 | 629 |
| eil51 | Prototype | 84.8225 | 426 | 426 |
| eil51 | Baseline | 3.05334 | 426 | 426 |
| eil76 | Prototype | 90.2696 | 538 | 538 |
| eil76 | Baseline | 4.09839 | 538 | 538 |
| gil262 | Prototype | 90.3314 | 13817 | 2368 |
| gil262 | Baseline | 90.8782 | 3141 | 2240 |
| kroA100 | Prototype | 90.5127 | 21282 | 21282 |
| kroA100 | Baseline | 90.0241 | 22037 | 20269 |
| kroA150 | Prototype | 90.531 | 27249 | 26420 |
| kroA150 | Baseline | 90.3025 | 27777 | 24958 |
| kroA200 | Prototype | 90.0019 | 176678 | 29205 |
| kroA200 | Baseline | 90.7658 | 32749 | 27467 |
| kroB100 | Prototype | 90.1334 | 22141 | 22141 |
| kroB100 | Baseline | 90.5845 | 22729 | 21520 |
| kroB150 | Prototype | 90.7107 | 128751 | 26016 |
| kroB150 | Baseline | 90.9659 | 26891 | 25142 |
| kroB200 | Prototype | 90.7931 | 183078 | 29334 |
| kroB200 | Baseline | 90.3594 | 34481 | 27708 |
| kroC100 | Prototype | 90.5131 | 20749 | 20749 |
| kroC100 | Baseline | 90.3035 | 21118 | 20125 |
| kroD100 | Prototype | 90.0728 | 21294 | 21294 |
| kroD100 | Baseline | 90.2563 | 21294 | 20267 |
| kroE100 | Prototype | 90.4515 | 22068 | 22053 |
| kroE100 | Baseline | 90.6112 | 22341 | 21626 |
| lin105 | Prototype | 90.4714 | 14379 | 14379 |
| lin105 | Baseline | 90.6532 | 14379 | 13955 |
| lin318 | Prototype | 90.8489 | 282458 | 41384 |
| lin318 | Baseline | 90.5955 | 103190 | 39016 |
| linhp318 | Prototype | 90.9566 | nan | 41412 |
| linhp318 | Baseline | 90.7038 | 84918 | 39016 |
| pr107 | Prototype | 90.3708 | 44303 | 44303 |
| pr107 | Baseline | 90.4465 | 45114 | 27784 |
| pr124 | Prototype | 90.1689 | 59167 | 58879 |
| pr124 | Baseline | 90.8673 | 60760 | 52392 |
| pr136 | Prototype | 90.0296 | 96781 | 96772 |
| pr136 | Baseline | 90.2636 | 98850 | 89369 |
| pr144 | Prototype | 90.3141 | 58537 | 58492 |
| pr144 | Baseline | 90.6465 | 59167 | 33809 |
| pr152 | Prototype | 90.4742 | 73682 | 73682 |
| pr152 | Baseline | 90.8629 | 79325 | 46604 |
| pr226 | Prototype | 90.1845 | 1.19724e+06 | 74474 |
| pr226 | Baseline | 90.6676 | 103271 | 55998 |
| pr264 | Prototype | 90.4012 | 736226 | 41020 |
| pr264 | Baseline | 90.9642 | 68802 | 37175 |
| pr299 | Prototype | 90.3325 | nan | 47375 |
| pr299 | Baseline | 90.19 | 120489 | 45594 |
| pr439 | Prototype | 90.5761 | nan | 95411 |
| pr439 | Baseline | 90.459 | 834126 | 93868 |
| pr76 | Prototype | 90.2718 | 108159 | 107727 |
| pr76 | Baseline | 90.2951 | 110331 | 105340 |
| st70 | Prototype | 90.2824 | 675 | 675 |
| st70 | Baseline | 90.1484 | 675 | 663 |
From the table, we can already spot some fundamental issues. For example, the prototype fails on three instances, and several instances yield significantly worse results than the baseline. However, when we turn to the scatter plots with performance zones, such anomalies become immediately apparent.
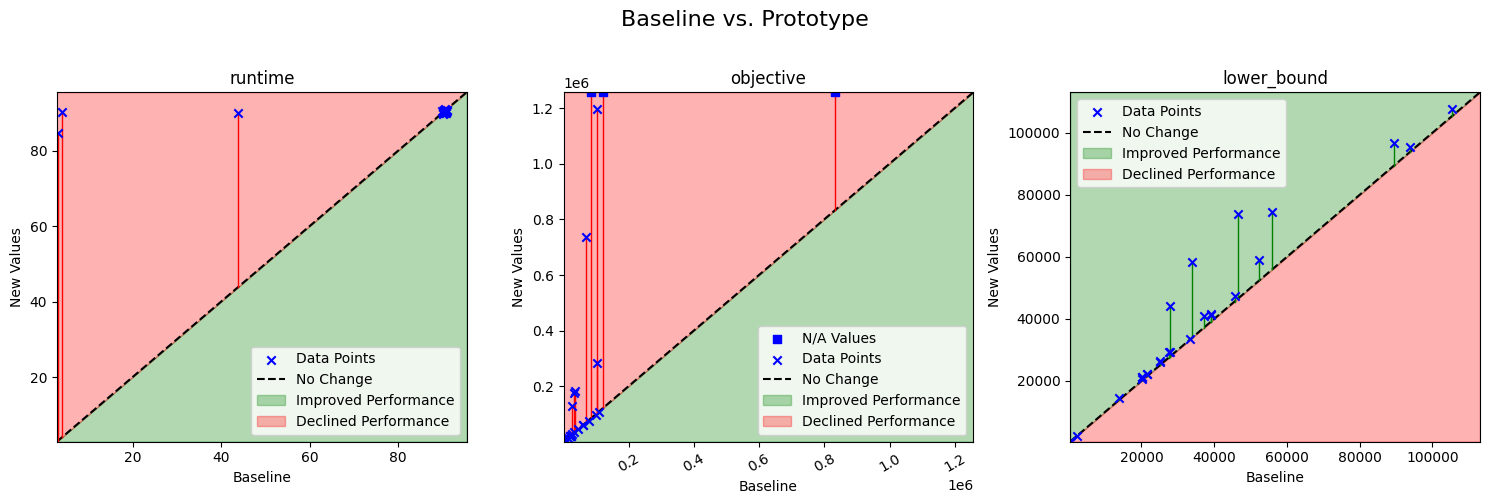 |
|---|
| Scatter plot comparing the performance of a prototype model against a baseline model across three metrics: runtime, objective value, and lower bound. The x-axis represents the baseline model’s performance; the y-axis shows the prototype model’s performance. Color-coded zones indicate relative performance levels, making it easier to identify where the prototype outperforms or underperforms the baseline. |
For runtime, both models typically hit the time limit, so there is limited variation to observe. However, the baseline model solves a few instances significantly faster, whereas the prototype consistently uses the full time limit. For the objective value, both models produce similar results on most instances. Yet, particularly on the larger instances, the prototype yields either very poor or no solutions at all.
Interestingly, the lower bounds produced by the prototype are much better for some instances. This improvement was not obvious from a cursory review of the table but becomes immediately noticeable in the plots.
Scatter plots are also highly effective when working with multiple performance metrics, particularly when you want to ensure that gains in one metric do not come at the expense of unacceptable losses in another. In practice, it is often difficult to precisely quantify the relative importance of each metric from the outset. The intuitive nature of these plots offers a valuable overview, serving as a visual aid before you commit to a specific performance metric. The example below illustrates a hypothetical scenario involving a vehicle routing problem.
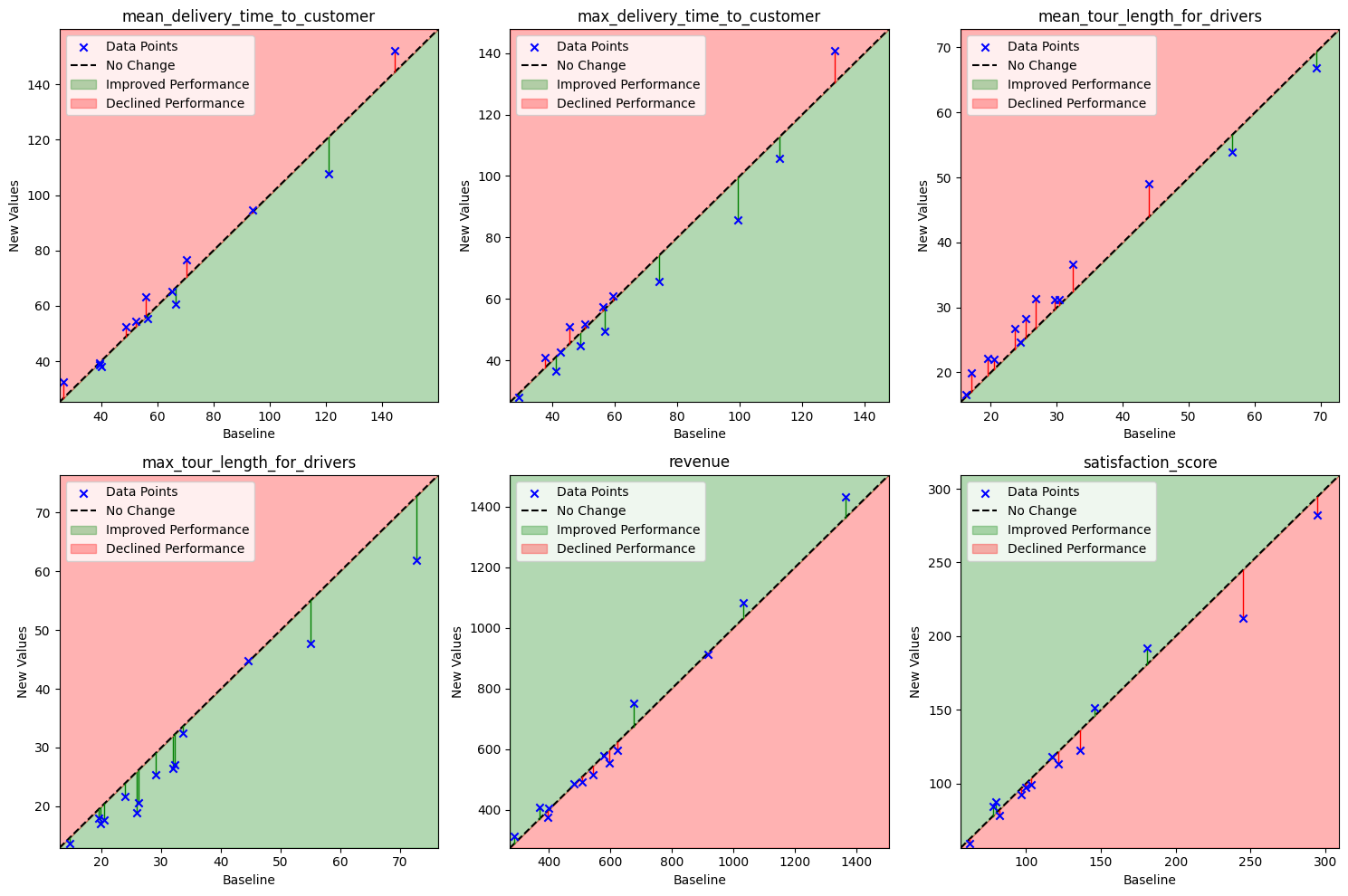 |
|---|
| Scatter plots illustrating performance trade-offs across multiple metrics in a hypothetical vehicle routing problem. These plots help assess whether improvements in one metric come at the cost of significant regressions in another. Their intuitive layout makes them especially useful when metric priorities are not yet clearly defined, offering a quick overview of relative performance and highlighting outliers across different algorithm versions. |
Here is the code I used to generate the plots. You can freely copy and use it.
"""
This module contains functions to plot a scatter comparison of baseline and new values with performance areas highlighted.
You can freely use and distribute this code under the MIT license.
Changelog:
2024-08-27: First version
2024-08-29: Added lines to the diagonal to help with reading the plot
2025-06-07: Basic improvements and fixing issue with index comparison.
(c) 2025 Dominik Krupke, https://github.com/d-krupke/cpsat-primer
"""
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def plot_performance_scatter(
ax,
baseline: pd.Series,
new_values: pd.Series,
lower_is_better: bool = True,
title: str = "",
**kwargs,
):
"""
Plot a scatter comparison of baseline and new values with performance areas highlighted.
Parameters:
ax (matplotlib.axes.Axes): The axes on which to plot.
baseline (pd.Series): Series of baseline values.
new_values (pd.Series): Series of new values.
lower_is_better (bool): If True, lower values indicate better performance.
title (str): Title of the plot.
**kwargs: Additional keyword arguments for customization (e.g., 'color', 'marker').
"""
if not isinstance(baseline, pd.Series) or not isinstance(new_values, pd.Series):
raise ValueError("Both baseline and new_values should be pandas Series.")
if baseline.size != new_values.size:
raise ValueError("Both Series should have the same length.")
scatter_kwargs = {
"color": kwargs.get("color", "blue"),
"marker": kwargs.get("marker", "x"),
"label": kwargs.get("label", "Data Points"),
}
line_kwargs = {
"color": kwargs.get("line_color", "k"),
"linestyle": kwargs.get("line_style", "--"),
"label": kwargs.get("line_label", "No Change"),
}
fill_improve_kwargs = {
"color": kwargs.get("improve_color", "green"),
"alpha": kwargs.get("improve_alpha", 0.3),
"label": kwargs.get("improve_label", "Improved Performance"),
}
fill_decline_kwargs = {
"color": kwargs.get("decline_color", "red"),
"alpha": kwargs.get("decline_alpha", 0.3),
"label": kwargs.get("decline_label", "Declined Performance"),
}
# Replace inf values with NaN
baseline = baseline.replace([np.inf, -np.inf], np.nan)
new_values = new_values.replace([np.inf, -np.inf], np.nan)
max_val = max(baseline.max(skipna=True), new_values.max(skipna=True)) * 1.05
min_val = min(baseline.min(skipna=True), new_values.min(skipna=True)) * 0.95
# get indices of NA values
na_indices = baseline.isna() | new_values.isna()
if lower_is_better:
# replace NA values with max_val
baseline = baseline.fillna(max_val)
new_values = new_values.fillna(max_val)
else:
# replace NA values with min_val
baseline = baseline.fillna(min_val)
new_values = new_values.fillna(min_val)
# plot the na_indices with a different marker
if na_indices.any():
ax.scatter(
baseline[na_indices],
new_values[na_indices],
marker="s",
color=scatter_kwargs["color"],
label="N/A Values",
zorder=2,
)
# add the rest of the data points
ax.scatter(
baseline[~na_indices], new_values[~na_indices], **scatter_kwargs, zorder=2
)
ax.plot([min_val, max_val], [min_val, max_val], zorder=1, **line_kwargs)
x = np.linspace(min_val, max_val, 500)
if lower_is_better:
ax.fill_between(x, min_val, x, zorder=0, **fill_improve_kwargs)
ax.fill_between(x, x, max_val, zorder=0, **fill_decline_kwargs)
else:
ax.fill_between(x, x, max_val, zorder=0, **fill_improve_kwargs)
ax.fill_between(x, min_val, x, zorder=0, **fill_decline_kwargs)
# draw thin lines to the diagonal to help with reading the plot.
# A problem without lines is that one tends to use the distance
# to the diagonal as a measure of performance, which is not correct.
# Instead, it is `y-x` that should be used.
for old_val, new_val in zip(baseline, new_values):
if pd.isna(old_val) and pd.isna(new_val):
continue
if pd.isna(old_val):
old_val = min_val if lower_is_better else max_val
if pd.isna(new_val):
new_val = min_val if lower_is_better else max_val
if lower_is_better and new_val < old_val:
ax.plot(
[old_val, old_val],
[old_val, new_val],
color="green",
linewidth=1.0,
zorder=1,
)
elif not lower_is_better and new_val > old_val:
ax.plot(
[old_val, old_val],
[old_val, new_val],
color="green",
linewidth=1.0,
zorder=1,
)
elif lower_is_better and new_val > old_val:
ax.plot(
[old_val, old_val],
[old_val, new_val],
color="red",
linewidth=1.0,
zorder=1,
)
elif not lower_is_better and new_val < old_val:
ax.plot(
[old_val, old_val],
[old_val, new_val],
color="red",
linewidth=1.0,
zorder=1,
)
ax.set_xlim(min_val, max_val)
ax.set_ylim(min_val, max_val)
ax.set_xlabel(kwargs.get("xlabel", "Baseline"))
ax.set_ylabel(kwargs.get("ylabel", "New Values"))
if title:
ax.set_title(title)
ax.legend()
def plot_comparison_grid(
baseline_data: pd.DataFrame,
new_data: pd.DataFrame,
metrics: list[tuple[str, str]],
n_cols: int = 4,
figsize: tuple[int, int] | None = None,
suptitle: str = "",
subplot_kwargs: dict | None = None,
**kwargs,
):
"""
Plot a grid of performance comparisons for multiple metrics.
Parameters:
baseline_data (pd.DataFrame): DataFrame containing the baseline data.
new_data (pd.DataFrame): DataFrame containing the new data.
metrics (list of tuple of str): List of tuples containing column names and comparison direction ('min' or 'max').
n_cols (int): Number of columns in the grid.
figsize (tuple of int): Figure size (width, height).
suptitle (str): Title for the entire figure.
**kwargs: Additional keyword arguments to pass to individual plot functions.
Returns:
fig (matplotlib.figure.Figure): The figure object containing the plots.
axes (np.ndarray): Array of axes objects corresponding to the subplots.
"""
n_metrics = len(metrics)
n_cols = min(n_cols, n_metrics)
n_rows = (n_metrics + n_cols - 1) // n_cols # Ceiling division
# Validate columns and directions
for column, direction in metrics:
if direction not in {"min", "max"}:
raise ValueError("The direction should be either 'min' or 'max'.")
if column not in baseline_data.columns or column not in new_data.columns:
raise ValueError(f"Column '{column}' not found in the data.")
# Validate index alignment
if set(baseline_data.index) != set(new_data.index):
raise ValueError("Indices of the DataFrames do not match (different values).")
if figsize is None:
figsize = (5 * n_cols, 5 * n_rows)
fig, axes = plt.subplots(n_rows, n_cols, figsize=figsize)
axes = axes.flatten()
for ax, (column_name, direction) in zip(axes, metrics):
# Merge kwargs and subplot_kwargs[column_name] (if present) into a new dict
merged_kwargs = dict(kwargs)
if subplot_kwargs and column_name in subplot_kwargs:
merged_kwargs.update(subplot_kwargs[column_name])
plot_performance_scatter(
ax,
baseline_data[column_name],
new_data[column_name],
lower_is_better=(direction == "min"),
title=column_name,
**merged_kwargs,
)
# Turn off any unused subplots
for ax in axes[n_metrics:]:
ax.axis("off")
if suptitle:
fig.suptitle(suptitle, fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.96])
return fig, axes
Success-Based Benchmarking: Cactus Plots and PAR Metrics
The SAT community frequently uses cactus plots (also known as survival plots) to effectively compare the time to success of different solvers on a benchmark set, even when timeouts occur. If you are dealing with a pure constraint satisfaction problem, this approach is directly applicable. However, it can also be extended to other binary success indicators — such as proving optimality, even under optimality tolerances.
Additionally, the PAR10 metric is commonly used to summarize solver performance on a benchmark set. It is defined as the average time a solver takes to solve an instance, where unsolved instances (within the time limit) are penalized by assigning them a runtime equal to 10 times the cutoff. Variants like PAR2, which use a penalty factor of 2 instead of 10, are also encountered. While a factor of 10 is conventional, it remains an arbitrary choice. Ultimately, you must decide how to handle unknowns (instances not solved within the time limit) since you only know that their actual runtime exceeds the cutoff. If an explicit performance metric is required to declare a winner, PAR-style metrics are widely accepted but come with notable limitations.
To gain a more nuanced view of solver performance, cactus plots are often employed. In these plots, each solver is represented by a line where each point \( (x, y) \) indicates that \( y \) benchmark instances were solved within \( x \) seconds (there exists also the reversed version).
 |
|---|
| Each point \( (x, y) \) shows that \( x \) instances were solved within \( y \) seconds. |
The mean PAR10 scores for the four strategies in the example above are as follows:
| Strategy | PAR10 |
|---|---|
| AddCircuit | 512.133506 |
| Dantzig (Gurobi) | 66.452202 |
| Iterative Dantzig | 752.412118 |
| Miller-Tucker-Zemlin | 1150.014846 |
In case you are wondering, this is some data on solving the Traveling Salesman Problem (TSP) with different strategies. Gurobi dominates, but it is well-known that Gurobi is excellent at solving TSP.
If the number of solvers or models under comparison is not too large, you can also use a variation of the cactus plot to show solver performance under different optimality tolerances. This allows you to examine how much performance improves when the tolerance is relaxed. However, if your primary interest lies in solution quality, performance plots are likely to be more appropriate.
In the following example, different optimality tolerances reveal a visible
performance improvement for the strategies AddCircuit and
Miller-Tucker-Zemlin. For the other two strategies, the impact of tolerance
changes is minimal. This variation of the cactus plot can also be applied to
compare solver performance across different benchmark sets, especially if you
suspect significant variation across instance categories.
 |
|---|
| Each line style represents an optimality tolerance. The plot shows how many instances (\( y \)) can be solved within a given time limit (\( x \)) for each tolerance. |
It is also common practice to include a virtual best line in the cactus plot. This line indicates, for each instance, the best time achieved by any solver. Although it does not represent an actual solver, it serves as a valuable reference to evaluate the potential for solver complementarity. If one solver clearly dominates, the virtual best line will coincide with its curve. However, if the lines diverge, it suggests that no single solver is universally superior—a case of the “no free lunch” principle. Even if one solver performs best on 90% of instances, the remaining 10% may be better handled by alternatives. The greater the gap between the best actual solver and the virtual best, the stronger the case for a portfolio approach.
 A more detailed discussion on this type of plot can be found in the referenced academic paper: Benchmarking Solvers, SAT-style by Brain, Davenport, and Griggio |
Performance Plots for Solution Quality within a Time Limit
When dealing with instances that typically cannot be solved to optimality, performance plots are often more appropriate than cactus plots. These plots illustrate the relative performance of different models or solvers on a set of instances, usually under a fixed time limit. At the leftmost point of the plot (where \( x = 1 \)), each solver’s line indicates the proportion of instances for which it achieved the best-known solution (not necessarily exclusively). Then its \( (x,y) \) coordinates indicate the proportion \( y \) of instances for which the solver achieved a solution that is at most \( x \) times worse than the best known solution. For example, if a solver has a point at \( (1.05, 0.8) \), it means that it found a solution within 5% of the best-known solution for 80% of the instances. Often, a logarithmic scale is used for the x-axis, especially when the performance ratios vary widely. However, down below we use a linear scale because the values are close to 1.
In the example below, based on the Capacitated Vehicle Routing Problem (CVRP), the performance plots compare three different models across a benchmark set. These plots offer a clear visual summary of how closely each model approaches the best solution.
 |
|---|
Performance plot comparing the objective values of different CVRP models on a benchmark set. The Miller–Tucker–Zemlin model performs best on most instances and remains close to the best on the rest. The other two models find the best solution in only about 10% of instances but solve roughly 70% within 2% of the best known solution, with multiple_circuit showing a slight advantage. |
This can of course also be done for the lower bounds produced by each model.
 |
|---|
Performance plot comparing the lower bounds produced by each CVRP model. The add_circuit model consistently achieves the best bounds, while the other two models yield bounds that are up to 20% worse in the best case and up to 100% worse (i.e., half the quality) on some instances. |
Here is the code I used to generate the plots. You can freely copy and use it.
# MIT License
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.axes import Axes
def plot_performance_profile(
data: pd.DataFrame,
instance_column: str,
strategy_column: str,
metric_column: str,
direction: str,
comparison: str = "relative",
title: str | None = None,
highlight_best: bool = False,
ax: Axes | None = None,
scale: str | None = None,
log_base: int = 2,
figsize: tuple = (9, 6),
) -> Axes:
"""
Plot a performance profile, either on a relative-ratio basis or absolute-difference basis:
- For comparison="relative":
x-axis: performance ratio τ (log scale if τ_max > 10)
τ = (value / best) if direction="min", or τ = (best / value) if direction="max".
- For comparison="absolute":
x-axis: absolute difference Δ = (value - best) if direction="min",
or Δ = (best - value) if direction="max".
- y-axis: proportion of problems with τ (or Δ) ≤ x for each solver.
- If highlight_best=True, detect and bold the dominating solver curve (AUC in appropriate space).
- Ensures a reasonable number of ticks on the x-axis.
Args:
data: DataFrame with columns [instance, strategy, metric].
instance_column: column name identifying each problem instance.
strategy_column: column name identifying each solver/strategy.
metric_column: column name of the performance metric (e.g. runtime or cost).
direction: "min" if lower metric → better, "max" if higher → better.
comparison: "relative" or "absolute".
title: Optional plot title.
highlight_best: If True, find the solver with largest AUC and draw it in bold.
ax: An existing matplotlib Axes to draw into. If None, a new Figure+Axes will be created using figsize.
scale: x-axis scale override ("linear" or "log"); if None, chosen automatically.
log_base: base for log scale if used (default 2).
figsize: Tuple (width, height). Only used if ax is None.
Returns:
The matplotlib Axes containing the performance profile.
"""
if direction not in ("min", "max"):
raise ValueError("`direction` must be 'min' or 'max'.")
if comparison not in ("relative", "absolute"):
raise ValueError("`comparison` must be 'relative' or 'absolute'.")
# 1) Compute best value per instance
best_val = data.groupby(instance_column)[metric_column].agg(direction)
# 2) Pivot to get per-instance × per-strategy medians
pivot = (
data.groupby([instance_column, strategy_column])[metric_column]
.median()
.unstack(fill_value=np.nan)
)
# 3) Build comparison matrix C[p, s]
comp = pd.DataFrame(index=pivot.index, columns=pivot.columns, dtype=float)
if comparison == "relative":
for strat in pivot.columns:
if direction == "min":
comp[strat] = pivot[strat] / best_val
else: # direction == "max"
comp[strat] = best_val / pivot[strat]
comp = comp.replace([np.inf, -np.inf, 0.0], np.nan)
else: # comparison == "absolute"
for strat in pivot.columns:
if direction == "min":
comp[strat] = pivot[strat] - best_val
else: # direction == "max"
comp[strat] = best_val - pivot[strat]
comp = comp.replace([np.inf, -np.inf], np.nan)
# 4) Collect all distinct x-values (τ or Δ), including baseline
all_vals = comp.values.flatten()
finite_vals = all_vals[np.isfinite(all_vals)]
baseline = 1.0 if comparison == "relative" else 0.0
all_x = np.unique(np.sort(finite_vals))
all_x = np.concatenate(([baseline], all_x))
all_x = np.unique(np.sort(all_x))
# 5) Build performance-profile DataFrame ρ(x)
n_instances = comp.shape[0]
profile = pd.DataFrame(index=all_x, columns=comp.columns, dtype=float)
for x in all_x:
leq = (comp <= x).sum(axis=0)
profile.loc[x] = leq / n_instances
# 6) Identify dominating solver if requested (max AUC)
best_solver = None
if highlight_best:
if comparison == "relative":
# integrate ρ(τ) w.r.t. log(τ)
log_x = np.log(all_x)
areas = {}
for strat in profile.columns:
y = profile[strat].astype(float).values
areas[strat] = np.trapz(y, x=log_x)
best_solver = max(areas, key=areas.get)
else:
# integrate ρ(Δ) w.r.t. Δ
areas = {}
for strat in profile.columns:
y = profile[strat].astype(float).values
areas[strat] = np.trapz(y, x=all_x)
best_solver = max(areas, key=areas.get)
# 7) Create or use existing Axes
if ax is None:
fig, ax = plt.subplots(figsize=figsize)
else:
fig = ax.figure
# 8) Determine scale if not overridden
if scale is None:
if comparison == "relative" and all_x[-1] > 10:
use_log = True
else:
use_log = False
else:
use_log = scale == "log"
# 9) Plot each solver’s curve
for strat in profile.columns:
y = profile[strat].astype(float)
if highlight_best and strat == best_solver:
ax.step(all_x, y, where="post", label=strat, linewidth=3.0, alpha=1.0)
else:
ax.step(
all_x,
y,
where="post",
label=strat,
linewidth=1.5,
alpha=0.6 if highlight_best else 1.0,
)
# 10) Axis scaling and limits
if comparison == "relative":
if use_log:
ax.set_xscale("log", base=log_base)
ax.set_xlim(all_x[1], all_x[-1] * 1.1)
else:
ax.set_xscale("linear")
ax.set_xlim(1.0, all_x[-1] * 1.1)
xlabel = (
f"Within this factor of the best (log{log_base} scale)"
if use_log
else "Within this factor of the best (linear scale)"
)
else: # absolute
ax.set_xscale("linear")
ax.set_xlim(0.0, all_x[-1] * 1.1)
xlabel = "Absolute difference from the best"
ax.set_ylim(0.0, 1.02)
ax.set_xlabel(xlabel, fontsize=12)
ax.set_ylabel("Proportion of problems", fontsize=12)
if title:
ax.set_title(title, fontsize=14, pad=14)
else:
ax.set_title("Performance Profile", fontsize=14, pad=14)
ax.axvline(x=baseline, color="gray", linestyle="--", alpha=0.7)
ax.grid(True, which="both", linestyle=":", linewidth=0.5)
# 11) Legend inside lower right
ax.legend(loc="lower right", frameon=False)
fig.tight_layout()
return ax
 Tangi Migot has written an excellent article on Performance Plots. Also take a look on the original paper Benchmarking optimization software with performance profiles (Dolan & Moré 2002) |
Analyzing the Scalability of a Single Model
When working with a single model and aiming to analyze its scalability, a split plot can serve as an effective visualization. This type of plot shows the model’s runtime across instances of varying size, under a fixed time limit. If an instance is solved within the time limit, its actual runtime is shown. If not, the point is plotted above the time limit on a transformed y-axis that now displays the optimality gap instead of runtime.
An example of such a plot is shown below. Since aggregating this data into a line plot can be challenging, the visualization may become cluttered if too many instances are included or if multiple models are compared simultaneously.
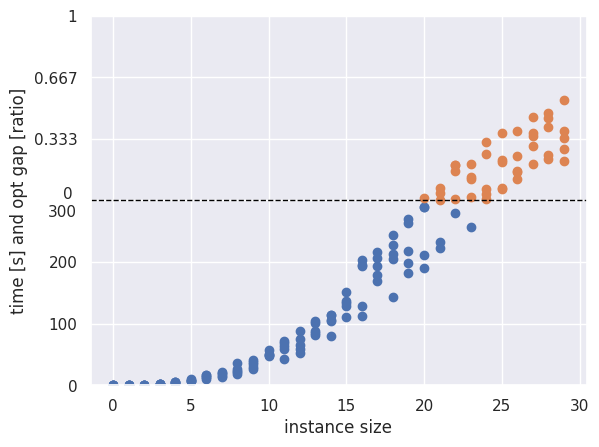 |
|---|
| Split plot illustrating runtime (for solved instances) and optimality gap (for unsolved instances). The y-axis is divided into two regions: one showing actual runtimes for instances solved within the time limit, and one showing optimality gaps for instances where the time limit was exceeded. |
 For many problems, there is no single instance size metric to compare over. Usually, you can still classify the instances into size categories. However, for especially complex problems, it may be best to just provide a table with the results for the largest instances to give an idea of the model’s scalability. |
Importance of Including Tables
Tables offer a concise and detailed view of benchmarking results. They allow readers to verify the accuracy of reported data, inspect individual instances, and complement high-level visual summaries such as plots.
While the previous sections presented insightful plots for visualizing performance trends, it is essential to also include at least one table that contains the raw results for the key benchmark instances. Many high-quality papers rely solely on tables to present their results, as they provide transparency and precision.
However, avoid including every table with all available data—this applies even to appendices. Instead, consider what information a critical reader would need to verify that your plots are not misleading. Focus on presenting the most relevant and interpretable results. A comprehensive dataset can always be linked in an external repository, but the tables within your paper should remain clear, selective, and to the point. Even if you are only optimizing for yourself, use plots to gain an overview but also check out the data tables.
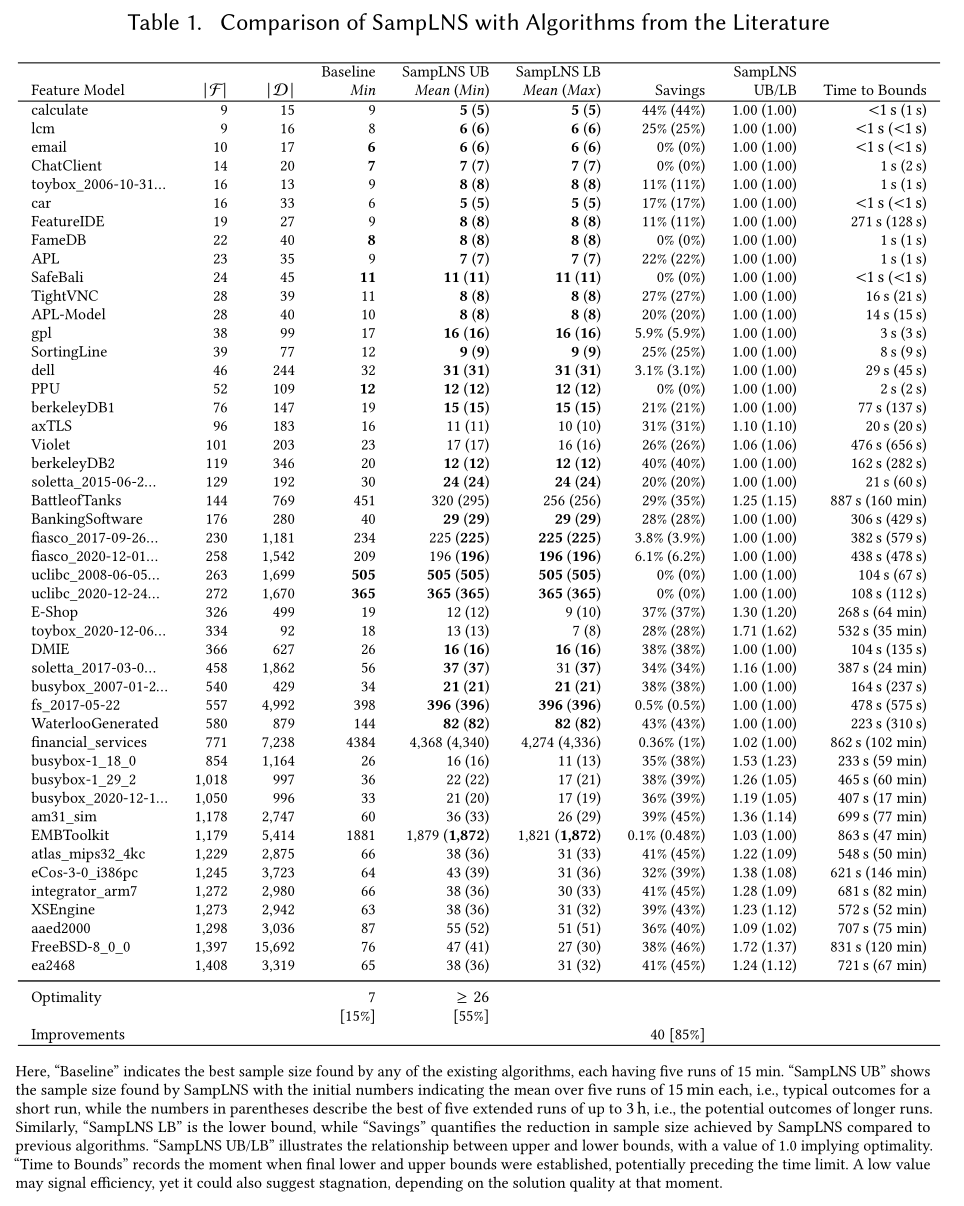 |
|---|
| Example table from a recent publication, presenting detailed results of a new algorithm across benchmark instances. While less intuitive than plots, such tables enable readers to examine individual outcomes in detail. |
Distinguishing Exploratory and Workhorse Studies in Benchmarking
Before diving into comprehensive benchmarking for scientific publications, it is essential to conduct preliminary investigations to assess your model’s capabilities and identify any foundational issues. This phase, known as exploratory studies, is crucial for establishing the basis for more detailed benchmarking, subsequently termed as workhorse studies. These latter studies aim to provide reliable answers to specific research questions and are often the core of academic publications. It is important to explicitly differentiate between these two study types and maintain their distinct purposes: exploratory studies for initial understanding and flexibility, and workhorse studies for rigorous, reproducible research.
 For a comprehensive exploration of benchmarking, I highly recommend Catherine C. McGeoch’s book, “A Guide to Experimental Algorithmics”, which offers an in-depth discussion on this topic. |
Exploratory Studies: Foundation Building
Exploratory studies serve as a first step toward understanding both your model and the problem it aims to solve. This phase is focused on building intuition and identifying key characteristics before committing to formal benchmarking.
- Objective: The goal at this stage is to gain early insights — not to draw definitive conclusions. Exploratory studies help identify realistic instance sizes, anticipate potential challenges, and narrow down hyperparameter search spaces.
Avoid setting up elaborate benchmarking frameworks during this phase. Keep the process lightweight and flexible to enable rapid iteration. If updating your benchmarks becomes cumbersome each time you adjust your model, it will slow your progress and — since benchmarking code tends to be tedious — you may lose motivation quickly.
From personal experience, I observed a significant drop in productivity when I first learned to build robust benchmarking setups. I began applying the same level of rigor to exploratory phases, mistakenly treating the setup as a one-off investment that would pay off in the long run. However, whenever you do something genuinely interesting, unexpected issues inevitably arise, requiring further iterations on the setup. In trying to anticipate such surprises, it becomes tempting to over-engineer the process—spending excessive time considering what could go wrong and preparing for every contingency, rather than simply getting started.
Instead, strike a balance: avoid letting things become disorganized, but postpone formal benchmarking until you are ready to share results. For example, I used quick exploratory studies in a single jupyter notebook to estimate appropriate instance sizes for the benchmark plots shown earlier. Not a reliable part of a pipeline, but it got the job done quickly and only then I set up a proper pipeline to create my final plots and tables.
Workhorse Studies: Conducting In-depth Evaluations
Workhorse studies follow the exploratory phase and are characterized by more structured and meticulous methodologies. This stage is essential for conducting comprehensive evaluations of your model and collecting substantive data for analysis.
- Objective: These studies aim to answer specific research questions and yield meaningful insights. The approach is methodical, emphasizing clearly defined objectives. Benchmarks should be well-structured and sufficiently large to produce statistically significant results.
While you can convert one of your exploratory studies into a workhorse study, I strongly recommend starting the data collection process from scratch. Make it as difficult as possible for outdated or flawed data to enter your benchmarking setup.
Your exploratory studies should already have provided a reasonable estimate of the required runtime for benchmarks. Always ensure that you allocate sufficient time for potential failures and that your setup can resume if, for instance, a colleague inadvertently terminates your job. Monitor the results while the benchmarks are running—you do not want to wait a week only to discover that you forgot to save the solutions.
I personally structure a workhorse study as follows:
-
Hypothesis or Research Question Clearly define a hypothesis or research question that emerged during the exploratory phase.
-
Experiment Design Develop a detailed experimental plan, including the instance set, the models/configurations to be evaluated, and the metrics to be collected.
-
Benchmark Setup Implement a robust benchmarking framework that supports reproducibility and efficient execution.
-
Data Collection Execute the experiments, ensuring that all relevant data is collected and stored in a structured and reliable format.
-
Data Analysis Analyze the results using appropriate statistical and visualization techniques.
-
Discussion of Findings Interpret the results and discuss their implications in the context of the initial hypothesis or research question.
-
Threats to Validity Reflect on potential threats to the validity of your findings, such as biases in instance selection, model assumptions, or evaluation procedures.
Selecting a Benchmark Instance Set
Constructing a benchmark instance set is often more challenging than it first appears, especially when no established benchmarks exist. Even when such sets exist, they may be poorly sized or less realistic than anticipated. In fact, some seemingly realistic datasets may have had portions of the original data replaced with uniformly random values to preserve confidentiality, often without realizing that such modifications can substantially alter the problem’s characteristics. Crafting a high-quality benchmark instance set can be an art in itself. A notable example is the MIPLIB collection, which stands as a scientific contribution in its own right.
If you already have a deployed implementation, the process is fortunately quite straightforward. You can collect the instances that have been solved in the past and use them (or a representative subset) as your benchmark set. Performing basic data analysis to examine the distribution of instance characteristics is advisable; for example, it may turn out that 99% of the instances are trivial, while the remaining 1% are significantly more challenging and thus more relevant for improvement. In most cases, basic domain knowledge and judgment are often sufficient to construct a useful benchmark set without the need for particularly creative solutions.
If you are not in this fortunate position, the first step is to check whether any public data is available for your problem or for a sufficiently similar one. For instance, although the widely used TSPLIB benchmark set for the Traveling Salesman Problem (TSP) contains only distance information, it is relatively straightforward to generate Capacitated Vehicle Routing Problem (CVRP) instances from it, allowing the reuse of well-structured and challenging inputs for a related problem. This can be done by randomly selecting a depot and assigning a vehicle capacity based on a fraction of a heuristic TSP solution. If you obtain readily available instances, be sure to verify whether they remain challenging; they may originate from a different era or may not have been well-designed, as not everything published online is of high quality (although I hope that this Primer is).
If no suitable public benchmarks are available, you will need to generate your own instances. Even with public benchmarks available, generating your own instances can still be beneficial to generate additional instances in order to control specific parameters and systematically evaluate the impact of varying a single factor on your model’s performance. In typical benchmark sets, the diverse instances can confound the effects of individual parameters, making it difficult to isolate their impact without large datasets and careful statistical design. Nevertheless, it is important to maintain diversity within your general instance set to ensure that your model remains robust and capable of handling a broad range of scenarios.
|
To deepen your understanding of benchmark instance diversity, consider the concept of Instance Space Analysis. Kate Smith-Miles offers an insightful 30-minute talk on this topic, exploring how analyzing the space of instances can guide better instance selection and generation.  |
When implementing your own instance generation, it is often possible to leverage existing tools. For example, NetworkX provides a comprehensive collection of random graph generators that can be adapted to suit a variety of problem settings. An exploratory study is usually necessary to identify which generator aligns best with the requirements of your specific problem. For generating other types of values, you can experiment with different random distributions. One particularly effective technique is using images to define spatial or value distributions, for example, treating pixel intensities as sampling probabilities.
 It is also advisable not to combine all your instances into a single set, but instead to evaluate performance separately across different benchmark groups. This approach often reveals interesting and meaningful performance differences. |
A final point worth emphasizing is the importance of generating and storing proper instance files, rather than relying solely on the seed of a pseudo-random number generator. This is a recurring concern I have encountered with both experienced peers and students. While pseudo-random generators are valuable for introducing randomized but reproducible elements into algorithms, they are not a substitute for persistently stored data. (That said, I have seen too many cases where a student unknowingly computed the mean over multiple runs using the same seed.) Although, in theory, a seed combined with the source code should suffice to reproduce a complete experiment, in practice, code tends to degrade more quickly than data. This is especially true for C++ code, which may be less reproducible than anticipated due to subtle instances of undefined behavior, even among experienced programmers.
Efficiently Managing Your Benchmarks
Benchmark data management can quickly become complex, especially when managing multiple experiments and research questions simultaneously. The following strategies can help maintain an organized workflow and ensure that your results remain reliable:
-
Folder Structure: Maintain a clear and consistent folder hierarchy for your experiments. A typical setup includes a top-level
evaluationsdirectory with descriptive subfolders for each experiment. For example:evaluations ├── tsp │ ├── 2023-11-18_random_euclidean │ │ ├── PRIVATE_DATA │ │ │ ├── ... all data for debugging and internal use │ │ ├── PUBLIC_DATA │ │ │ ├── ... curated data intended for sharing │ │ ├── _utils # optional │ │ │ ├── ... shared utility functions to keep top level clean │ │ ├── README.md # Brief description of the experiment │ │ ├── 00_generate_instances.py │ │ ├── 01_run_experiments.py │ │ ├── ... │ ├── 2023-11-18_tsplib │ │ ├── PRIVATE_DATA │ │ │ ├── ... debugging data │ │ ├── PUBLIC_DATA │ │ │ ├── ... selected shareable data │ │ ├── README.md │ │ ├── 01_run_experiments.py │ │ ├── ... -
Documentation: It is easy to forget why or when a particular experiment was conducted. Always include a brief
README.mdfile with essential notes. This document does not need to be polished initially, but it should capture the core context. The more important the experiment, the more beneficial it is to revisit and enhance the documentation once the experiment is underway and you have had time to reflect on its purpose and outcomes. -
Redundancy: Excessive concern about redundancy in your data and code is generally unnecessary. Evaluation setups are not production systems and are not expected to be maintained over the long term. In fact, redundancy, particularly in utility functions, can simplify refactoring. Legacy experiments can continue using older versions of the code, and updates can be applied selectively. It is advisable to include a brief changelog in each utility file to indicate the version in use. Consider this a lightweight form of dependency management. Although copying and pasting code may feel inappropriate to a software engineer trained in best practices, this portion of your work is typically intended to be static for reproducibility, rather than actively maintained.
-
Extensive Private and Simple Public Data: Organize your data into two sections: one for private use and one for public dissemination. The private section should contain all raw and intermediate data to facilitate future investigations into anomalies or unexpected behavior. The public section should be concise, curated, and optimized for analysis and sharing. If the private data grows too large, consider transferring it to external storage and leaving a reference or note indicating its location, ideally with the hope that it will not be needed again. If your experiments are not huge, you may also be able to store all data in the public section.
-
Experiment Flexibility: Design experiments to be both interruptible and extensible. This allows long-running studies to be paused and resumed, and new models or configurations to be added without restarting the entire process. Such flexibility is particularly valuable in exploratory research, which often involves frequent iterations, as well as in large-scale, long-duration runs. The longer an experiment runs, the more likely it is that it will be interrupted by system updates, network failures, or other unforeseen events.
-
Parallelization: Obtaining results quickly can help maintain momentum and focus. Learn to utilize a computing cluster or cloud infrastructure to parallelize experiments. Although there is an initial learning curve, the effort required to implement parallelization is usually small in comparison to the efficiency gains it provides.
 Because existing tools did not fully satisfy my requirements, I developed AlgBench to manage benchmarking results and Slurminade to simplify experiment distribution on computing clusters through a decorator-based interface. However, more effective solutions may now be available, particularly from the machine learning community. If you are aware of tools you find useful, I would be very interested in hearing about them and would be glad to explore their potential. |
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.

