The CP-SAT Primer - Using and Understanding Google OR-Tools' CP-SAT Solver

Benchmarking your Model

This chapter explores methods for comparing the performance of different models applied to complex problems, where the basic model leaves room for improvement — either in runtime or in solution quality, especially when the model cannot always be solved to optimality. As a scientist writing a paper on a new model (or, more likely, a new algorithm that internally uses a model), this will be the default case as research on a problem that can already be solved well is hard to publish. Whether you aim merely to evaluate whether your new approach outperforms the current one or intend to prepare a formal scientific publication, you face the same challenges; in the latter case, however, the process becomes more extensive and formalized (but this may also be true for the first case depending on your manager).

In some cases, the primary performance bottleneck may not lie within CP-SAT itself but rather in the Python code used to generate the model. Identifying the most resource-intensive segments of your Python code is therefore essential. The profiler Scalene has proven to be particularly effective for diagnosing such issues. That said, in many situations, simple logging statements — e.g., logging.info("Building circuit constraint on graph with %d nodes and %d edges", n, m) — can be sufficient to reveal performance problems. It is easy to underestimate the size or construction cost of auxiliary structures, which can have a significant impact on overall runtime.

During the explorative phase, when you probe different ideas, you will likely select one to five instances that you can run quickly and compare. However, for most applications, this number is insufficient, and you risk overfitting your model to these instances — gaining performance improvements on them but sacrificing performance on others. You may even limit your model’s ability to solve certain instances.

A classic example involves deactivating specific CP-SAT search strategies or preprocessing steps that have not yielded benefits on the selected instances. If your instance set is large enough, the risk is low; however, if you have only a few instances, you may remove the single strategy necessary to solve a particular class of problems. Modern solvers include features that impose a modest overhead on simple instances but enable solving otherwise intractable cases. This trade-off is worthwhile: do not sacrifice the ability to solve complex instances for a marginal performance gain on simple ones. Therefore, always benchmark your changes properly before deploying them to production, even if you do not plan to publish your results scientifically.

No-Free-Lunch Theorem and Timeouts

The no‐free‐lunch theorem and timeouts complicate benchmarking more than you might have anticipated. The no‐free‐lunch theorem asserts that no single algorithm outperforms all others across every instance, which is especially true for NP‐hard problems. Consequently, improving performance on some instances often coincides with degradations on others. It is essential to assess whether the gains justify the losses.

Another challenge arises when imposing a time limit to prevent any individual instance from running indefinitely; without it, benchmarks can take prohibitively long. Yet comparing aborted runs to those that complete within the time limit poses a dilemma: disqualifying models that time out may leave no viable candidate, since with sufficient instances, any solver will be unlucky at least once. Thus, simple exclusion is not an option for most applications. Timeouts introduce "unknowns" into your results: a solver might have succeeded given just one more millisecond, or it might have been trapped in an endless loop. This uncertainty complicates the computation of accurate statistics.

Example: Nurse Rostering Problem Benchmark

Let us examine the performance of CP-SAT, Gurobi, and Hexaly on a Nurse Rostering Problem. Nurse rostering is a complex yet common problem in which nurses must be assigned to shifts while satisfying a variety of constraints. Since CP-SAT, Gurobi, and Hexaly differ significantly in their underlying algorithms, the comparison reveals pronounced performance differences. However, such patterns can also be observed when using the same solver across instances, albeit usually not as pronounced.

The following two plots illustrate the value of the incumbent solution (i.e., the best solution found so far) and the best proven lower bound during the search. These are challenging instances, and only Gurobi is able to find an optimal solution.

Notably, the best-performing solver changes depending on the allotted computation time. For this problem, Hexaly excels at finding good initial solutions quickly but tends to stall thereafter. CP-SAT requires slightly more time to get started but demonstrates steady progress. In contrast, Gurobi begins slowly but eventually makes substantial improvements.

So, which solver is best for this problem?

Performance comparison of CP-SAT, Gurobi, and Hexaly on instance 19 of the Nurse Rostering Problem Benchmark. Hexaly starts strong but is eventually overtaken by CP-SAT. Gurobi surpasses Hexaly near the end by a small margin. CP-SAT and Gurobi converge to nearly the same lower bound.

Performance comparison of CP-SAT, Gurobi, and Hexaly on instance 20 of the Nurse Rostering Problem Benchmark. Hexaly again performs well early but is outperformed by CP-SAT. Gurobi maintains a poor incumbent value for most of the runtime but eventually makes a significant improvement and proves optimality. The optimal solution is visibly superior to CP-SAT's best solution. CP-SAT is unable to prove a meaningful lower bound for this instance.

These two plots — and even this specific problem — are insufficient to draw definitive conclusions about the overall performance of the solvers. Nevertheless, it is remarkable that our beloved open-source solver, CP-SAT, performs so well against the commercial solvers Gurobi and Hexaly in this context.

If provably optimal solutions are required, Gurobi may be the most suitable choice; however, the likelihood of achieving optimality is low for most instances. If your instances are expected to grow in size and require fast solutions, Hexaly might be preferable, as it appears highly effective at finding good solutions quickly. This observation is also supported by preliminary results on larger instances, for which neither CP-SAT nor Gurobi find any feasible solution. CP-SAT, by contrast, offers a strong compromise between the two: although it starts more slowly, it maintains consistent progress throughout the search.

A commonly used metric for convergence is the primal integral, which measures the area under the curve of the incumbent solution value over time. It provides a single scalar that summarizes how quickly a solver improves its best-known solution. CP-SAT reports a related metric: the integral of the logarithm of the optimality gap, which also accounts for the quality of the bound. These metrics offer an objective measure of solver progress over time, though they may not fully capture problem-specific or subjective priorities.

Defining Your Benchmarking Goals

The first step is to determine your specific requirements and how best to measure solver performance accordingly. It is not feasible to manually plot performance for every instance and assign scores based on subjective impressions; such an approach does not scale and lacks objectivity and reproducibility. Instead, you should define a concrete metric that accurately reflects your goals. One strategy is to carefully select benchmark instances that are still likely to be solved to optimality, with the expectation that performance trends will generalize to larger instances. Another to decide for a fixed time limit we are willing to wait for a solution, and then measure how well each solver performs under these constraints. While no evaluation method will be perfect, it is essential to remain aware of potential threats to the validity of your results. Let us go through some common scenarios.

Use the SIGPLAN Empirical Evaluation Checklist if your evaluation has to satisfy academic standards.

Empirical studies on algorithms have historically faced some tension within the academic community, where theoretical results are often viewed as more prestigious or fundamental. The paper Needed: An Empirical Science of Algorithms by John Hooker (1994) offers a valuable historical and philosophical perspective on this issue.

Common Benchmarking Scenarios

Several common benchmarking scenarios arise in practice. To choose the appropriate visualization or evaluation method, it is useful to take a moment to identify which scenario applies to your case—and to recognize which tools are best suited to other situations. Do not simply go for the prettiest and most complex plot; instead, select the one that best fits your needs.

1. Instances are always solved to optimality, and only runtime matters. This is the simplest benchmarking scenario. If every instance can be solved to optimality and your only concern is runtime, you can summarize performance using the mean runtime or visualize it using a basic box plot. The primary challenge here lies in choosing the appropriate type of mean (e.g., arithmetic, geometric, harmonic) and selecting representative instances that reflect production-like conditions. For this case, the rest of the chapter may be skipped.

2. Optimal or feasible solutions are sought, but may not always be found within the time limit. When timeouts occur, runtimes for unsolved instances become unknown, making traditional means unreliable. In such cases, cactus plots are an effective way to visualize solver performance, even in the presence of incomplete data.

3. The goal is to find the best possible solution within a fixed time limit. Here, the focus is on solution quality under time constraints, rather than on whether optimality is reached. Performance plots are especially suitable for this purpose, as they reveal how closely each solver or model approaches the best-known solution across the benchmark set.

4. Scalability analysis: how performance evolves with instance size. If you are analyzing how well a model scales—i.e., how large an instance it can solve to optimality and how the optimality gap grows thereafter—split plots are a good choice. They show runtime for solved instances and optimality gap for those that exceed the time limit, allowing for a unified view of scalability.

5. Multi-metric performance comparison against a baseline. When you want a quick, intuitive overview of how your model performs across several metrics—such as runtime, objective value, and lower bound—scatter plots with performance zones are ideal. They provide a clear comparative visualization, making it easy to spot outliers and trade-offs across dimensions.

Quickly Comparing to a Baseline Using Scatter Plots

Scatter plots with performance zones are, in my experience, highly effective for quickly comparing the performance of a prototype against a baseline across multiple metrics. While these plots do not provide a formal quantitative evaluation, they offer a clear visual overview of how performance has shifted. Their key advantages are their intuitive readability and their ability to accommodate NaN values. They are particularly useful for identifying outliers, though they can be less effective when too many points overlap or when data ranges vary significantly.

Consider the following example table, which compares a basic optimization model with a prototype model in terms of runtime, objective value, and lower bound. The runtime is capped at 90 seconds, and if no optimal solution is found within this limit, the objective value is set to NaN. A run only terminates before the time limit if an optimal solution is found.

From the table, we can already spot some fundamental issues — for example, the prototype fails on three instances, and several instances yield significantly worse results than the baseline. However, when we turn to the scatter plots with performance zones, such anomalies become immediately apparent.

Scatter plot comparing the performance of a prototype model against a baseline model across three metrics: runtime, objective value, and lower bound. The x-axis represents the baseline model's performance; the y-axis shows the prototype model's performance. Color-coded zones indicate relative performance levels, making it easier to identify where the prototype outperforms or underperforms the baseline.

For runtime, both models typically hit the time limit, so there is limited variation to observe. However, the baseline model solves a few instances significantly faster, whereas the prototype consistently uses the full time limit. For the objective value, both models produce similar results on most instances. Yet, particularly on the larger instances, the prototype yields either very poor or no solutions at all.

Interestingly, the lower bounds produced by the prototype are much better for some instances. This improvement was not obvious from a cursory review of the table but becomes immediately noticeable in the plots.

Scatter plots are also highly effective when working with multiple performance metrics, particularly when you want to ensure that gains in one metric do not come at the expense of unacceptable losses in another. In practice, it is often difficult to precisely quantify the relative importance of each metric from the outset. The intuitive nature of these plots offers a valuable overview, serving as a visual aid before you commit to a specific performance metric. The example below illustrates a hypothetical scenario involving a vehicle routing problem.

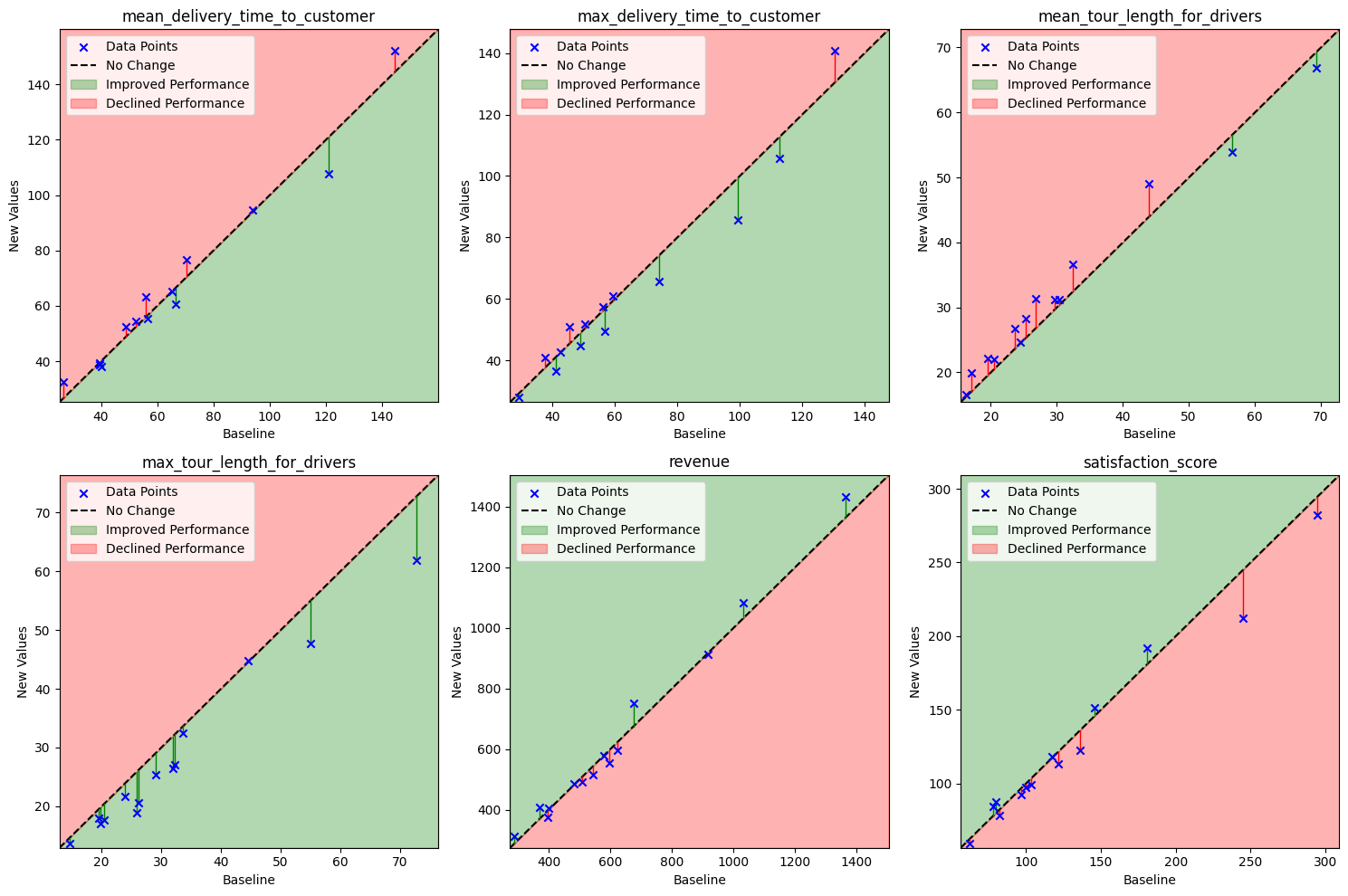Scatter plots illustrating performance trade-offs across multiple metrics in a hypothetical vehicle routing problem. These plots help assess whether improvements in one metric come at the cost of significant regressions in another. Their intuitive layout makes them especially useful when metric priorities are not yet clearly defined, offering a quick overview of relative performance and highlighting outliers across different algorithm versions.

"""
This module contains functions to plot a scatter comparison of baseline and new values with performance areas highlighted.

You can freely use and distribute this code under the MIT license.

Changelog:
    2024-08-27: First version
    2024-08-29: Added lines to the diagonal to help with reading the plot
    2025-06-07: Basic improvements and fixing issue with index comparison.

(c) 2025 Dominik Krupke, https://github.com/d-krupke/cpsat-primer
"""

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd


def plot_performance_scatter(
    ax,
    baseline: pd.Series,
    new_values: pd.Series,
    lower_is_better: bool = True,
    title: str = "",
    **kwargs,
):
    """
    Plot a scatter comparison of baseline and new values with performance areas highlighted.

    Parameters:
        ax (matplotlib.axes.Axes): The axes on which to plot.
        baseline (pd.Series): Series of baseline values.
        new_values (pd.Series): Series of new values.
        lower_is_better (bool): If True, lower values indicate better performance.
        title (str): Title of the plot.
        **kwargs: Additional keyword arguments for customization (e.g., 'color', 'marker').
    """
    if not isinstance(baseline, pd.Series) or not isinstance(new_values, pd.Series):
        raise ValueError("Both baseline and new_values should be pandas Series.")
    if baseline.size != new_values.size:
        raise ValueError("Both Series should have the same length.")

    scatter_kwargs = {
        "color": kwargs.get("color", "blue"),
        "marker": kwargs.get("marker", "x"),
        "label": kwargs.get("label", "Data Points"),
    }

    line_kwargs = {
        "color": kwargs.get("line_color", "k"),
        "linestyle": kwargs.get("line_style", "--"),
        "label": kwargs.get("line_label", "No Change"),
    }

    fill_improve_kwargs = {
        "color": kwargs.get("improve_color", "green"),
        "alpha": kwargs.get("improve_alpha", 0.3),
        "label": kwargs.get("improve_label", "Improved Performance"),
    }

    fill_decline_kwargs = {
        "color": kwargs.get("decline_color", "red"),
        "alpha": kwargs.get("decline_alpha", 0.3),
        "label": kwargs.get("decline_label", "Declined Performance"),
    }

    # Replace inf values with NaN
    baseline = baseline.replace([np.inf, -np.inf], np.nan)
    new_values = new_values.replace([np.inf, -np.inf], np.nan)

    max_val = max(baseline.max(skipna=True), new_values.max(skipna=True)) * 1.05
    min_val = min(baseline.min(skipna=True), new_values.min(skipna=True)) * 0.95

    # get indices of NA values
    na_indices = baseline.isna() | new_values.isna()

    if lower_is_better:
        # replace NA values with max_val
        baseline = baseline.fillna(max_val)
        new_values = new_values.fillna(max_val)
    else:
        # replace NA values with min_val
        baseline = baseline.fillna(min_val)
        new_values = new_values.fillna(min_val)

    # plot the na_indices with a different marker
    if na_indices.any():
        ax.scatter(
            baseline[na_indices],
            new_values[na_indices],
            marker="s",
            color=scatter_kwargs["color"],
            label="N/A Values",
            zorder=2,
        )

    # add the rest of the data points
    ax.scatter(
        baseline[~na_indices], new_values[~na_indices], **scatter_kwargs, zorder=2
    )

    ax.plot([min_val, max_val], [min_val, max_val], zorder=1, **line_kwargs)

    x = np.linspace(min_val, max_val, 500)
    if lower_is_better:
        ax.fill_between(x, min_val, x, zorder=0, **fill_improve_kwargs)
        ax.fill_between(x, x, max_val, zorder=0, **fill_decline_kwargs)
    else:
        ax.fill_between(x, x, max_val, zorder=0, **fill_improve_kwargs)
        ax.fill_between(x, min_val, x, zorder=0, **fill_decline_kwargs)

    # draw thin lines to the diagonal to help with reading the plot.
    # A problem without lines is that one tends to use the distance
    # to the diagonal as a measure of performance, which is not correct.
    # Instead, it is `y-x` that should be used.
    for old_val, new_val in zip(baseline, new_values):
        if pd.isna(old_val) and pd.isna(new_val):
            continue
        if pd.isna(old_val):
            old_val = min_val if lower_is_better else max_val
        if pd.isna(new_val):
            new_val = min_val if lower_is_better else max_val
        if lower_is_better and new_val < old_val:
            ax.plot(
                [old_val, old_val],
                [old_val, new_val],
                color="green",
                linewidth=1.0,
                zorder=1,
            )
        elif not lower_is_better and new_val > old_val:
            ax.plot(
                [old_val, old_val],
                [old_val, new_val],
                color="green",
                linewidth=1.0,
                zorder=1,
            )
        elif lower_is_better and new_val > old_val:
            ax.plot(
                [old_val, old_val],
                [old_val, new_val],
                color="red",
                linewidth=1.0,
                zorder=1,
            )
        elif not lower_is_better and new_val < old_val:
            ax.plot(
                [old_val, old_val],
                [old_val, new_val],
                color="red",
                linewidth=1.0,
                zorder=1,
            )

    ax.set_xlim(min_val, max_val)
    ax.set_ylim(min_val, max_val)
    ax.set_xlabel(kwargs.get("xlabel", "Baseline"))
    ax.set_ylabel(kwargs.get("ylabel", "New Values"))
    if title:
        ax.set_title(title)
    ax.legend()


def plot_comparison_grid(
    baseline_data: pd.DataFrame,
    new_data: pd.DataFrame,
    metrics: list[tuple[str, str]],
    n_cols: int = 4,
    figsize: tuple[int, int] | None = None,
    suptitle: str = "",
    subplot_kwargs: dict | None = None,
    **kwargs,
):
    """
    Plot a grid of performance comparisons for multiple metrics.

    Parameters:
        baseline_data (pd.DataFrame): DataFrame containing the baseline data.
        new_data (pd.DataFrame): DataFrame containing the new data.
        metrics (list of tuple of str): List of tuples containing column names and comparison direction ('min' or 'max').
        n_cols (int): Number of columns in the grid.
        figsize (tuple of int): Figure size (width, height).
        suptitle (str): Title for the entire figure.
        **kwargs: Additional keyword arguments to pass to individual plot functions.

    Returns:
        fig (matplotlib.figure.Figure): The figure object containing the plots.
        axes (np.ndarray): Array of axes objects corresponding to the subplots.
    """
    n_metrics = len(metrics)
    n_cols = min(n_cols, n_metrics)
    n_rows = (n_metrics + n_cols - 1) // n_cols  # Ceiling division

    # Validate columns and directions
    for column, direction in metrics:
        if direction not in {"min", "max"}:
            raise ValueError("The direction should be either 'min' or 'max'.")
        if column not in baseline_data.columns or column not in new_data.columns:
            raise ValueError(f"Column '{column}' not found in the data.")

    # Validate index alignment
    if set(baseline_data.index) != set(new_data.index):
        raise ValueError("Indices of the DataFrames do not match (different values).")


    if figsize is None:
        figsize = (5 * n_cols, 5 * n_rows)

    fig, axes = plt.subplots(n_rows, n_cols, figsize=figsize)
    axes = axes.flatten()

    for ax, (column_name, direction) in zip(axes, metrics):
        # Merge kwargs and subplot_kwargs[column_name] (if present) into a new dict
        merged_kwargs = dict(kwargs)
        if subplot_kwargs and column_name in subplot_kwargs:
            merged_kwargs.update(subplot_kwargs[column_name])
        plot_performance_scatter(
            ax,
            baseline_data[column_name],
            new_data[column_name],
            lower_is_better=(direction == "min"),
            title=column_name,
            **merged_kwargs,
        )

    # Turn off any unused subplots
    for ax in axes[n_metrics:]:
        ax.axis("off")

    if suptitle:
        fig.suptitle(suptitle, fontsize=16)

    plt.tight_layout(rect=[0, 0, 1, 0.96])

    return fig, axes

Success-Based Benchmarking: Cactus Plots and PAR Metrics

The SAT community frequently uses cactus plots (also known as survival plots) to effectively compare the time to success of different solvers on a benchmark set, even when timeouts occur. If you are dealing with a pure constraint satisfaction problem, this approach is directly applicable. However, it can also be extended to other binary success indicators — such as proving optimality, even under optimality tolerances.

Additionally, the PAR10 metric is commonly used to summarize solver performance on a benchmark set. It is defined as the average time a solver takes to solve an instance, where unsolved instances (within the time limit) are penalized by assigning them a runtime equal to 10 times the cutoff. Variants like PAR2, which use a penalty factor of 2 instead of 10, are also encountered. While a factor of 10 is conventional, it remains an arbitrary choice. Ultimately, you must decide how to handle unknowns—instances not solved within the time limit—since you only know that their actual runtime exceeds the cutoff. If an explicit performance metric is required to declare a winner, PAR-style metrics are widely accepted but come with notable limitations.

To gain a more nuanced view of solver performance, cactus plots are often employed. In these plots, each solver is represented by a line where each point \( (x, y) \) indicates that \( x \) benchmark instances were solved within \( y \) seconds.

Each point \( (x, y) \) shows that \( x \) instances were solved within \( y \) seconds.

The mean PAR10 scores for the four strategies in the example above are as follows:

In case you are wondering, this is some data on solving the Traveling Salesman Problem (TSP) with different strategies. Gurobi dominates, but it is well-known that Gurobi is excellent at solving TSP.

If the number of solvers or models under comparison is not too large, you can also use a variation of the cactus plot to show solver performance under different optimality tolerances. This allows you to examine how much performance improves when the tolerance is relaxed. However, if your primary interest lies in solution quality, performance plots are likely to be more appropriate.

In the following example, different optimality tolerances reveal a visible performance improvement for the strategies AddCircuit and Miller-Tucker-Zemlin. For the other two strategies, the impact of tolerance changes is minimal. This variation of the cactus plot can also be applied to compare solver performance across different benchmark sets, especially if you suspect significant variation across instance categories.

Each line style represents an optimality tolerance. The plot shows how many instances (\( y \)) can be solved within a given time limit (\( x \)) for each tolerance.

It is also common practice to include a virtual best line in the cactus plot. This line indicates, for each instance, the best time achieved by any solver. Although it does not represent an actual solver, it serves as a valuable reference to evaluate the potential for solver complementarity. If one solver clearly dominates, the virtual best line will coincide with its curve. However, if the lines diverge, it suggests that no single solver is universally superior—a case of the “no free lunch” principle. Even if one solver performs best on 90% of instances, the remaining 10% may be better handled by alternatives. The greater the gap between the best actual solver and the virtual best, the stronger the case for a portfolio approach.

A more detailed discussion on this type of plot can be found in the referenced academic paper: Benchmarking Solvers, SAT-style by Brain, Davenport, and Griggio

Performance Plots for Solution Quality within a Time Limit

When dealing with instances that typically cannot be solved to optimality, performance plots are often more appropriate than cactus plots. These plots illustrate the relative performance of different models or solvers on a set of instances, usually under a fixed time limit. At the leftmost point of the plot (where \( x = 1 \)), each solver’s line indicates the proportion of instances for which it achieved the best-known solution (not necessarily exclusively). Then its \( (x,y) \) coordinates indicate the proportion \( y \) of instances for which the solver achieved a solution that is at most \( x \) times worse than the best known solution. For example, if a solver has a point at \( (1.05, 0.8) \), it means that it found a solution within 5% of the best-known solution for 80% of the instances. The x-axis is usually on a logarithmic scale, allowing for a more detailed view of the performance differences. Often, a logarithmic scale is used for the x-axis, especially when the performance ratios vary widely. However, down below we use a linear scale because the values are close to 1.

In the example below, based on the Capacitated Vehicle Routing Problem (CVRP), the performance plots compare three different models across a benchmark set. These plots offer a clear visual summary of how closely each model approaches the best solution.

Performance plot comparing the objective values of different CVRP models on a benchmark set. The Miller–Tucker–Zemlin model performs best on most instances and remains close to the best on the rest. The other two models find the best solution in only about 10% of instances but solve roughly 70% within 2% of the best known solution, with multiple_circuit showing a slight advantage.

This can of course also be done for the lower bounds produced by each model.

Performance plot comparing the lower bounds produced by each CVRP model. The add_circuit model consistently achieves the best bounds, while the other two models yield bounds that are up to 20% worse in the best case and up to 100% worse (i.e., half the quality) on some instances.

# MIT License
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.axes import Axes


def plot_performance_profile(
    data: pd.DataFrame,
    instance_column: str,
    strategy_column: str,
    metric_column: str,
    direction: str,
    comparison: str = "relative",
    title: str | None = None,
    highlight_best: bool = False,
    ax: Axes | None = None,
    scale: str | None = None,
    log_base: int = 2,
    figsize: tuple = (9, 6),
) -> Axes:
    """
    Plot a performance profile, either on a relative-ratio basis or absolute-difference basis:
      - For comparison="relative":
          x-axis: performance ratio τ (log scale if τ_max > 10)
          τ = (value / best) if direction="min", or τ = (best / value) if direction="max".
      - For comparison="absolute":
          x-axis: absolute difference Δ = (value - best) if direction="min",
                                      or Δ = (best - value) if direction="max".
      - y-axis: proportion of problems with τ (or Δ) ≤ x for each solver.
      - If highlight_best=True, detect and bold the dominating solver curve (AUC in appropriate space).
      - Ensures a reasonable number of ticks on the x-axis.

    Args:
        data: DataFrame with columns [instance, strategy, metric].
        instance_column: column name identifying each problem instance.
        strategy_column: column name identifying each solver/strategy.
        metric_column: column name of the performance metric (e.g. runtime or cost).
        direction: "min" if lower metric → better, "max" if higher → better.
        comparison: "relative" or "absolute".
        title: Optional plot title.
        highlight_best: If True, find the solver with largest AUC and draw it in bold.
        ax: An existing matplotlib Axes to draw into. If None, a new Figure+Axes will be created using figsize.
        scale: x-axis scale override ("linear" or "log"); if None, chosen automatically.
        log_base: base for log scale if used (default 2).
        figsize: Tuple (width, height). Only used if ax is None.

    Returns:
        The matplotlib Axes containing the performance profile.
    """
    if direction not in ("min", "max"):
        raise ValueError("`direction` must be 'min' or 'max'.")
    if comparison not in ("relative", "absolute"):
        raise ValueError("`comparison` must be 'relative' or 'absolute'.")

    # 1) Compute best value per instance
    best_val = data.groupby(instance_column)[metric_column].agg(direction)

    # 2) Pivot to get per-instance × per-strategy medians
    pivot = (
        data.groupby([instance_column, strategy_column])[metric_column]
        .median()
        .unstack(fill_value=np.nan)
    )

    # 3) Build comparison matrix C[p, s]
    comp = pd.DataFrame(index=pivot.index, columns=pivot.columns, dtype=float)

    if comparison == "relative":
        for strat in pivot.columns:
            if direction == "min":
                comp[strat] = pivot[strat] / best_val
            else:  # direction == "max"
                comp[strat] = best_val / pivot[strat]
        comp = comp.replace([np.inf, -np.inf, 0.0], np.nan)

    else:  # comparison == "absolute"
        for strat in pivot.columns:
            if direction == "min":
                comp[strat] = pivot[strat] - best_val
            else:  # direction == "max"
                comp[strat] = best_val - pivot[strat]
        comp = comp.replace([np.inf, -np.inf], np.nan)

    # 4) Collect all distinct x-values (τ or Δ), including baseline
    all_vals = comp.values.flatten()
    finite_vals = all_vals[np.isfinite(all_vals)]
    baseline = 1.0 if comparison == "relative" else 0.0
    all_x = np.unique(np.sort(finite_vals))
    all_x = np.concatenate(([baseline], all_x))
    all_x = np.unique(np.sort(all_x))

    # 5) Build performance-profile DataFrame ρ(x)
    n_instances = comp.shape[0]
    profile = pd.DataFrame(index=all_x, columns=comp.columns, dtype=float)

    for x in all_x:
        leq = (comp <= x).sum(axis=0)
        profile.loc[x] = leq / n_instances

    # 6) Identify dominating solver if requested (max AUC)
    best_solver = None
    if highlight_best:
        if comparison == "relative":
            # integrate ρ(τ) w.r.t. log(τ)
            log_x = np.log(all_x)
            areas = {}
            for strat in profile.columns:
                y = profile[strat].astype(float).values
                areas[strat] = np.trapz(y, x=log_x)
            best_solver = max(areas, key=areas.get)
        else:
            # integrate ρ(Δ) w.r.t. Δ
            areas = {}
            for strat in profile.columns:
                y = profile[strat].astype(float).values
                areas[strat] = np.trapz(y, x=all_x)
            best_solver = max(areas, key=areas.get)

    # 7) Create or use existing Axes
    if ax is None:
        fig, ax = plt.subplots(figsize=figsize)
    else:
        fig = ax.figure

    # 8) Determine scale if not overridden
    if scale is None:
        if comparison == "relative" and all_x[-1] > 10:
            use_log = True
        else:
            use_log = False
    else:
        use_log = scale == "log"

    # 9) Plot each solver’s curve
    for strat in profile.columns:
        y = profile[strat].astype(float)
        if highlight_best and strat == best_solver:
            ax.step(all_x, y, where="post", label=strat, linewidth=3.0, alpha=1.0)
        else:
            ax.step(
                all_x,
                y,
                where="post",
                label=strat,
                linewidth=1.5,
                alpha=0.6 if highlight_best else 1.0,
            )

    # 10) Axis scaling and limits
    if comparison == "relative":
        if use_log:
            ax.set_xscale("log", base=log_base)
            ax.set_xlim(all_x[1], all_x[-1] * 1.1)
        else:
            ax.set_xscale("linear")
            ax.set_xlim(1.0, all_x[-1] * 1.1)
        xlabel = (
            f"Within this factor of the best (log{log_base} scale)"
            if use_log
            else "Within this factor of the best (linear scale)"
        )
    else:  # absolute
        ax.set_xscale("linear")
        ax.set_xlim(0.0, all_x[-1] * 1.1)
        xlabel = "Absolute difference from the best"

    ax.set_ylim(0.0, 1.02)
    ax.set_xlabel(xlabel, fontsize=12)
    ax.set_ylabel("Proportion of problems", fontsize=12)

    if title:
        ax.set_title(title, fontsize=14, pad=14)
    else:
        ax.set_title("Performance Profile", fontsize=14, pad=14)

    ax.axvline(x=baseline, color="gray", linestyle="--", alpha=0.7)
    ax.grid(True, which="both", linestyle=":", linewidth=0.5)

    # 11) Legend inside lower right
    ax.legend(loc="lower right", frameon=False)

    fig.tight_layout()
    return ax

Tangi Migot has written an excellent article on Performance Plots. Also take a look on the original paper Benchmarking optimization software with performance profiles (Dolan & Moré 2002)

Analyzing the Scalability of a Single Model

When working with a single model and aiming to analyze its scalability, a split plot can serve as an effective visualization. This type of plot shows the model’s runtime across instances of varying size, under a fixed time limit. If an instance is solved within the time limit, its actual runtime is shown. If not, the point is plotted above the time limit on a transformed y-axis that now displays the optimality gap instead of runtime.

An example of such a plot is shown below. Since aggregating this data into a line plot can be challenging, the visualization may become cluttered if too many instances are included or if multiple models are compared simultaneously.

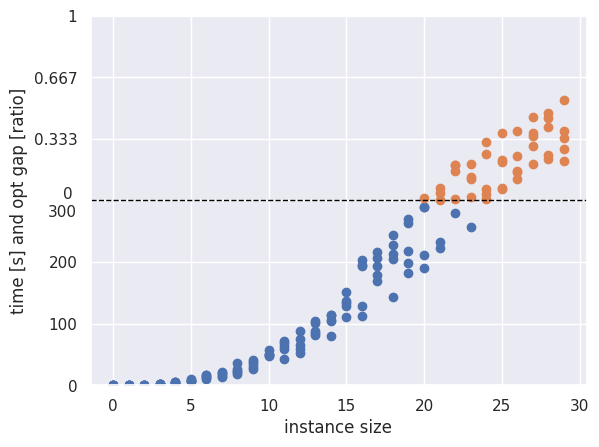Split plot illustrating runtime (for solved instances) and optimality gap (for unsolved instances). The y-axis is divided into two regions: one showing actual runtimes for instances solved within the time limit, and one showing optimality gaps for instances where the time limit was exceeded.

For many problems, there is no single instance size metric to compare over. Usually, you can still classify the instances into size categories. However, for especially complex problems, it may be best to just provide a table with the results for the largest instances to give an idea of the model's scalability.

Importance of Including Tables

Tables offer a concise and detailed view of benchmarking results. They allow readers to verify the accuracy of reported data, inspect individual instances, and complement high-level visual summaries such as plots.

While the previous sections presented insightful plots for visualizing performance trends, it is essential to also include at least one table that contains the raw results for the key benchmark instances. Many high-quality papers rely solely on tables to present their results, as they provide transparency and precision.

However, avoid including every table with all available data—this applies even to appendices. Instead, consider what information a critical reader would need to verify that your plots are not misleading. Focus on presenting the most relevant and interpretable results. A comprehensive dataset can always be linked in an external repository, but the tables within your paper should remain clear, selective, and to the point.

Example table from a recent publication, presenting detailed results of a new algorithm across benchmark instances. While less intuitive than plots, such tables enable readers to examine individual outcomes in detail.

Distinguishing Exploratory and Workhorse Studies in Benchmarking

Before diving into comprehensive benchmarking for scientific publications, it is essential to conduct preliminary investigations to assess your model’s capabilities and identify any foundational issues. This phase, known as exploratory studies, is crucial for establishing the basis for more detailed benchmarking, subsequently termed as workhorse studies. These latter studies aim to provide reliable answers to specific research questions and are often the core of academic publications. It is important to explicitly differentiate between these two study types and maintain their distinct purposes: exploratory studies for initial understanding and flexibility, and workhorse studies for rigorous, reproducible research.

For a comprehensive exploration of benchmarking, I highly recommend Catherine C. McGeoch's book, "A Guide to Experimental Algorithmics", which offers an in-depth discussion on this topic.

Exploratory Studies: Foundation Building

Exploratory studies serve as a first step toward understanding both your model and the problem it aims to solve. This phase is focused on building intuition and identifying key characteristics before committing to formal benchmarking.

• Objective: The goal at this stage is to gain early insights — not to draw definitive conclusions. Exploratory studies help identify realistic instance sizes, anticipate potential challenges, and narrow down hyperparameter search spaces.

Avoid setting up elaborate benchmarking frameworks during this phase. Keep the process lightweight and flexible to enable rapid iteration. If updating your benchmarks becomes cumbersome each time you adjust your model, it will slow your progress and — since benchmarking code tends to be tedious — you may lose motivation quickly.

From personal experience, I noticed a significant drop in productivity when I first learned to create robust benchmarking setups. I began treating even exploratory phases with the same level of rigor, which led to over-investing in decisions that did not yet warrant deep analysis. This approach forced me to get everything right too early and led to spending excessive time on unresolved details.

Instead, strike a balance: avoid letting things become disorganized, but postpone formal benchmarking until you're ready to share results. For example, I used quick exploratory studies in a single jupyter notebook to estimate appropriate instance sizes for the benchmark plots shown earlier.

Workhorse Studies: Conducting In-depth Evaluations

Workhorse studies follow the exploratory phase, characterized by more structured and meticulous approaches. This stage is vital for a comprehensive evaluation of your model and collecting substantive data for analysis.

• Objective: These studies are designed to answer specific research questions and provide meaningful insights. The approach here is more methodical, focusing on clearly defined research questions. The benchmarks designed should be well-structured and large enough to yield statistically significant results.

Remember, the aim is not to create a flawless benchmark right away but to evolve it as concrete questions emerge and as your understanding of the model and problem deepens. These studies, unlike exploratory ones, will be the focus of your scientific publications, with exploratory studies only referenced for justifying certain lesser design decisions.

Selecting a Robust Benchmark Instance Set

Choosing the right set of benchmark instances is a crucial step for effective evaluation of your models and solvers. The instance set forms the foundation of your experimental results and directly influences the insights you can draw.

Exploratory vs. Workhorse Studies

• In exploratory studies, the instance set can start small and simple, allowing you to quickly gain initial insights and identify potential issues.
• For workhorse studies — which aim for comprehensive, statistically sound evaluations — the instance set must be carefully curated to ensure representativeness and reliability.

Sources of Benchmark Instances

• Real-world instances are ideal because they reflect practical problem characteristics. However, such instances are often limited in number and may not cover the full range of problem difficulty or size needed for robust analysis.
• Established public benchmarks (e.g., TSPLIB for the Traveling Salesman Problem) provide a valuable basis for comparison with prior research. Yet, be mindful of their limitations such as uneven instance sizes or lack of heterogeneity, which can affect the generality of conclusions.

Generating Custom Instances

When real-world or public benchmarks are insufficient, generating your own instances is necessary. Aim to:

• Include enough instances in each size or difficulty category (for example, 10 instances per size class) to enable statistically meaningful results.
• Design instance generators that capture realistic features of the problem domain. For example, for TSP, random uniform points may not capture real-world clustering or alignment patterns common in urban layouts.
• Use diverse generation methods or sample from large existing instances to mimic realistic distributions.

Using Multiple Benchmark Sets

It is often beneficial to evaluate your models on two complementary sets:

1. A real-world or application-driven set—smaller but highly relevant.
2. A larger synthetic or randomized set—allowing detailed statistical analysis.

Keep these sets separate during analysis to avoid dominance of one data type and to demonstrate the robustness of your results across diverse scenarios.

Practical Considerations

• Separate instance creation from experiment execution. Generate and save benchmark instances independently to minimize errors and improve reproducibility.
• Be cautious with pseudo-random generators. Although deterministic in principle, their use can inadvertently introduce irreproducibility if seeds or environments are not carefully controlled.
• Share instances directly when possible, including both the pre-generated instances and the generation code. This ensures reproducibility and allows others to verify results without needing to regenerate instances, which may depend on specific environments or random seeds. This makes replication easier for others as it may still be relevant in twenty years, when your code may appear outdated to future generations of researchers, whereas quickly writing a parser can already today be done by AI.

An excellent example of a well-crafted benchmark is the MIPLIB collection, widely used in Mixed Integer Programming research to evaluate solvers like Gurobi and CPLEX.

To deepen your understanding of benchmark instance diversity, consider the concept of Instance Space Analysis. Kate Smith-Miles offers an insightful 30-minute talk on this topic, exploring how analyzing the space of instances can guide better instance selection and generation.

Efficiently Managing Your Benchmarks

Benchmark data management can quickly become complex, especially when juggling multiple experiments and research questions. The following strategies can help keep your workflow organized and your results reliable:

• Folder Structure: Maintain a clear and consistent folder hierarchy for your experiments. A typical setup uses a top-level evaluations directory with descriptive subfolders for each experiment. For example:

  evaluations
  ├── tsp
  │   ├── 2023-11-18_random_euclidean
  │   │   ├── PRIVATE_DATA
  │   │   │   ├── ... all data for debugging and internal use
  │   │   ├── PUBLIC_DATA
  │   │   │   ├── ... curated data intended for sharing
  │   │   ├── README.md            # Brief description of the experiment
  │   │   ├── 00_generate_instances.py
  │   │   ├── 01_run_experiments.py
  │   │   ├── ...
  │   ├── 2023-11-18_tsplib
  │   │   ├── PRIVATE_DATA
  │   │   │   ├── ... debugging data
  │   │   ├── PUBLIC_DATA
  │   │   │   ├── ... selected shareable data
  │   │   ├── README.md
  │   │   ├── 01_run_experiments.py
  │   │   ├── ...
  

• Documentation and Redundancy: Some redundancy in your data and code is acceptable if it aids understanding, but thorough documentation is essential. Clearly describe each experiment’s purpose, methodology, and results to facilitate future reference and reproducibility.

• Simplified Results for Easy Access: Keep a streamlined version of your results specifically for plotting and sharing. This makes it much easier to adapt figures and tables later—especially if you need to meet different formatting requirements for journals versus conferences. Without such preparation, reformatting old results can become a frustrating and time-consuming task.

• Comprehensive Data Storage: Save all data generated during experiments, even if it seems insignificant at the time. This ensures a complete record for later analysis, troubleshooting, or unexpected questions. Because raw data can be large, organize it into two separate folders: one containing all data for internal use, and another with a curated subset suitable for sharing.

• Experiment Flexibility: Design your experiments to be interruptible and extensible. This flexibility allows you to pause and resume long-running studies or add new solvers and configurations without re-running everything from scratch. This is particularly valuable for exploratory studies with frequent iterations and also for lengthy workhorse studies.

• Leveraging Technology: Use cluster management tools like Slurm to distribute your experiments efficiently across computing resources. Faster turnaround times accelerate your research progress and enable quicker decision-making.

Because existing tools didn’t fully meet my needs, I developed AlgBench to manage benchmarking results and Slurminade to simplify experiment distribution on clusters via a decorator interface. However, there may now be better solutions available, especially from the machine learning community. If you know of tools you like, please drop me a line — I would be happy to explore them.

The CP-SAT Primer is authored by Dominik Krupke at TU Braunschweig, Algorithms Division. It is licensed under the CC-BY-4.0 license.

The primer is written for educational purposes and may be incomplete or incorrect in places. If you find this primer helpful, please star the GitHub repository, to let me know with a single click that it has made an impact. As an academic, I also enjoy hearing about how you use CP-SAT to solve real-world problems.