Understanding the CP-SAT Log

If you want to master CP-SAT, understanding the log is crucial. The log is the output of the solver that shows you what the solver is doing and how it is progressing.
The log consists of different parts. Let us go through them step by step.
 Use the Log Analyzer to get your
own logs explained to you.
|
As a reminder, you activate logging with
solver.parameters.log_search_progress = True # Enable logging
Initialization
The log starts with the version of CP-SAT, the parameters you set, and how many
workers it has been using. For example, we have set a time limit via
max_time_in_seconds to 30 seconds. If you are given a log, you can directly
see under which conditions the solver was running.
Starting CP-SAT solver v9.10.4067
Parameters: max_time_in_seconds: 30 log_search_progress: true relative_gap_limit: 0.01
Setting number of workers to 16
Initial Model Description
The next block provides an overview of the model before presolve, detailing the number of variables and constraints, as well as their coefficients and domains.
Initial optimization model '': (model_fingerprint: 0x1d316fc2ae4c02b1)
#Variables: 450 (#bools: 276 #ints: 6 in objective)
- 342 Booleans in [0,1]
- 12 in [0][10][20][30][40][50][60][70][80][90][100]
- 6 in [0][10][20][30][40][100]
- 6 in [0][80][100]
- 6 in [0][100]
- 6 in [0,1][34][67][100]
- 12 in [0,6]
- 18 in [0,7]
- 6 in [0,35]
- 6 in [0,36]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kBoolOr: 30 (#literals: 72)
#kLinear1: 33 (#enforced: 12)
#kLinear2: 1'811
#kLinear3: 36
#kLinearN: 94 (#terms: 1'392)
For example, - 12 in [22,57] indicates that there are 12 variables with a
domain of [22,57], meaning their values can range between 22 and 57.
Similarly, #kLinearN: 94 (#terms: 1'392) indicates the presence of 94 linear
constraints with 1,392 coefficients.
Comparing this data to the model after presolve (coming up soon) is useful to ensure it aligns with your expectations. The presolve phase often reformulates your model extensively to enhance efficiency.
Since most optimization models are created dynamically in code, reviewing this section can help identify bugs or inefficiencies. Take the time to verify that the numbers match your expectations and ensure you do not have too many or too few variables or constraints of a certain type. This step is crucial as it also provides insight into the number of auxiliary variables in your model, helping you better understand its structure and complexity.
Presolve Log
The next block represents the presolve phase, an essential component of CP-SAT.
During this phase, the solver reformulates your model for greater efficiency.
For instance, it may detect an affine relationship between variables, such as
x=2y-1, and replace x with 2y-1 in all constraints. It can also identify
and remove redundant constraints or unnecessary variables. For example, the log
entry rule 'presolve: 33 unused variables removed.' was applied 1 time may
indicate that some variables created by your code were unnecessary or became
redundant due to the reformulation. Multiple rounds of applying various rules
for domain reduction, expansion, equivalence checking, substitution, and probing
are performed during presolve. These rules can significantly enhance the
efficiency of your model, though they may take some time to run. However, this
time investment usually pays off during the search phase.
Starting presolve at 0.00s
3.26e-04s 0.00e+00d [DetectDominanceRelations]
6.60e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=4 #num_dual_strengthening=3
2.69e-05s 0.00e+00d [ExtractEncodingFromLinear] #potential_supersets=44 #potential_subsets=12
[Symmetry] Graph for symmetry has 2'224 nodes and 5'046 arcs.
[Symmetry] Symmetry computation done. time: 0.000374304 dtime: 0.00068988
[Symmetry] #generators: 2, average support size: 12
[Symmetry] 12 orbits with sizes: 2,2,2,2,2,2,2,2,2,2,...
[Symmetry] Found orbitope of size 6 x 2
[SAT presolve] num removable Booleans: 0 / 309
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [3.0778e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [4.6758e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
1.10e-02s 9.68e-03d [Probe] #probed=1'738 #new_bounds=12 #new_binary_clauses=1'111
2.34e-03s 0.00e+00d [MaxClique] Merged 602(1374 literals) into 506(1960 literals) at_most_ones.
3.31e-04s 0.00e+00d [DetectDominanceRelations]
1.89e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=1
5.45e-04s 0.00e+00d [ProcessAtMostOneAndLinear]
8.19e-04s 0.00e+00d [DetectDuplicateConstraints] #without_enforcements=306
8.62e-05s 7.21e-06d [DetectDominatedLinearConstraints] #relevant_constraints=114 #num_inclusions=42
...
Presolve summary:
- 54 affine relations were detected.
- rule 'TODO dual: make linear1 equiv' was applied 6 times.
- rule 'TODO dual: only one blocking constraint?' was applied 1'074 times.
- rule 'TODO dual: only one unspecified blocking constraint?' was applied 48 times.
- rule 'TODO duplicate: identical constraint with different enforcements' was applied 612 times.
- rule 'TODO linear2: contains a Boolean.' was applied 1'626 times.
- rule 'TODO symmetry: add symmetry breaking inequalities?' was applied 2 times.
...
- rule 'objective: variable not used elsewhere' was applied 15 times.
- rule 'presolve: 33 unused variables removed.' was applied 1 time.
- rule 'presolve: iteration' was applied 2 times.
- rule 'variables with 2 values: create encoding literal' was applied 12 times.
- rule 'variables with 2 values: new affine relation' was applied 12 times.
- rule 'variables: canonicalize affine domain' was applied 30 times.
- rule 'variables: detect half reified value encoding' was applied 54 times.
The presolve log can be challenging to read, but it provides vital information on the simplifications and optimizations made by CP-SAT. Reviewing this log can help you understand the transformations applied to your model, allowing you to identify and address any unnecessary variables or constraints in your code.
Presolved Model
This is the most important block of the presolve phase and gives an overview of the model after presolve. It contains the number of variables and constraints, as well as coefficients and domains.
- 200 in [0,199] will indicate that there are 200 variables with domain
[0,199], i.e., values between 0 and 199. - 6 in [0,1][34][67][100] will
indicate that there are 6 variables with domain [0,1][34][67][100], i.e.,
values 0, 1, 34, 67, and 100. #kLinearN: 3'000 (#terms: 980'948) indicates
that there are 3000 linear constraints with 980’948 coefficients.
It is useful to compare this to the initial model, to see if your model was simplified by presolve, which indicates that you can simplify your model yourself, saving presolve time. If you notice that a lot of time is spent in presolve but it does not simplify your model, you can try to disable/reduce presolve.
It is also interesting to see if the presolve replaced some of your constraints with more efficient ones.
Presolved optimization model '': (model_fingerprint: 0xb4e599720afb8c14)
#Variables: 405 (#bools: 261 #ints: 6 in objective)
- 309 Booleans in [0,1]
- 12 in [0][2,6]
- 6 in [0][4,5]
- 6 in [0,3]
- 6 in [0,4]
- 6 in [0,6]
- 6 in [0,7]
- 12 in [0,10]
- 12 in [0,13]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kAtMostOne: 452 (#literals: 1'750)
#kBoolAnd: 36 (#enforced: 36) (#literals: 90)
#kBoolOr: 12 (#literals: 36)
#kLinear1: 854 (#enforced: 854)
#kLinear2: 42
#kLinear3: 24
#kLinearN: 48 (#enforced: 18) (#terms: 1'046)
 This is the same model as in the initial model description. Take some time to compare the two and see how much the presolve-phase has reformulated the model. |
Preloading Model
This block serves as a prelude to the search phase and provides an overview of the model at the beginning of the search. Typically, this information is not very interesting unless the presolve phase was highly effective, essentially solving the model before the search phase begins. This can lead to entries that look very similar to that of the actual search phase, which comes next.
Preloading model.
#Bound 0.05s best:-inf next:[-0.7125] initial_domain
[Symmetry] Graph for symmetry has 2,111 nodes and 5,096 arcs.
[Symmetry] Symmetry computation done. time: 0.000365377 dtime: 0.00068122
[Symmetry] #generators: 2, average support size: 12
[Symmetry] Found orbitope of size 6 x 2
#Model 0.05s var:405/405 constraints:1468/1468
Search Phase
The search progress log is an essential element of the overall log, crucial for identifying performance bottlenecks. It clearly demonstrates the solver’s progression over time and pinpoints where it faces significant challenges. It is important to discern whether the upper or lower bounds are causing issues, or if the solver initially finds a near-optimal solution but struggles to minimize a small remaining gap.
 For models without an objective, especially the log of the search phase will look very different. This chapter focuses on models with an objective. |
The structure of the log entries is standardized as follows:
EVENT NAME | TIME | BEST SOLUTION | RANGE OF THE SEARCH | COMMENT
For instance, an event marked #2 indicates the discovery of the second
solution. Here, you will observe an improvement in the BEST SOLUTION metric. A
notation like best:16 confirms that the solver has found a solution with a
value of 16.
An event with #Bound denotes an enhancement in the bound, as seen by a
reduction in the RANGE OF THE SEARCH. A detail such as next:[7,14] signifies
that the solver is now focused on finding a solution valued between 7 and 14.
The COMMENT section provides essential information about the strategies that
led to these improvements.
Events labeled #Model signal modifications to the model, such as fixing
certain variables.
Starting search at 0.05s with 16 workers.
11 full problem subsolvers: [core, default_lp, lb_tree_search, max_lp, no_lp, objective_lb_search, probing, pseudo_costs, quick_restart, quick_restart_no_lp, reduced_costs]
4 first solution subsolvers: [fj_long_default, fj_short_default, fs_random, fs_random_quick_restart]
9 incomplete subsolvers: [feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, rins/rens, rnd_cst_lns, rnd_var_lns, violation_ls]
3 helper subsolvers: [neighborhood_helper, synchronization_agent, update_gap_integral]
#1 0.06s best:-0 next:[1,7125] fj_short_default(batch:1 #lin_moves:0 #lin_evals:0 #weight_updates:0)
#2 0.07s best:1050 next:[1051,7125] fj_long_default(batch:1 #lin_moves:1'471 #lin_evals:2'102 #weight_updates:123)
#3 0.08s best:1051 next:[1052,7125] quick_restart_no_lp (fixed_bools=0/884)
#Bound 0.09s best:1051 next:[1052,1650] default_lp
#4 0.10s best:1052 next:[1053,1650] quick_restart_no_lp (fixed_bools=22/898)
#5 0.10s best:1053 next:[1054,1650] quick_restart_no_lp (fixed_bools=22/901)
#6 0.11s best:1055 next:[1056,1650] quick_restart_no_lp (fixed_bools=22/906)
#7 0.11s best:1056 next:[1057,1650] quick_restart_no_lp (fixed_bools=22/909)
#8 0.11s best:1057 next:[1058,1650] quick_restart_no_lp (fixed_bools=22/913)
#9 0.11s best:1058 next:[1059,1650] quick_restart_no_lp (fixed_bools=22/914)
#10 0.12s best:1059 next:[1060,1650] quick_restart_no_lp (fixed_bools=26/916)
#11 0.12s best:1060 next:[1061,1650] quick_restart_no_lp (fixed_bools=26/917)
#12 0.12s best:1061 next:[1062,1650] quick_restart_no_lp (fixed_bools=26/918)
#13 0.13s best:1062 next:[1063,1650] quick_restart_no_lp (fixed_bools=28/918)
#14 0.13s best:1063 next:[1064,1650] quick_restart_no_lp (fixed_bools=28/921)
#Bound 0.13s best:1063 next:[1064,1579] lb_tree_search
#15 0.13s best:1064 next:[1065,1579] quick_restart_no_lp (fixed_bools=28/924)
#Model 0.13s var:404/405 constraints:1435/1468
#16 0.13s best:1065 next:[1066,1579] quick_restart_no_lp (fixed_bools=28/930)
#17 0.13s best:1066 next:[1067,1579] quick_restart_no_lp (fixed_bools=28/932)
#18 0.14s best:1067 next:[1068,1579] quick_restart_no_lp (fixed_bools=28/935)
#19 0.14s best:1071 next:[1072,1579] quick_restart_no_lp (fixed_bools=28/946)
#20 0.15s best:1072 next:[1073,1579] quick_restart_no_lp (fixed_bools=28/950)
#21 0.15s best:1089 next:[1090,1579] quick_restart_no_lp (fixed_bools=28/966)
#22 0.15s best:1090 next:[1091,1579] quick_restart_no_lp (fixed_bools=28/966)
...
#Bound 8.73s best:1449 next:[1450,1528] lb_tree_search (nodes=13/18 rc=0 decisions=133 @root=28 restarts=0)
#Model 8.99s var:390/405 constraints:1292/1468
#Bound 9.37s best:1449 next:[1450,1527] lb_tree_search (nodes=15/20 rc=0 decisions=152 @root=28 restarts=0)
#Bound 11.79s best:1449 next:[1450,1526] lb_tree_search (nodes=78/83 rc=0 decisions=327 @root=28 restarts=0)
#Bound 12.40s best:1449 next:[1450,1525] lb_tree_search (nodes=96/104 rc=0 decisions=445 @root=28 restarts=0)
#Bound 13.50s best:1449 next:[1450,1524] lb_tree_search (nodes=123/138 rc=0 decisions=624 @root=28 restarts=0)
#Bound 15.71s best:1449 next:[1450,1523] lb_tree_search (nodes=164/180 rc=0 decisions=847 @root=29 restarts=0)
#132 16.69s best:1450 next:[1451,1523] rnd_var_lns (d=0.88 s=657 t=0.10 p=0.54 stall=53 h=folio_rnd)
#Bound 17.13s best:1450 next:[1451,1522] lb_tree_search (nodes=176/192 rc=0 decisions=1001 @root=30 restarts=0)
#Model 17.85s var:389/405 constraints:1289/1468
#Bound 19.35s best:1450 next:[1451,1521] lb_tree_search (nodes=44/44 rc=0 decisions=1112 @root=33 restarts=1)
#Bound 20.12s best:1450 next:[1451,1520] lb_tree_search (nodes=53/53 rc=0 decisions=1176 @root=34 restarts=1)
#Bound 22.08s best:1450 next:[1451,1519] lb_tree_search (nodes=114/114 rc=0 decisions=1369 @root=35 restarts=1)
#Bound 23.92s best:1450 next:[1451,1518] lb_tree_search (nodes=131/131 rc=0 decisions=1517 @root=36 restarts=1)
#Bound 25.84s best:1450 next:[1451,1517] lb_tree_search (nodes=174/174 rc=0 decisions=1754 @root=36 restarts=1)
#Bound 29.35s best:1450 next:[1451,1515] objective_lb_search
As this log is event-driven, it can be challenging to interpret. The Log Analyzer helps by automatically plotting these values in a more understandable way. Since the values at the beginning of the search are often out of scale, use the zoom function to focus on the relevant parts of the search.
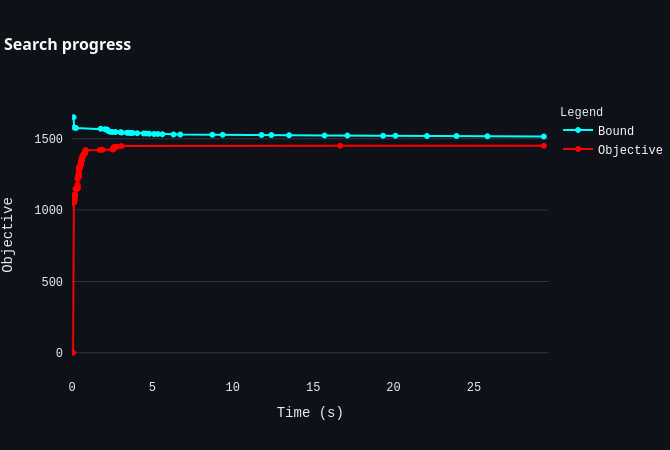 | 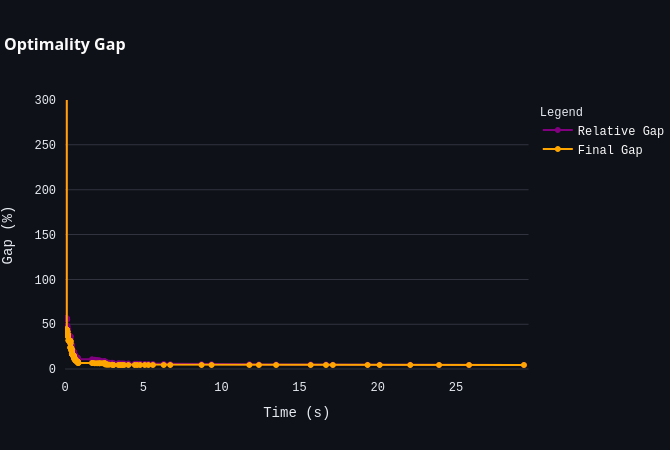 | 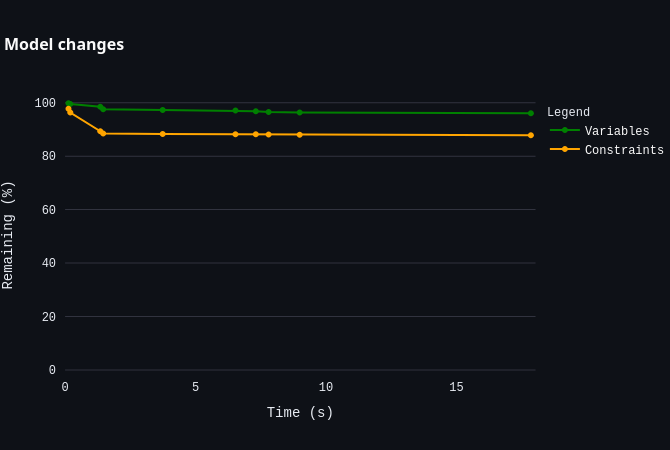 |
|---|---|---|
| Shows how the lower and upper bounds change over time. | Shows how quickly the optimality gap converges. | Shows how the model changes over time as new insights from the search allow the solver to fix variables. |
Subsolver Details
Now there comes a lot of information about the different subsolvers that are used. This is a very detailed part of the log and can be overwhelming. You already need to be rather deep into the details of CP-SAT to actually make any use of this information. It is primarily intended for the developers of CP-SAT. It gives you insights into how the various subsolvers have been contributing to the solution, how the otherwise hidden LP-techniques, including cutting planes, have been used, and how the different heuristics have been applied. Based on this data, you could try to tune the various parameters of CP-SAT for your problem. However, note that you will probably need a lot of experience and experiments to gain an advantage compared to the default settings.
Task timing n [ min, max] avg dev time n [ min, max] avg dev dtime
'core': 1 [ 29.95s, 29.95s] 29.95s 0.00ns 29.95s 1 [ 27.99s, 27.99s] 27.99s 0.00ns 27.99s
'default_lp': 1 [ 29.94s, 29.94s] 29.94s 0.00ns 29.94s 1 [ 21.11s, 21.11s] 21.11s 0.00ns 21.11s
'feasibility_pump': 123 [ 4.51ms, 70.61ms] 38.93ms 9.87ms 4.79s 122 [ 6.31ms, 41.77ms] 17.96ms 6.53ms 2.19s
'fj_long_default': 1 [ 10.28ms, 10.28ms] 10.28ms 0.00ns 10.28ms 1 [ 2.08ms, 2.08ms] 2.08ms 0.00ns 2.08ms
'fj_short_default': 1 [579.83us, 579.83us] 579.83us 0.00ns 579.83us 0 [ 0.00ns, 0.00ns] 0.00ns 0.00ns 0.00ns
'fs_random': 1 [ 6.57ms, 6.57ms] 6.57ms 0.00ns 6.57ms 1 [ 20.00ns, 20.00ns] 20.00ns 0.00ns 20.00ns
'fs_random_quick_restart': 1 [ 6.82ms, 6.82ms] 6.82ms 0.00ns 6.82ms 1 [ 20.00ns, 20.00ns] 20.00ns 0.00ns 20.00ns
'graph_arc_lns': 123 [ 3.65ms, 430.55ms] 169.44ms 106.16ms 20.84s 123 [ 10.00ns, 119.31ms] 61.95ms 43.70ms 7.62s
...
Clauses shared Num
'core': 137
'default_lp': 1
'lb_tree_search': 4
'max_lp': 1
'no_lp': 10
'objective_lb_search': 3
'pseudo_costs': 4
'quick_restart': 4
'quick_restart_no_lp': 74
'reduced_costs': 2
Summary
This final block of the log contains a summary by the solver. Here you find the most important information, such as how successful the search was.
You can find the original documentation here.
CpSolverResponse summary:
status: FEASIBLE # The status of the search. Can be FEASIBLE, OPTIMAL, INFEASIBLE, UNKNOWN, or MODEL_INVALID.
objective: 1450 # The value of the objective function for the best solution found.
best_bound: 1515 # The proven bound on the objective function, i.e., the best possible value.
integers: 416
booleans: 857
conflicts: 0
branches: 370
propagations: 13193
integer_propagations: 6897
restarts: 370
lp_iterations: 0
walltime: 30.4515 # The time in seconds since solver creation.
usertime: 30.4515
deterministic_time: 306.548
gap_integral: 1292.47 # The integral of the gap over time. A lower value will indicate that the solver is converging faster.
solution_fingerprint: 0xf10c47f1901c2c16 # Useful to check if two runs result in the same solution.
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (680⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.

