Parameters

The CP-SAT solver offers numerous parameters to control its behavior. These
parameters are implemented via
Protocol Buffers and can be
manipulated using the parameters member. To explore all available options,
refer to the well-documented proto file in the
official repository.
Below, I will highlight the most important parameters so you can get the most
out of CP-SAT.
 Only a few parameters, such as |
Logging
The log_search_progress parameter is crucial at the beginning. It enables
logging of the search progress, providing insights into how CP-SAT solves your
problem. While you may deactivate it later for production, it is beneficial
during development to understand the process and respond to any issues.
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
# Custom log function, for example, using the Python logging module instead of stdout
# Useful in a Jupyter notebook, where logging to stdout might not be visible
solver.log_callback = print # (str)->None
# If using a custom log function, you can disable logging to stdout
solver.parameters.log_to_stdout = False
The log offers valuable information for understanding CP-SAT and your optimization problem. It details aspects such as how many variables were directly removed and which techniques most effectively contributed to improving lower and upper bounds.
An example log might look like this:
Starting CP-SAT solver v9.10.4067
Parameters: max_time_in_seconds: 30 log_search_progress: true relative_gap_limit: 0.01
Setting number of workers to 16
Initial optimization model '': (model_fingerprint: 0x1d316fc2ae4c02b1)
#Variables: 450 (#bools: 276 #ints: 6 in objective)
- 342 Booleans in [0,1]
- 12 in [0][10][20][30][40][50][60][70][80][90][100]
- 6 in [0][10][20][30][40][100]
- 6 in [0][80][100]
- 6 in [0][100]
- 6 in [0,1][34][67][100]
- 12 in [0,6]
- 18 in [0,7]
- 6 in [0,35]
- 6 in [0,36]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kBoolOr: 30 (#literals: 72)
#kLinear1: 33 (#enforced: 12)
#kLinear2: 1'811
#kLinear3: 36
#kLinearN: 94 (#terms: 1'392)
Starting presolve at 0.00s
3.26e-04s 0.00e+00d [DetectDominanceRelations]
6.60e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=4 #num_dual_strengthening=3
2.69e-05s 0.00e+00d [ExtractEncodingFromLinear] #potential_supersets=44 #potential_subsets=12
[Symmetry] Graph for symmetry has 2'224 nodes and 5'046 arcs.
[Symmetry] Symmetry computation done. time: 0.000374304 dtime: 0.00068988
[Symmetry] #generators: 2, average support size: 12
[Symmetry] 12 orbits with sizes: 2,2,2,2,2,2,2,2,2,2,...
[Symmetry] Found orbitope of size 6 x 2
[SAT presolve] num removable Booleans: 0 / 309
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [3.0778e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [4.6758e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
1.10e-02s 9.68e-03d [Probe] #probed=1'738 #new_bounds=12 #new_binary_clauses=1'111
2.34e-03s 0.00e+00d [MaxClique] Merged 602(1374 literals) into 506(1960 literals) at_most_ones.
3.31e-04s 0.00e+00d [DetectDominanceRelations]
1.89e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=1
5.45e-04s 0.00e+00d [ProcessAtMostOneAndLinear]
8.19e-04s 0.00e+00d [DetectDuplicateConstraints] #without_enforcements=306
8.62e-05s 7.21e-06d [DetectDominatedLinearConstraints] #relevant_constraints=114 #num_inclusions=42
1.94e-05s 0.00e+00d [DetectDifferentVariables]
1.90e-04s 8.39e-06d [ProcessSetPPC] #relevant_constraints=560 #num_inclusions=24
2.01e-05s 0.00e+00d [FindAlmostIdenticalLinearConstraints]
...
Given the complexity of the log, I developed a tool to visualize and comment on it. You can copy and paste your log into the tool, which will automatically highlight the most important details. Be sure to check out the examples.
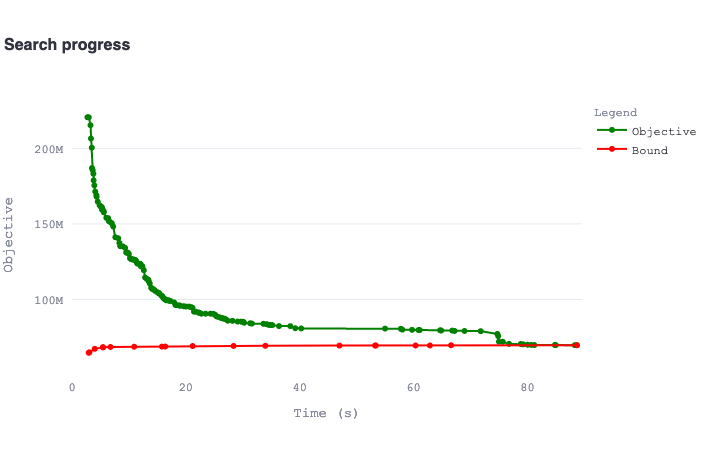 |
|---|
| A plot of the search progress over time as visualized by the log analyzer using information from the log (a different log than displayed above). This plot helps you understand which part of your problem is more challenging: finding a good solution or proving its quality. Based on this, you can implement appropriate countermeasures. |
We will revisit the logs in the next chapter.
 From my experience as a lecturer, I often encounter students who believe CP-SAT is stuck, only to discover that their model building includes an unnecessarily complex \( O(n^5) \) nested loop, which would take days to run. It is natural to assume that the issue lies with CP-SAT because it handles the hard part of solving the problem. However, even the seemingly simple part of model building can consume a lot of time if implemented incorrectly. By enabling logging, students could immediately see that the issue lies in their own code rather than with CP-SAT. This simple step can save a lot of time and frustration. |
Time Limit and Status
When working with large or complex models, the CP-SAT solver may not always reach an optimal solution within a reasonable time frame and could potentially run indefinitely. Therefore, setting a time limit is advisable, particularly in a production environment, to prevent the solver from running endlessly. Even within a time limit, CP-SAT often finds a reasonably good solution, although it may not be proven optimal.
Determining an appropriate time limit depends on various factors and usually requires some experimentation. I typically start with a time limit between 60 and 300 seconds, as this provides a balance between not having to wait too long during model testing and giving the solver enough time to find a good solution.
To set a time limit (in seconds) before running the solver, use the following command:
solver.parameters.max_time_in_seconds = 60 # 60s time limit
After running the solver, it is important to check the status to determine whether an optimal solution, a feasible solution, or no solution at all has been found:
status = solver.solve(model)
if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
print("We have a solution.")
else:
print("Help?! No solution available! :( ")
The possible status codes are:
OPTIMAL(4): An optimal solution has been found.FEASIBLE(2): A feasible solution has been found, and a bound may be available to assess its quality viasolver.best_objective_bound.INFEASIBLE(3): No solution can satisfy all constraints.MODEL_INVALID(1): The CP-SAT model is incorrectly specified.UNKNOWN(0): No solution was found, and no infeasibility proof is available. A bound may still be available.
To get the name from the status code, use solver.status_name(status).
In addition to limiting runtime, you can specify acceptable solution quality
using absolute_gap_limit and relative_gap_limit. The absolute limit stops
the solver when the solution is within a specified value of the bound. The
relative limit stops the solver when the objective value (O) is within a
specified ratio of the bound (B). To stop when the solution is (provably) within
5% of the optimum, use:
solver.parameters.relative_gap_limit = 0.05
For cases where progress stalls or for other reasons, solution callbacks can be used to halt the solver. With these, you can decide on every new solution if the solution is good enough or if the solver should continue searching for a better one. Unlike Gurobi, CP-SAT does not support adding lazy constraints from these callbacks (or at all), which is a significant limitation for problems requiring dynamic model adjustments.
To add a solution callback, inherit from the base class
CpSolverSolutionCallback. Documentation for this base class and its operations
is available
here.
class MySolutionCallback(cp_model.CpSolverSolutionCallback):
def __init__(self, data):
cp_model.CpSolverSolutionCallback.__init__(self)
self.data = data # Store data in the callback.
def on_solution_callback(self):
obj = self.objective_value # Best solution value
bound = self.best_objective_bound # Best bound
print(f"The current value of x is {self.Value(x)}")
if abs(obj - bound) < 10:
self.StopSearch() # Stop search for a better solution
# ...
solver.solve(model, MySolutionCallback(None))
An official example using callbacks is available.
 Bounds in optimization can be a double-edged sword. On one hand, they indicate how close you are to the optimal solution within your chosen model, and they allow you to terminate the optimization process early if the solution is sufficiently close. On the other hand, they can be misleading for two key reasons. First, the bounds pertain to the optimization model and may give a false sense of quality, as neither the model nor the data are typically perfect. Second, in some cases, obtaining good bounds within a reasonable time may be impossible, yet the solution might still be good—you simply may not realize it. This can lead to wasted resources as you pursue tighter models or better approaches with little to no real benefit. While bounds are extremely useful, it is important to understand their origin and limitations, and not regard them as the final determinant of solution quality. |
Besides querying the objective value of the best solution and the best known
bound, you can also access internal metrics such as self.num_booleans,
self.num_branches, and self.num_conflicts. These metrics will be discussed
later.
As of version 9.10, CP-SAT also supports bound callbacks, which are triggered when the proven bound improves. Unlike solution callbacks, which activate upon finding new solutions, bound callbacks are useful for stopping the search when the bound is sufficiently good. The syntax for bound callbacks differs from that of solution callbacks, as they are implemented as free functions that directly access the solver object.
solver = cp_model.CpSolver()
def bound_callback(bound):
print(f"New bound: {bound}")
if bound > 100:
solver.stop_search()
solver.best_bound_callback = bound_callback
Instead of using a simple function, you can also use a callable object to store a reference to the solver object. This approach allows you to define the callback outside the local scope, providing greater flexibility.
class BoundCallback:
def __init__(self, solver) -> None:
self.solver = solver
def __call__(self, bound):
print(f"New bound: {bound}")
if bound > 200:
print("Abort search due to bound")
self.solver.stop_search()
This method is more flexible than the solution callback and can be considered more Pythonic.
Additionally, whenever there is a new solution or bound, a log message is generated. You can hook into the log output to decide when to stop the search using CP-SAT’s log callback.
solver.parameters.log_search_progress = True # Enable logging
solver.log_callback = lambda msg: print("LOG:", msg) # (str) -> None
 Be careful when using callbacks, as they can slow down the solver significantly. Callbacks are often called frequently, forcing a switch back to the slower Python layer. I have often seen students frustrated by slow solver performance, only to discover that most of the solver’s time is spent in the callback function. Even if the operations within the callback are not complex, the time spent can add up quickly and affect overall performance. |
Parallelization
CP-SAT is a portfolio-solver that uses different techniques to solve the problem. There is some information exchange between the different workers, but it does not split the solution space into different parts, thus, it does not parallelize the branch-and-bound algorithm as MIP-solvers do. This can lead to some redundancy in the search, but running different techniques in parallel will also increase the chance of running the right technique. Predicting which technique will be the best for a specific problem is often hard, thus, this parallelization can be quite useful.
By default, CP-SAT leverages all available cores (including hyperthreading). You can control the parallelization of CP-SAT by setting the number of search workers.
solver.parameters.num_workers = 8 # use 8 cores
 For many models, you can boost performance by manually reducing the number of workers to match the number of physical cores, or even fewer. This can be beneficial for several reasons: it allows the remaining workers to run at a higher frequency, provides more memory bandwidth, and reduces potential interference between workers. However, be aware that reducing the number of workers might also decrease the overall chance of one of them making progress, as there are fewer directions being explored simultaneously. |
Here are the solvers used by CP-SAT 9.9 on different parallelization levels for an optimization problem and no additional specifications (e.g., decision strategies). Each row describes the addition of various solvers with respect to the previous row. Note that some parameters/constraints/objectives can change the parallelization strategy. Also check the official documentation.
| # Workers | Full Problem Subsolvers | First Solution Subsolvers | Incomplete Subsolvers | Helper Subsolvers |
|---|---|---|---|---|
| 1 | default_lp | No solver | No solver | No solver |
| 2 | +13 solvers: feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, packing_precedences_lns, packing_rectangles_lns, packing_slice_lns, rins/rens, rnd_cst_lns, rnd_var_lns, scheduling_precedences_lns, violation_ls | +3 solvers: neighborhood_helper, synchronization_agent, update_gap_integral | ||
| 3 | +1 solver: no_lp | |||
| 4 | +1 solver: max_lp | |||
| 5 | +1 solver: fj_short_default | |||
| 6 | +1 solver: quick_restart | |||
| 7 | +1 solver: reduced_costs | |||
| 8 | +1 solver: quick_restart_no_lp | |||
| 12 | +2 solvers: lb_tree_search, pseudo_costs | +2 solvers: fj_long_default, fs_random | ||
| 16 | +3 solvers: objective_lb_search, objective_shaving_search_no_lp, probing | +1 solver: fs_random_quick_restart | ||
| 20 | +2 solvers: objective_shaving_search_max_lp, probing_max_lp | +1 solver: fj_short_lin_default | ||
| 32 | +2 solvers: objective_lb_search_max_lp, objective_lb_search_no_lp | +8 solvers: fj_long_lin_default, fj_long_lin_random, fj_long_random, fj_short_lin_random, fj_short_random, fs_random_no_lp, fs_random_quick_restart_no_lp | +1 solver: violation_ls(3) | |
| 64 | +11 solvers: fj_long_default(2), fj_long_lin_default(2), fj_long_lin_random(2), fj_long_random(2), fj_short_default(2), fj_short_lin_default(2), fj_short_random(2), fs_random(6), fs_random_no_lp(6), fs_random_quick_restart(6), fs_random_quick_restart_no_lp(5) | +1 solver: violation_ls(7) |
Important steps:
- With a single worker, only the default subsolver is used.
- With two workers or more, CP-SAT starts using incomplete subsolvers, i.e., heuristics such as LNS.
- With five workers, CP-SAT will also have a first solution subsolver.
- With 32 workers, all 15 full problem subsolvers are used.
- For more than 32 workers, primarily the number of first solution subsolvers is increased.
Full problem subsolvers are solvers that search the full problem space, e.g., by a branch-and-bound algorithm. Available full problem subsolvers are:
default_lp: LCG-based search with default linearization of the model.max_lp: Same asdefault_lpbut with maximal linearization.no_lp: Same asdefault_lpbut without linearization.
lb_tree_search: This solver is focussed on improving the proven bound, not on finding better solutions. By disproving the feasibility of the cheapest nodes in the search tree, it incrementally improves the bound, but has only little chances to find better solutions.objective_lb_search: Also focussed on improving the bound by disproving the feasibility of the current lower bound.objective_lb_search_max_lp: With maximal linearization.objective_lb_search_no_lp: Without linearization.objective_shaving_search_max_lp: Should be quite similar toobjective_lb_search_max_lp.objective_shaving_search_no_lp: Should be quite similar toobjective_lb_search_no_lp.
probing: Fixing variables and seeing what happens.probing_max_lp: Same as probing but with maximal linearization.
pseudo_costs: Uses pseudo costs for branching, which are computed from historical changes in objective bounds following certain branching decisions.quick_restart: Restarts the search more eagerly. Restarts rebuild the search tree from scratch, but keep learned clauses. This allows to recover from bad decisions, and lead to smaller search trees by learning from the mistakes of the past.quick_restart_no_lp: Same asquick_restartbut without linearization.
reduced_costs: Uses the reduced costs of the linear relaxation for branching.core: A strategy from the SAT-community that extracts unsatisfiable cores of the formula.fixed: User-specified search strategy.
You can modify the used subsolvers by solver.parameters.subsolvers,
solver.parameters.extra_subsolvers, and solver.parameters.ignore_subsolvers.
This can be interesting, e.g., if you are using CP-SAT especially because the
linear relaxation is not useful (and the BnB-algorithm performing badly). There
are even more options, but for these you can simply look into the
documentation.
Be aware that fine-tuning such a solver is not a simple task, and often you do
more harm than good by tinkering around. However, I noticed that decreasing the
number of search workers can actually improve the runtime for some problems.
This indicates that at least selecting the right subsolvers that are best fitted
for your problem can be worth a shot. For example max_lp is probably a waste
of resources if you know that your model has a terrible linear relaxation. In
this context I want to recommend having a look on some relaxed solutions when
dealing with difficult problems to get a better understanding of which parts a
solver may struggle with (use a linear programming solver, like Gurobi, for
this).
You can evaluate the performance of the different strategies by looking at the
Solutions and Objective bounds blocks in the log. Here an example:
Solutions (7) Num Rank
'no_lp': 3 [1,7]
'quick_restart': 1 [3,3]
'quick_restart_no_lp': 3 [2,5]
Objective bounds Num
'initial_domain': 1
'objective_lb_search': 2
'objective_lb_search_no_lp': 4
'objective_shaving_search_no_lp': 1
For solutions, the first number is the number of solutions found by the
strategy, the second number is the range of the ranks of the solutions. The
value [1,7] indicates that the solutions found by the strategy have ranks
between 1 and 7. In this case, it means that the strategy no_lp found the best
and the worst solution.
For objective bounds, the number indicates how often the strategy contributed to
the best bound. For this example, it seems that the no_lp strategies are the
most successful. Note that for both cases, it is more interesting, which
strategies do not appear in the list.
In the search log, you can also see at which time which subsolver contributed something. This log also includes the incomplete and first solution subsolvers.
#1 0.01s best:43 next:[6,42] no_lp (fixed_bools=0/155)
#Bound 0.01s best:43 next:[7,42] objective_shaving_search_no_lp (vars=73 csts=120)
#2 0.01s best:33 next:[7,32] quick_restart_no_lp (fixed_bools=0/143)
#3 0.01s best:31 next:[7,30] quick_restart (fixed_bools=0/123)
#4 0.01s best:17 next:[7,16] quick_restart_no_lp (fixed_bools=2/143)
#5 0.01s best:16 next:[7,15] quick_restart_no_lp (fixed_bools=22/147)
#Bound 0.01s best:16 next:[8,15] objective_lb_search_no_lp
#6 0.01s best:15 next:[8,14] no_lp (fixed_bools=41/164)
#7 0.01s best:14 next:[8,13] no_lp (fixed_bools=42/164)
#Bound 0.01s best:14 next:[9,13] objective_lb_search
#Bound 0.02s best:14 next:[10,13] objective_lb_search_no_lp
#Bound 0.04s best:14 next:[11,13] objective_lb_search_no_lp
#Bound 0.06s best:14 next:[12,13] objective_lb_search
#Bound 0.25s best:14 next:[13,13] objective_lb_search_no_lp
#Model 0.26s var:125/126 constraints:162/162
#Model 2.24s var:124/126 constraints:160/162
#Model 2.58s var:123/126 constraints:158/162
#Model 2.91s var:121/126 constraints:157/162
#Model 2.95s var:120/126 constraints:155/162
#Model 2.97s var:109/126 constraints:140/162
#Model 2.98s var:103/126 constraints:135/162
#Done 2.98s objective_lb_search_no_lp
#Done 2.98s quick_restart_no_lp
#Model 2.98s var:66/126 constraints:91/162
Incomplete subsolvers are solvers that do not search the full problem space,
but work heuristically. Notable strategies are large neighborhood search (LNS)
and feasibility pumps. The first one tries to find a better solution by changing
only a few variables, the second one tries to make infeasible/incomplete
solutions feasible. You can also run only the incomplete subsolvers by setting
solver.parameters.use_lns_only = True, but this needs to be combined with a
time limit, as the incomplete subsolvers do not know when to stop.
First solution subsolvers are strategies that try to find a first solution as fast as possible. They are often used to warm up the solver and to get a first impression of the problem.
If you are interested in how Gurobi parallelizes its search, you can find a great video here. Ed Rothberg also explains the general opportunities and challenges of parallelizing a solver, making it also interesting for understanding the parallelization of CP-SAT.
 This section could need some help as there is the possibility that I am mixing up some of the strategies, or am drawing wrong connections. |
Importing/Exporting Models for Comparison on Different Hardware
If you want to compare the performance of different parallelization levels or different hardware, you can use the following code snippets to export a model. Instead of having to rebuild the model or share any code, you can then simply load the model on a different machine and run the solver.
from ortools.sat.python import cp_model
from google.protobuf import text_format
from pathlib import Path
def _detect_binary_mode(filename: str) -> bool:
if filename.endswith((".txt", ".pbtxt", ".pb.txt")):
return False
if filename.endswith((".pb", ".bin", ".proto.bin", ".dat")):
return True
raise ValueError(f"Unknown extension for file: {filename}")
def export_model(model: cp_model.CpModel, filename: str, binary: bool | None = None):
binary = _detect_binary_mode(filename) if binary is None else binary
if binary:
Path(filename).write_bytes(model.Proto().SerializeToString())
else:
Path(filename).write_text(text_format.MessageToString(model.Proto()))
def import_model(filename: str, binary: bool | None = None) -> cp_model.CpModel:
binary = _detect_binary_mode(filename) if binary is None else binary
model = cp_model.CpModel()
if binary:
model.Proto().ParseFromString(Path(filename).read_bytes())
else:
text_format.Parse(Path(filename).read_text(), model.Proto())
return model
The binary mode is more efficient and should be used for large models. The text mode is human-readable and can be easier shared and compared.
Hints
If you have a good intuition about how the solution might look—perhaps from solving a similar model or using a good heuristic—you can inform CP-SAT to incorporate this knowledge into its search. Some workers will try to follow these hints, which can significantly improve the solver’s performance if they are good. If the hints actually represent a feasible solution, the solver can use them to prune the search space of all branches that have worse bounds than the hints.
model.add_hint(x, 1) # Suggest that x will probably be 1
model.add_hint(y, 2) # Suggest that y will probably be 2
For more examples, refer to the official example. We will also see how to utilize hints for multi-objective optimization in the Coding Patterns chapter.
 Hints can significantly improve solver performance, especially if it struggles to find a good initial solution (as indicated in the logs). This practice is often called warm-starting the solver. You do not need to provide values for all auxiliary variables, but if you use integer variables to approximate continuous variables, it is beneficial to provide hints for these. CP-SAT may struggle with quickly completing the solution, and only completed solutions can be used for pruning the search space. If CP-SAT needs a long time to complete the solution from the hint, it may have wasted a lot of time in branches it could otherwise have pruned. |
To ensure your hints are correct, you can enable the following parameter, which will make CP-SAT throw an error if the hints are incorrect:
solver.parameters.debug_crash_on_bad_hint = True
If you suspect that your hints are not being utilized, it might indicate a logical error in your model or a bug in your code. This parameter can help diagnose such issues. However, this feature does not work reliably, so it should not be solely relied upon.
 In older versions of CP-SAT, hints could sometimes visibly slow down the solver, even if they were correct but not optimal. While this issue seems resolved in the latest versions, it is important to note that bad hints can still cause slowdowns by guiding the solver in the wrong direction. |
Often, you may need to explore the impact of forcing certain variables to specific values. To avoid copying the entire model multiple times to set the values of variables explicitly, you can also use hints to fix variables their hinted value with the following parameter:
solver.parameters.fix_variables_to_their_hinted_value = True
Hints can be cleared afterwards by calling model.clear_hints(), allowing you
to test other hints without duplicating the model. While you cannot add complex
expressions directly, fixing variables enables you to experiment with more
intricate constraints without model duplication. For temporary complex
constraints, model copying using model.CopyFrom may still be necessary, along
with variable copying.
You can also use this function to complete hints for auxiliary variables, which are often tedious and error-prone to set manually. To do so, invoke the function below before solving the model. Adjust the time limit based on the difficulty of completing the hint. If the values can be determined through simple propagation, even large models can be processed quickly.
def complete_hint(
model: cp_model.CpModel,
time_limit: float = 0.5,
):
"""
Completes the hint via a limited solve. Since CP-SAT only accepts complete hints,
performing this step can improve solver performance.
Args:
model: The CpModel object to update.
time_limit: Time limit for the solve (in seconds).
Notes:
This function performs a quick solve to deduce variable values.
If successful, it replaces any existing hint with a complete one.
If not successful, the model remains unchanged and a warning is issued.
"""
logging.info("Completing hint with a time limit of %d seconds", time_limit)
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit
solver.parameters.fix_variables_to_their_hinted_value = True
status = solver.solve(model)
logging.info(
"Automatically completing hint with status: %s", solver.status_name(status)
)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
# Clear the existing hint to avoid model invalidation.
model.clear_hints()
# Set a new complete hint using the solver result.
for i, _ in enumerate(model.proto.variables):
v_ = model.get_int_var_from_proto_index(i)
model.add_hint(v_, solver.value(v_))
logging.info(
"Hint successfully completed within time limit. Status: %s",
solver.status_name(status),
)
else:
logging.warning(
"Unable to complete hint within time limit. Status: %s",
solver.status_name(status),
)
 During presolve, the model is modified. For example, symmetries may be broken by prohibiting equivalent variations of the same solution. While such modifications can significantly improve performance by reducing the search space, they make it difficult to maintain the feasibility of hints, e.g., if a hint corresponds to a pruned variation. Unfortunately, CP-SAT has historically struggled to preserve the feasibility of hints through presolve. Although some issues have been resolved in earlier versions, I am still encountering this behavior in recent releases. As a workaround, you can instruct CP-SAT to retain all feasible solutions during presolve by setting: However, enabling this parameter may degrade solver performance. If you observe that hints become infeasible after presolve, you should experimentally determine whether maintaining feasible hints or doing the full presolve is more beneficial. |
Reinforcing the Model
For advanced users working with CP-SAT incrementally—i.e., modifying and solving the model multiple times—the following parameter may be of interest:
solver.parameters.fill_tightened_domains_in_response = True
When you remove the objective function and solve the feasibility version of your model, the solver returns tightened domains for the variables. This can significantly reduce the search space, improving solver performance, especially when solving the model multiple times with different objectives or additional constraints.
However, if the objective function is left in place, feasible solutions may be excluded from the search space. These solutions might become relevant if the objective or constraints are altered later.
Enabling this parameter does not modify the model itself; rather, it provides a list of tightened variable domains in the response object which you can then use in your model.
# Example after solving the model
for i, v in enumerate(self.model.proto.variables):
print(f"Tightened domain for variable {i} '{v.name}' is {solver.response_proto.tightened_variables[i].domain}")
Assumptions
Another way to explore the impact of forcing certain variables to specific values is by means of assumptions, which is a common feature in many SAT solvers. Unlike fixing hinted values, assumptions are restricted to boolean literals in CP-SAT.
b1 = model.new_bool_var("b1")
b2 = model.new_bool_var("b2")
b3 = model.new_bool_var("b3")
model.add_assumptions([b1, ~b2]) # assume b1=True, b2=False
model.add_assumption(b3) # assume b3=True (single literal)
# ... solve again and analyze ...
model.clear_assumptions() # clear all assumptions
 While incremental SAT solvers can reuse learned clauses from previous runs despite changes in assumptions, CP-SAT does not support this feature. Its solver is stateless and always starts from scratch. |
While assumptions can be used to explore different assignments of Boolean
variables without reconstructing the model, CP-SAT offers a more powerful
feature: the extraction of unsatisfiable cores from infeasible models. This
capability is particularly useful for model debugging. By enabling constraints
conditionally using only_enforce_if(b) and adding b as an assumption, one
can isolate sources of infeasibility. If the model proves infeasible, CP-SAT can
return a minimal subset of the assumptions, and thus the corresponding
constraints, that lead to the conflict.
Consider the following example. Suppose we have a model with three integer variables \( x \), \( y \), and \( z \), along with the following constraints:
- \( x + y \leq 4 \)
- \( x + z \leq 2 \)
- \( z \geq 4 \)
Since all variables are non-negative integers, this model is clearly infeasible
due to the incompatibility between constraints (2) and (3). When dealing with
larger models, identifying the source of infeasibility can be challenging.
However, by using assumptions in conjunction with
sufficient_assumptions_for_infeasibility, CP-SAT can automatically identify
which constraints are responsible.
from ortools.sat.python import cp_model
model = cp_model.CpModel()
# Integer variables
x = model.new_int_var(0, 100, 'x')
y = model.new_int_var(0, 100, 'y')
z = model.new_int_var(0, 100, 'z')
# Constraints
indicator_1 = model.new_bool_var('Indicator 1: x + y <= 4')
model.add(x + y <= 4).only_enforce_if(indicator_1)
indicator_2 = model.new_bool_var('Indicator 2: x + z <= 2')
model.add(x + z <= 2).only_enforce_if(indicator_2)
indicator_3 = model.new_bool_var('Indicator 3: z >= 4')
model.add(z >= 4).only_enforce_if(indicator_3)
# Assumptions
model.add_assumptions([indicator_1, indicator_2, indicator_3])
# Solve
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.INFEASIBLE
print("Minimal unsat core:")
for var_index in solver.sufficient_assumptions_for_infeasibility():
print(f"{var_index}: '{model.proto.variables[var_index].name}'")
This produces the following output:
Minimal unsat core:
4: 'Indicator 2: x + z <= 2'
5: 'Indicator 3: z >= 4'
Unfortunately, not all constraints in CP-SAT support reification. However, lower-level constraints, where infeasibilities are most likely to occur, typically do. For higher-level constraints, workarounds may exist to express them in a reifiable form.
 You can find more information on this in the CPMpy documentation, a modelling library that also supports CP-SAT as backend. |
Presolve
The CP-SAT solver includes a presolve step that simplifies the model before solving it. This step can significantly reduce the search space and enhance performance. However, presolve can be time-consuming, particularly for large models. If your model is relatively simple—meaning there are few genuinely challenging decisions for CP-SAT to make—and you notice that presolve is taking a long time while the search itself is fast, you might consider reducing the presolve effort.
For example, you can disable presolve entirely with:
solver.parameters.cp_model_presolve = False
However, this approach might be too drastic, so you may prefer to limit presolve rather than disabling it completely.
To reduce the number of presolve iterations, you can use:
solver.parameters.max_presolve_iterations = 3
You can also limit specific presolve techniques. For instance, you can constrain the time or intensity of probing, which is a technique that tries to fix variables and observe the outcome. Although probing can be powerful, it is also time-intensive.
solver.parameters.cp_model_probing_level = 1
solver.parameters.presolve_probing_deterministic_time_limit = 5
There are additional parameters available to control presolve. Before making adjustments, I recommend reviewing the solver log to identify which aspects of presolve are causing long runtimes.
Keep in mind that reducing presolve increases the risk of failing to solve more complex models. Ensure that you are not sacrificing performance on more challenging instances just to speed up simpler cases.
Adding Your Own Subsolver to the Portfolio
As we have seen, CP-SAT uses a portfolio of different subsolvers, each configured with varying settings (e.g., different levels of linearization) to solve the model. You can also define your own subsolver with a specific configuration. It is important not to modify the parameters at the top level, as this would affect all subsolvers, including the LNS-workers. Doing so could disrupt the balance of the portfolio, potentially activating costly techniques for the LNS-workers, which could slow them down to the point of being ineffective. Additionally, you risk creating a default subsolver incompatible with your model - such as one that requires an objective function - causing CP-SAT to exclude most or all subsolvers from the portfolio, resulting in a solver that is either inefficient or nonfunctional.
For example, in packing problems, certain expensive propagation techniques can significantly speed up the search but can also drastically slow it down if misused. To handle this, you can add a single subsolver that applies these techniques. If the parameters do not help, only one worker will be slowed down, while the rest of the portfolio remains unaffected. However, if the parameters are beneficial, that worker can share its solutions and (variable) bounds with the rest of the portfolio, boosting overall performance.
Here is how you can define and add a custom subsolver:
from ortools.sat import sat_parameters_pb2
packing_subsolver = sat_parameters_pb2.SatParameters()
packing_subsolver.name = "MyPackingSubsolver"
packing_subsolver.use_area_energetic_reasoning_in_no_overlap_2d = True
packing_subsolver.use_energetic_reasoning_in_no_overlap_2d = True
packing_subsolver.use_timetabling_in_no_overlap_2d = True
packing_subsolver.max_pairs_pairwise_reasoning_in_no_overlap_2d = 5_000
# Add the subsolver to the portfolio
solver.parameters.subsolver_params.append(packing_subsolver) # Define the subsolver
solver.parameters.extra_subsolvers.append(
packing_subsolver.name
) # Activate the subsolver
After adding the subsolver, you can check the log to verify that it is included in the list of active subsolvers. If it is not shown, you probably used parameters incompatible with the model, causing the subsolver to be excluded.
8 full problem subsolvers: [MyPackingSubsolver, default_lp, max_lp, no_lp, probing, probing_max_lp, quick_restart, quick_restart_no_lp]
If you want to find out how the existing subsolvers are configured, you can check out the cp_model_search.cc file in the OR-Tools repository.
 You can also overwrite the parameters of an existing subsolver by using the same name. Only the parameters you explicitly change will be updated, while the others will remain as they are. Additionally, you can add multiple subsolvers to the portfolio, but keep in mind that doing so might push some predefined subsolvers out of the portfolio if there are not enough workers available. |
Decision Strategy
In the end of this section, a more advanced parameter that looks interesting for
advanced users as it gives some insights into the search algorithm. It can be
useful in combination with solver.parameters.enumerate_all_solutions = True to
specify the order in which all solutions are iterated. It can also have some
impact on the search performance for normal optimization, but this is often hard
to predict, thus, you should leave the following parameters unless you have a
good reason to change them.
We can tell CP-SAT, how to branch (or make a decision) whenever it can no longer deduce anything via propagation. For this, we need to provide a list of the variables (order may be important for some strategies), define which variable should be selected next (fixed variables are automatically skipped), and define which value should be probed.
We have the following options for variable selection:
CHOOSE_FIRST: the first not-fixed variable in the list.CHOOSE_LOWEST_MIN: the variable that could (potentially) take the lowest value.CHOOSE_HIGHEST_MAX: the variable that could (potentially) take the highest value.CHOOSE_MIN_DOMAIN_SIZE: the variable that has the fewest feasible assignments.CHOOSE_MAX_DOMAIN_SIZE: the variable the has the most feasible assignments.
For the value/domain strategy, we have the options:
SELECT_MIN_VALUE: try to assign the smallest value.SELECT_MAX_VALUE: try to assign the largest value.SELECT_LOWER_HALF: branch to the lower half.SELECT_UPPER_HALF: branch to the upper half.SELECT_MEDIAN_VALUE: try to assign the median value.
model.add_decision_strategy([x], cp_model.CHOOSE_FIRST, cp_model.SELECT_MIN_VALUE)
# your can force CP-SAT to follow this strategy exactly
solver.parameters.search_branching = cp_model.FIXED_SEARCH
For example for coloring (with
integer representation of the color), we could order the variables by decreasing
neighborhood size (CHOOSE_FIRST) and then always try to assign the lowest
color (SELECT_MIN_VALUE). This strategy should perform an implicit
kernelization, because if we need at least \( k \) colors, the vertices with less
than \( k \) neighbors are trivial (and they would not be relevant for any
conflict). Thus, by putting them at the end of the list, CP-SAT will only
consider them once the vertices with higher degree could be colored without any
conflict (and then the vertices with lower degree will, too). Another strategy
may be to use CHOOSE_LOWEST_MIN to always select the vertex that has the
lowest color available. Whether this will actually help, has to be evaluated:
CP-SAT will probably notice by itself which vertices are the critical ones after
some conflicts.
 I played around a little with selecting a manual search strategy. But even for the coloring, where this may even seem smart, it only gave an advantage for a bad model and after improving the model by symmetry breaking, it performed worse. Further, I assume that CP-SAT can learn the best strategy (Gurobi does such a thing, too) much better dynamically on its own. |
The CP-SAT Primer is maintained by Dominik Krupke at the Algorithms Division, TU Braunschweig, and is licensed under the CC BY 4.0 license. Contributions are welcome.
If you find the primer helpful, consider leaving a ⭐ on GitHub (574⭐) or sharing your feedback/experience. Your support helps improve and sustain this free resource.

